两级运放的自动化设计思路

前言

两级运放是一个比较常见的模块。其中以5管+共源级最为简单，一般在中等增益时还是适用的。

基本概念

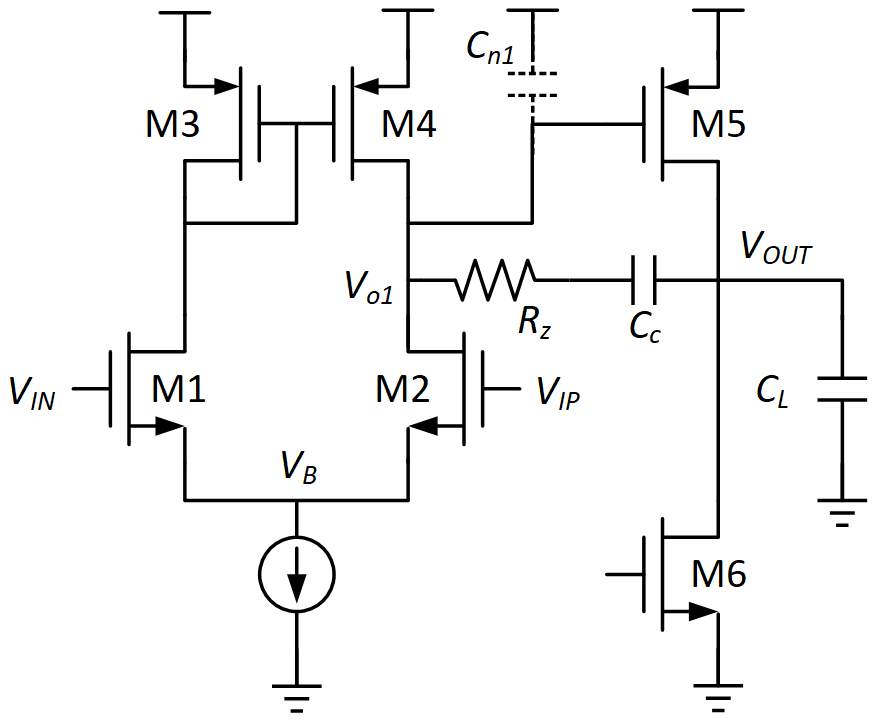
图1 两级运放基本结构

如图1所示，Vout处会有一个较大的负载电容C L ，为了驱动这个大电容，M5需要较大的尺寸，导致M1、M2、M3、M4构成的第一级会看到很大的负载，这样第一级（以后简称S1）的极点和第二级（以后简称S2）的极点相距很近，接成闭环后运放很不稳定，甚至振荡。

为此，加入电容C c ，由于密勒效应，S1输出节点形成一个很大的等效电容负载，极点频率变低。对于S2，Cc跨接在M5两端，形成了漏到栅的负反馈，减小了S2等效的输出电阻，S2的极点变大。这就是所谓的极点分裂。

详细的理论推导此处不再描述，直接上张老师(张鸿-西安交大）课件上的结论：（A1为第一级的增益，A2为第二级的增益，gmx代表标号为x的MOS管的跨导，其余类似） 主极点的角频率为 式(1) ：

非主极点的角频率为 式(2) ：

其中Cn1是VO1节点对交流地的总寄生电容。

对于两级运放这样一个二阶系统，为了保证闭环后（假定反馈系数为1）系统是稳定的，ωnd和GBW应具有足够的距离来保持足够的相位裕度。以60°相位裕度为例，此时GBW=ω d ×(A 1 ×A 2 )=ω d ×(g m1 (r o2 ||r o4 )×A 2 )=g m1 /C c ，ω nd ≈1.5GBW。

寄生导致反复迭代

对于S2，其输出端的寄生电容会增大VOUT节点的等效负载，因此一般手算之后需要提高S2的尺寸来保证ω nd ；另一方面，M5栅极到“交流地”的寄生会降低Cc的负反馈效果而降低ω nd ，所以需要反复迭代。

对于S1，理论上的负载电容为A 2 ×C c ；事实上，Cgd5也是密勒电容的一部分，C gs5 +Cgb5也增加了一部分负载。这样，VO1节点的等效负载为A 2 ×(C c +C gd5 )+C gs5 +C gb5 ，式(1)重写为：

在S1的输出端，M2和M4的漏端寄生电容也会降低Cc的反馈效果，拉低ω nd 。

整体思路

给定负载、电流、带宽、增益4个参数，且 假设S2输入级的DC值已经根据输出摆幅确定好 ，整体运行思路如下：

• A: 设定S2的初始增益，求解S2的尺寸，读取S2的各个寄生和总电流；
• B: 计算S1的可用电流，将S2的寄生折算为S1的负载，求解S1尺寸；
• C: 迭代优化S1输出节点的寄生电容；
• D: S1+S2拼接，扫描调零电阻。

Step1：确定S2

当S2的增益A2和M5的DC偏置点确定之后，假定S1输出点寄生C node =1pF（Cnode主要由M2和M4的漏端电容构成，后面会再提到）：

python调用hspice扫描M5的L，获取“当g m5 ×r out5 =2×A 2 ”的L值，获取此时M5的r out5 ×id5；

继续扫描M6的L，获取“r out6 ×i d6 =r out5 ×i d5 ”的L值（这个方法在求解S1时也会用到），那么此时所选取的M6的沟长，能使M6在流过和M5相同电流的情况下，得到和M5相同的输出电阻。此时，hspice扫描得到gm5和C gs5 +C gb5 ，C gd5 ，C ds5 +C db5 +Cdd6的比例关系，ωnd的表达式参考拉扎维式10.24重写如下 式(3) ：

其中ωnd的目标值为1.5GBW，RL是S2的输出电阻，值为A 2 /g m5 。

C mil 、C Lx 、Ce分别为考虑S2寄生电容后的总密勒值，总负载值和VO1节点的总寄生值（包含C node ），这3个变量均由1个固定值+1个与gm成正比的值组成。

直接求解式(3)（化简后是一个一元二次方程），获取gm5的最终值g m_target 。gm_target除以当前gm5的值，即可得到M5的finger数；同时也可得到S2预期的电流值cur2。

式(3)可能无解或最终求出一个很大的cur2，此时说明Cc太小，寄生对极点分裂的削弱作用过大，迭代Cc重新求解（这部分可由程序自动进行）。

有可能通过一个很大的Cc来使(3)具有一个合适的解，但此时S1的等效负载会很大，导致S1无解，此时说明当前的增益分配不合理，调整S2的增益，重新迭代。

Step2: 确定S1

如前所述，S2解出之后，需要回传一些参数：

一是S2的预期电流cur2，总电流-cur2即为S1可接受的电流；

二是S2的C gd5 、Cgs5和C gb5 ，A 2 (C gd5 +C c )+C gs5 +Cgb5是第一级总的负载电容。在这个负载电容下，S1所产生的主极点频率为ω d =GBW/(A 1 ×A 2 )，结合式(1)可以确定S1的输出电阻；S1增益为A 1 ，所以S1预期的跨导gm_s1可以确定.

相比于S2，S1多出了一个需要优化的变量，源端电压V B 。对于N管，VB越大，Vod越小，g m /id越大；但同时需要的管子面积可能也越大，带来很大的寄生电容。

当VB较小时，实现同样的gm会需要更大的电流，但是总面积可能减小；也有可能增大，因为Vgs较大时，MOS管实现相同的本征增益可能需要更大的L。

VB大了不行，小了也不行，还是让代码直接迭代吧。

首先，扫描一个基本管子的V th ，进而确定VB使Vod在300mV左右，VB从此时开始迭代。

从180n10u扫描MOS管的增益，得出合适的L（记为L1）后计算其g m /i d ，满足要求则扩展MOS管的finger，达到gm_s1的跨导；否则增加V B ，直至求出同时满足增益和g m /id的M1/M2尺寸；按照前述r out *id~相等的原则确定M3/M4的尺寸。

计算此时M2和M4带来的寄生电容C par1 ，将L的求解范围设为（180n ~ L1 - 50n），继续求解。当解出的寄生电容比上次寄生电容大，或者无解时，停止迭代。此时即解出了S1的尺寸参数，且此时S1在VO1节点产生的寄生电容是最小的。

如果一开始即设置了一个合适的C node ，最后解出的S1输出点的寄生电容小于这个预设值，此时迭代已经完成了，电路拼接之后即可实现预期的带宽和相位裕度。

如果解出的S1输出寄生大于预设的C node ，重新标定Cnode并再次先后求解S2和S1即可。

注意，上述求解过程中为了方便程序迭代，VB是一个固定电压，全差分电路时这样是可以的，在差分转单端电路中，VB并不能按照固定电压处理，需要将VB换成一个MOS电流源。

Step3: 调零电阻Rz

对调零电阻带来的影响进行详细推导需要大量篇幅，此处直接迭代Rz并根据GBW和相位裕度更新，得到一个满足要求的解即可。

题外话

两级运放如果直接采用5管，也很难做到较高增益。当S1增益很大时，其输出点VO1的寄生电容很高，会导致S2的功耗很高甚至是式(3)无解；所以高增益时还是共源共栅+两级更好一点，这样VO1节点的寄生电容相对较小（个人观点）。

考虑到Rz的调节作用，S2的设计可以更激进一些。例如为了满足60°相位裕度，ωnd的目标从1.5GBW下降到1GBW，最后用Rz调出正确结果。