

STA分析—延迟计算
电子说
描述
引言
从上篇文章,我们可以很明显的看出STA的两大因素,一个是延迟计算,一个是约束检查。STA最基本的工作之一就是检查路径延迟是否符合约束。
本篇文章主要讲延迟计算。约束检查在后续篇章讲。
路径延迟组成
路径延迟(path delay)由单元延迟(cell delay)和线延迟(wire delay)组成:
path delay = 所有cell delay + 所有wire delay。
上篇文章中的计算式:
D(FFL1->FFC1)
= D(FFL1CP2Q) + D(C1) ~ ~ + D(UNAND1) + D(C2) + D(UINV2) + D(C3) + D(UINV3) + D(C4) + D(UINV4) + D(C5)
= 0.1 + 0.1 + 0.1 + 0.05 + 0.1 + 0.05 + 0.05 + 0.05 + 0.1 + 0.05
= 0.75ns
其中,D(FFL1->FFC1) 是从起始单元FFL1到终点单元FFC1的path delay,D(FFL1CP2Q)=0.1ns 是FFL1时序单元的cell delay,D(UNAND1)是UNAND1组合逻辑单元的cell delay……,D(C1)是线网C1的wire delay,D(C2)是线网C2的wire delay……
请注意,不管是path delay,还是cell delay,都有明确具体的pin起点和终点,如D(UNAND1)指的是cell UNAND1的A pin到Z pin的延迟。
Cell delay
先讲Cell delay的计算
我们将图一里反相器UINV2的内部MOS电路画出来,来理解cell延迟是如何发生的:

图一 逻辑电路图(含BC工作条件下的延迟信息)
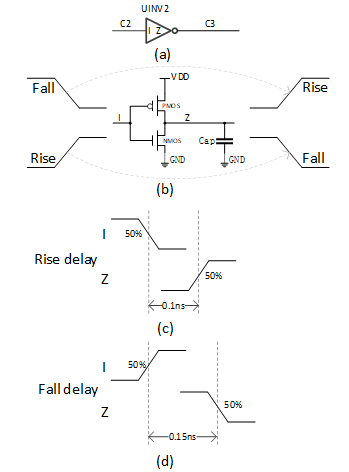
**图二 **反相器逻辑图
如上图所示,cell delay分 rise delay和fall delay 。
Rise fall是按照cell的输出翻转(transition)方向来定义的。考虑输入是fall transition,输出是rise transition的情形。 一开始,UINV2的输入pin I上的电平是高电平,此时PMOS处于截止状态,NMOS管处于导通状态,电容的上端通过NMOS管与地接通。 只要这个状态持续足够长,电容上的电会被放完,电放完时,UINV2单元的输出pin Z处于低电平状态。 接下来,I端开始Fall transition,到达PMOS的阈值电压后,PMOS管完全导通, 电源通过PMOS管的channel向Cap充电,由于电容的存在,Z端电平出现一个缓慢上升的过程。
如图二(c)所示,从I端的fall transion的50%电压处,到Z端的rise transion的50%处,其时间差(0.1ns)即是该反相器的I端到Z端的rise delay。同样,从图八(d)可见,反相器的I端到Z端的fall delay是0.15ns。我们注意到rise delay和fall delay不相等,这是因为PMOS和NMOS导通后的channel电阻不一样,所以充放电速度不一样,表现出来即是delay不一样。
实际的STA过程,是通过查找表的方式来获得cell delay的。 如下图,在NLDM库里输入input transition和output capacitance,得到rise delay或者fall delay值:

Wire delay
从UINV2的Z输出端到UINV3的I输入端之间是由金属线连接起来的, wire存在寄生的电容电阻 。
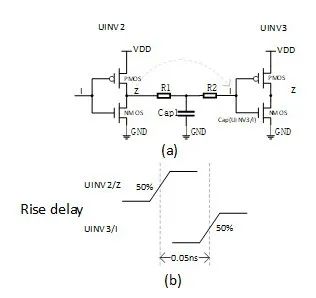
**图三 **线延迟
**wire delay = R1*Cap1 + (R1+R2)*Cap(UINV3/I)。**
一般情况, UINV2到UINV3之间的wire寄生参数可以用分布式RC树来建模,作为分布式RC数的简化模型,有T模型和Pi模型。 这里我们使用了简化的T模型来建模和计算RC延迟。
现在,我们回头再来看一下上面的path delay,它并没有指出其delay是由起点处的rise transition还是fall transition经过路径传播引起的,所以严格来说,计算式的正确性是值得怀疑的。
有了上述知识后,我们重新标注了各个cell和wire的延迟,如图十所示,“R:0.1”代表rise delay是0.1ns,“F:0.1”代表fall delay是0.1ns。同时,我们从这篇文章开始,将时钟树也纳入考虑范围,因此,时钟树上的cell delay和wire delay也标识出来了。
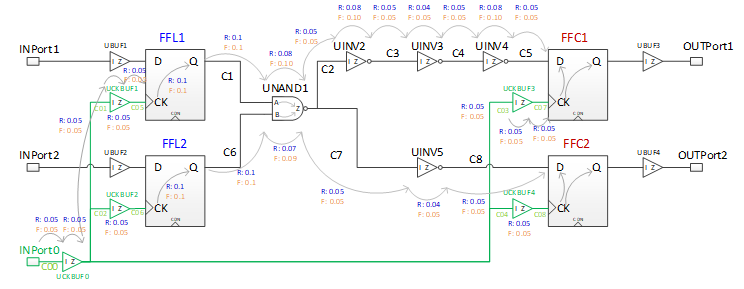
图四 逻辑电路图(含BC****工作条件下的延迟信息)
很明显,到FFC1存在两条逻辑路径,一条是从FFL1出发的路径,一条是从FFL2出发的。从FFL1到FFC1的path delay有rise delay和fall delay,从FFL2到FFC1的path delay也有rise delay和fall delay,所以到FFC1的path delay总共有22 = 4条,即。同理,到FFC2的path delay也总共有22 = 4条。
小结
STA工具会计算这4条逻辑路径上的总共8个path delay。然后与时序约束值做运算,判断是否满足约束。
想必看到这里,读者童鞋会对路径延迟有一个大概的了解。下一篇,我们介绍如何对这些路径做setup、hold时序检查,以及相关的STA概念。
-
延迟子函数怎么计算2014-07-15 2572
-
为什么STA321MPL上会有5个样本延迟?2019-07-24 1257
-
如何计算延迟和吞吐量?2020-03-19 2363
-
如何使用AOCV做STA分析2021-02-01 3143
-
静态时序分析STA的优点以及缺点分别有哪些呢2021-11-02 2249
-
esp32在STA模式,ping延迟大,丢包多怎么解决?2023-02-16 1015
-
STA7056.pdf2011-09-19 1119
-
时序分析基本概念——STA概述简析2017-12-14 30872
-
基本的时序约束和STA操作流程2021-08-10 6571
-
山西大学选购我司HS-STA-002同步热分析仪2023-02-23 1554
-
STA-0.静态时序分析概述2023-06-27 2009
-
STA分析-从一个案例开始2023-07-05 3147
-
sta同步热分析仪2023-08-15 1498
-
镇江安恬新材料有限公司选购我司HS-STA-002同步热分析仪2024-08-07 705
-
边缘计算对网络延迟的影响2024-10-24 1947
全部0条评论

快来发表一下你的评论吧 !

