设计大规模并行哈希图时的几个重要考虑事项

数十年的计算机科学史致力于设计有效存储和检索信息的解决方案。哈希图（或哈希表）是一种流行的信息存储数据结构，因为它对元素的插入和检索具有摊销、恒定的时间保证。

然而，尽管哈希图很流行，但很少在 GPU 加速计算的上下文中讨论哈希图。虽然 GPU 以其大量线程和计算能力而闻名，但其极高的内存带宽使许多数据结构（如哈希图）得以加速。

这篇文章介绍了哈希图的基本原理，以及它们的内存访问模式如何使其非常适合 GPU 加速。我们将介绍 cuCollections ，这是一个用于并发数据结构（包括哈希图）的新的开源 CUDA C ++库。

最后，如果您对在应用程序中使用 GPU 加速哈希映射感兴趣，我们将提供多列关系连接算法的示例实现。 RAPIDS cuDF 集成了 GPU 哈希图，这有助于实现 数据科学工作负载的惊人加速 。要了解更多信息，请参阅 GitHub 上的 rapidsai/cudf 和 使用 Dask 和 RAPIDS 为自然语言处理加速 TF-IDF 。

您还可以将 cuCollections 用于表格数据处理之外的许多用例，例如推荐系统、流压缩、图形算法、基因组学和稀疏线性代数操作。

哈希图基础知识

哈希映射是 associative 容器，这意味着它们存储 key – value 对，其中 key 映射到关联的 value ，从而通过查找其键来检索值。例如，您可以使用哈希图来实现电话簿，方法是使用个人的姓名作为密钥，将其电话号码作为关联值。

哈希映射与其他关联容器的不同之处在于，插入或检索等操作的平均成本是恒定的。 std::map 在 C ++标准模板库中不是哈希表，但通常实现为二进制搜索树。 std::unordered_map 更类似于与此讨论相关的哈希表类型。在本文中，哈希表和哈希图之间没有区别。这两个术语将在整个过程中互换使用。

单值与多值比较

讨论哈希表时的一个重要区别是是否允许重复键。单值哈希表或哈希映射要求键是唯一的（例如，std::unordered_map），而多值哈希表和哈希多映射允许重复键（例如，std::unordered_multimap）。

使用电话簿类比，后者指的是一个人可以拥有多个电话号码的情况。例如，电话簿可以具有 (k=Alice, v=408-555-0148) 和具有另一个值 (k=Alice, v=408-555-3847) 的重复密钥。

存储和检索

从概念上讲，哈希映射由一个桶数组组成，其中每个桶可以包含一个或多个键值对。要在映射中插入新的对，将向键应用哈希函数以生成哈希值。然后使用该哈希值选择其中一个桶。如果存储桶可用，则该对存储在该存储桶中。

例如，要插入对 (Alice, 408-555-0148) ，您对键 hash(Alice)=4, 进行散列以获取其散列值，并选择位置 4 处的存储桶来存储对。稍后，要检索与 Alice 关联的值，可以使用相同的哈希函数 hash(Alice), 再次选择位置 4 处的存储桶并检索先前存储的值。

哈希冲突

如果表中桶的数量等于可能的键的数量，则可以使用哈希桶和键之间的一对一关系，其中每个键正好映射到表中的一个桶。

然而，这在大多数情况下是不切实际的，因为潜在密钥的数量事先不知道，或者为每个密钥保留存储桶所需的存储将超过可用的存储容量。想象一下，如果你的电话簿必须为宇宙中每个可能的名字保留一个条目！

因此，哈希函数通常是不完美的，并可能导致哈希冲突，其中两个不同的键映射到相同的哈希值（图 1 ）。好的哈希函数寻求最小化冲突的可能性，但在大多数情况下它们是不可避免的。

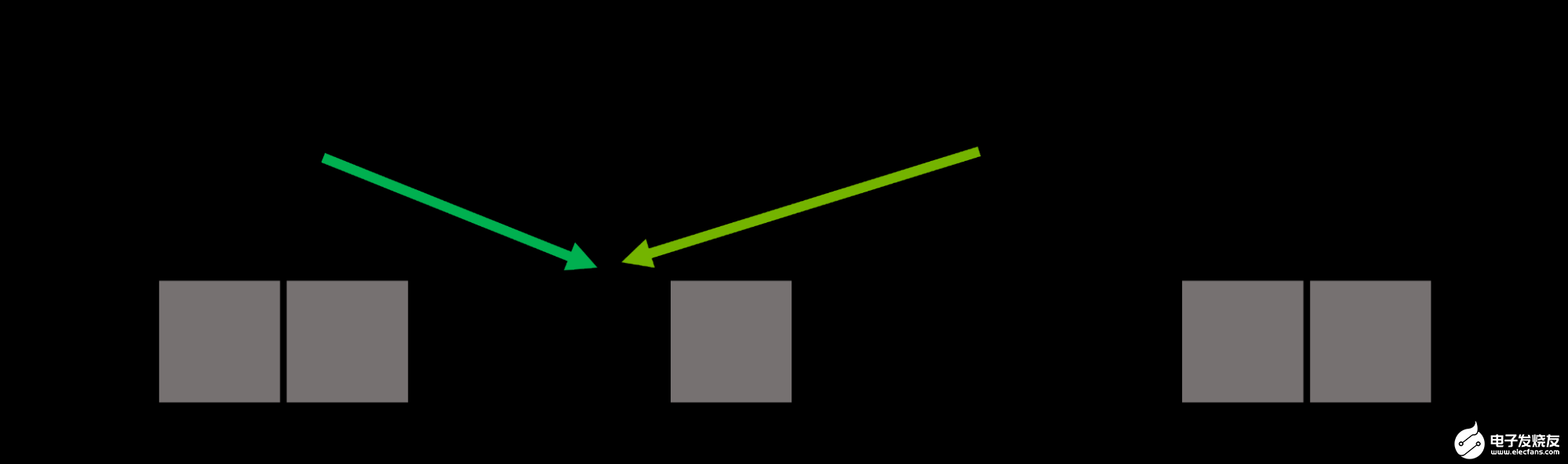图 1 。两个不同的键， Alice 和 Bob ，具有相同的哈希值，导致桶 4 处的哈希冲突

打开寻址

在文献中可以找到许多解决哈希冲突的策略，但本文重点介绍了一种名为 open addressing with linear probing 的策略。

开放寻址哈希表使用内存中的连续存储桶数组。使用线性探测，如果在位置 i, 处遇到已占用的铲斗，则移动到下一个相邻位置 i+1 。如果这个桶也被占用了，你就转到 i+2, ，依此类推。当你到达最后一个桶时，你就绕回到开头。这个所谓的 probing scheme 对于每个密钥都是确定性的（图 2 ）。

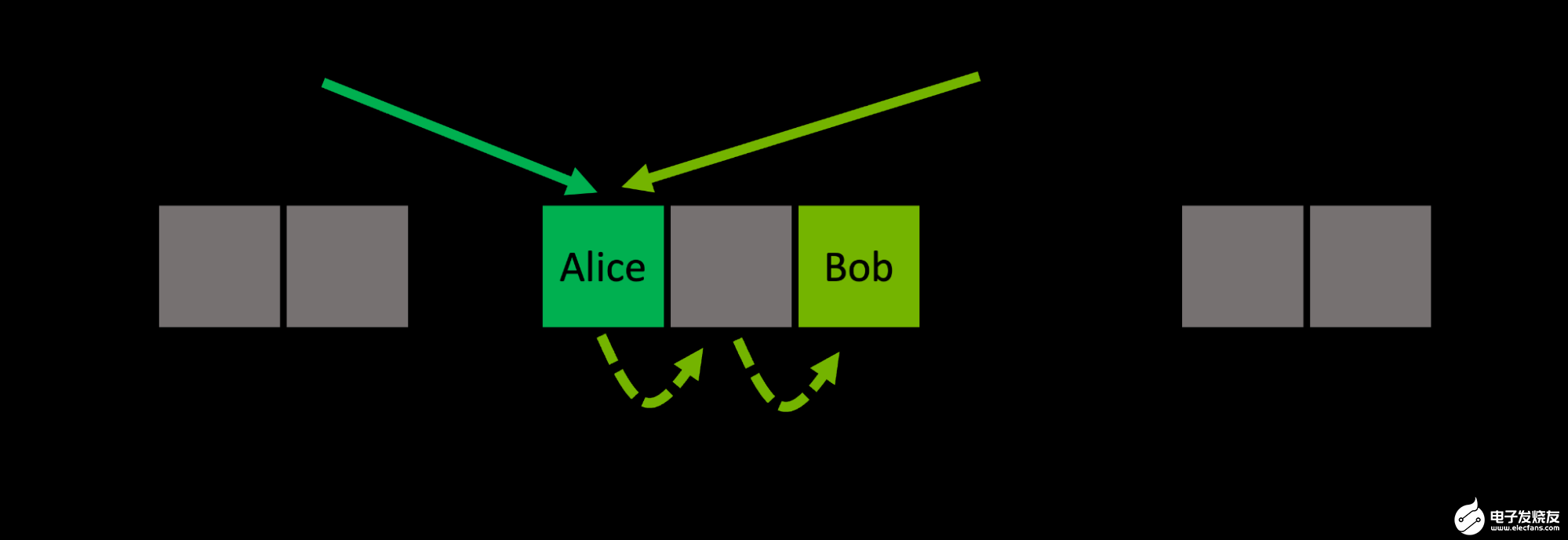图 2 :开放寻址通过探测方案在不同位置存储冲突条目，探测方案以确定性顺序遍历一系列备选存储桶

这种方法具有缓存效率，因为它访问内存中的连续位置。如果 负载因子（已填充的存储桶与总存储桶的比率）较高，则可能会导致性能下降，因为这会导致额外的内存读取。

从地图中检索关键字 Bob 的工作方式相同：从位置 hash(Bob)=4 开始遵循关键字的探测顺序，直到在位置 6 找到所需的桶。如果在给定键的探测序列中的任何一点上遇到空桶，则知道所查询的键不在映射中。

随机存储器访问

精心设计的哈希函数通过最大化哈希任意两个键将导致不同哈希值的可能性来最小化冲突次数。这意味着对于任何给定的两个键，它们对应的桶可能位于不同的内存位置。

因此，大多数哈希表操作的内存访问模式实际上是随机的。为了理解哈希表的性能，了解随机内存访问的性能非常重要。

表 1 比较了理论峰值带宽与在现代 GPU s 和 GPU s 上通过 GUPS benchmark 测量的随机 64 位读取的实现带宽。

Chip (memory)	Theoretical peak bandwidth (GB/s)	Measured random 64-bit read bandwidth (GB/s)
Intel Xeon Platinum 8360Y (DDR4-3200, 8 channels)	204	15
NVIDIA A100-80GB-SXM (HBM2e)	2039	141
NVIDIA H100-80GB-SXM (HBM3)	3352	256

表 1 . 带宽计算为访问大小乘以访问次数除以时间

如果您有兴趣在系统上运行 GUPS GPU 基准测试，请参阅 NVIDIA developer blog code samples GitHub 存储库。您可以访问 ParRes/Kernels GitHub 存储库中的 CPU 代码。

如您所见，随机内存访问大约比理论峰值带宽慢 10 倍。这是因为内存子系统针对顺序访问进行了优化。更重要的是， NVIDIA GPU s 的随机访问吞吐量比现代 CPU s 的高一个数量级。这些结果表明，性能最好的 CPU 哈希表可能比性能最好的 GPU 哈希表慢一个数量级。

GPU 哈希图实现

随机内存访问在哈希表实现中是不可避免的， GPU 在随机访问方面优于 CPU 。这很有希望，因为它暗示 GPU 应该擅长哈希表操作。为了测试这一理论，本节讨论 GPU 哈希表的实现和优化，并将性能与 CPU 实现进行比较。

目标不是开发一个标准 C ++容器（如std::unordered_map）的替代品，而是专注于实现一个哈希表，该哈希表适用于 GPU 加速应用程序中出现的大规模并行、高吞吐量问题。

本示例使用以下简化假设：

表的容量是固定的，不能添加超出初始容量的其他键值对

需要将其中一个可能的键值设置为哨兵值，以指示空桶

键和值类型的大小之和必须小于或等于 8 个字节

插入后不能删除键值对

请注意，这些不是基本的限制，可以通过 cuCollections 库中提供的更高级的实现来克服。

首先，示例哈希表使用开放寻址，由一组桶组成。每个存储桶可以保存一个键 – 值对，并使用键/值标记进行初始化，以表示当前为空。对于冲突解决，使用线性探测 。

GPU 加速哈希表需要支持来自多个线程的并发更新，例如，如果两个线程试图在同一位置插入，则需要采取步骤避免数据竞争。为了避免昂贵的锁定，示例哈希表通过 cuda::std::atomic 其中每个铲斗定义为cuda::std::atomic>。

为了插入新的密钥，实现根据其哈希值计算第一个存储桶，并执行原子比较和交换操作，期望存储桶中的密钥等于empty_sentinel。如果是，则插槽为空，插入成功。否则，它前进到下一个桶，直到最终找到一个空桶。

下面的代码显示了哈希表插入函数的简化版本。

 

__device__ bool insert(Key k, Value v) {
// get initial probing position from the hash value of the key
auto i = hash(k) % capacity;
while (true) {
  // load the content of the bucket at the current probe position
  auto [old_k, old_v] = buckets[i].load(memory_order_relaxed);
  // if the bucket is empty we can attempt to insert the pair
  if (old_k == empty_sentinel) {
    // try to atomically replace the current content of the bucket with the input pair
    bool success = buckets[i].compare_exchange_strong(
                    {old_k, old_v}, {k,v}, memory_order_relaxed);
    if (success) {
      // store was successful
      return true;
    }
  } else if (old_k == k) {
    // input key is already present in the map
    return false;
  }
  // if the bucket was already occupied move to the next (linear) probing position
  // using the modulo operator to wrap back around to the beginning if we     
  // go beyond the capacity
  i = ++i % capacity;
}
}

 

在映射中查找特定键的关联值的方式类似。沿钥匙探测顺序检查每个位置，直到找到包含所需钥匙的存储桶或空存储桶，表明钥匙无法驻留在表中。

合作团体

最初，为每个输入元素分配一个工作线程似乎是一个合理的比率。但是，请考虑以下事项：

输入中的相邻键与其在存储器中的相关探测位置之间没有关系。这意味着扭曲中的每个线程都可能访问哈希图的完全不同的区域。在最坏的情况下，每个探测步骤需要从全局内存中的 32 个不同位置加载每个扭曲。（回想随机内存访问。）

利用线性探测，每个线程可以从其初始探测位置开始访问多个相邻桶。这种本地访问模式将允许使用单个联合负载预取多个探测位置，不幸的是，这无法通过单个线程实现。

我们能做得更好吗？对 CUDA cooperative groups 模型可以轻松地重新配置工作分配的粒度。每个输入元素不使用单个 CUDA 线程，而是将一个元素分配给同一经线内的一组连续线程。

对于给定的输入键，不是按顺序遍历其关联的探测序列，而是用单个合并负载预取多个相邻桶的窗口。然后，该组使用有效的ballot和shuffle内部函数协同确定窗口内的候选桶。

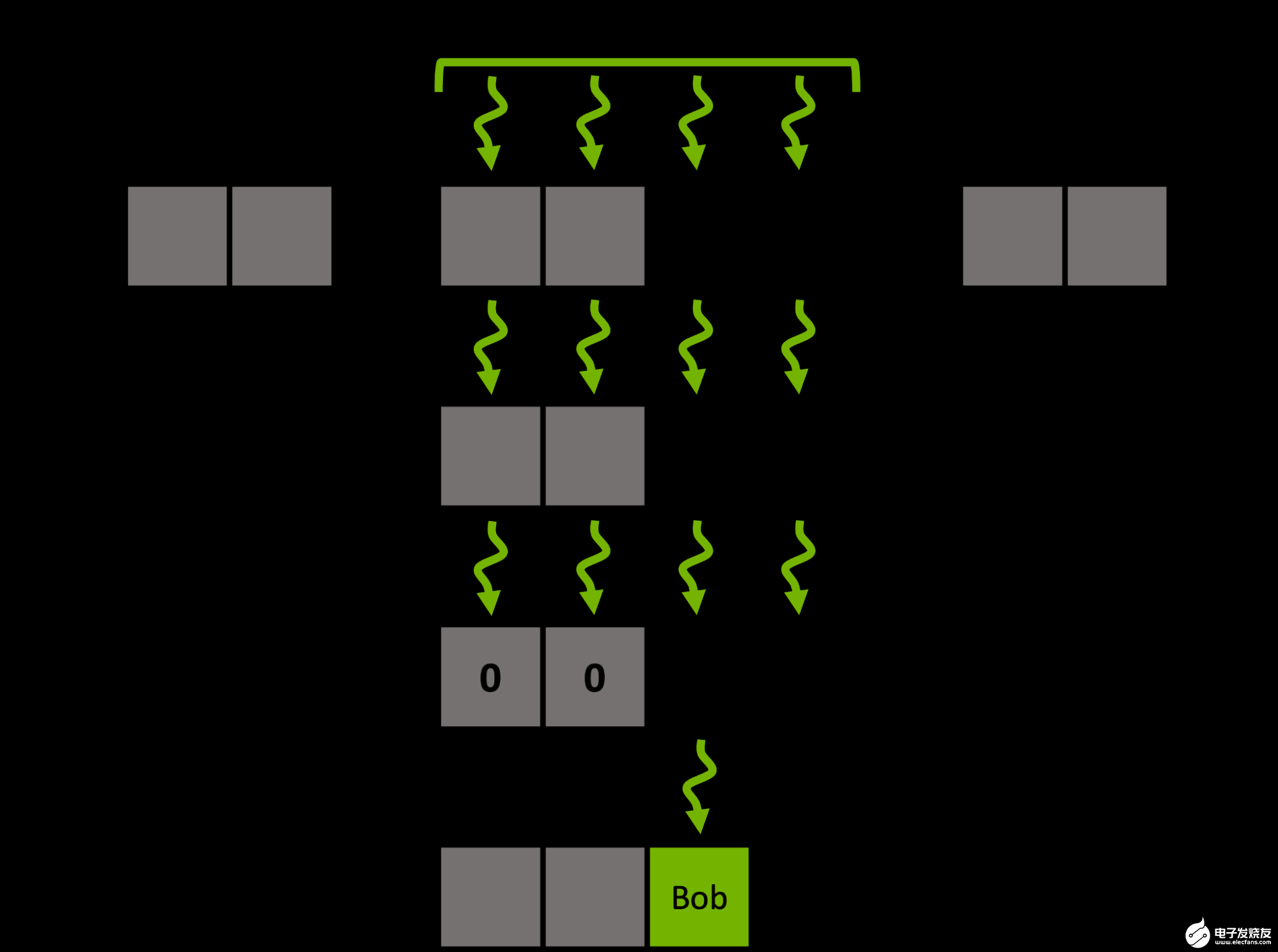图 3 。密钥 Bob 的组协作探测步骤及其中间步骤

下面的代码扩展了之前引入的 insert 函数，以使用扭曲中的四个连续线程协同插入一个键。cg::thread_block_tile<4>表示子 rp 中的四个线程。

 

enum class probing_state { SUCCESS, DUPLICATE, CONTINUE };


__device__ bool insert(cg::thread_block_tile<4> group, Key k, Value v) {
// get initial probing position from the hash value of the key
auto i = (hash(k) + group.thread_rank()) % capacity;
auto state = probing_state::CONTINUE;
while (true) {
  // load the contents of the bucket at the current probe position of each rank in a coalesced manner
  auto [old_k, old_v] = buckets[i].load(memory_order_relaxed);
  // input key is already present in the map
  if(group.any(old_k == k)) return false;
  // each rank checks if its current bucket is empty, i.e., a candidate bucket for insertion
  auto const empty_mask = group.ballot(old_k == empty_sentinel);
  // it there is an empty buckets in the group's current probing window
  if(empty_mask) {
    // elect a candidate rank (here: thread with lowest rank in mask)
    auto const candidate = __ffs(empty_mask) - 1;
    if(group.thread_rank() == candidate) {
      // attempt atomically swapping the input pair into the bucket
      bool const success = buckets[i].compare_exchange_strong(
                      {old_k, old_v}, {k, v}, memory_order_relaxed);
      if (success) {
        // insertion went successful
        state = probing_state::SUCCESS;
      } else if (old_k == k) {
        // else, re-check if a duplicate key has been inserted at the current probing position
        state = probing_state::DUPLICATE;
      }
    }
    // broadcast the insertion result from the candidate rank to all other ranks
    auto const candidate_state = group.shfl(state, candidate);
    if(candidate_state == probing_state::SUCCESS) return true;
    if(candidate_state == probing_state::DUPLICATE) return false;
  } else {
    // else, move to the next (linear) probing window
    i = (i + group.size()) % capacity;
  }
}
}

 

哈希表插入函数的前面的代码示例是 cuCollections cuco::static_map的实际实现的简化版本。

图 4 显示了在 NVIDIA A100 80 GB GPU 上测量的不同组大小和表占用率的非协作和协作探测方法的性能，没有具体化。

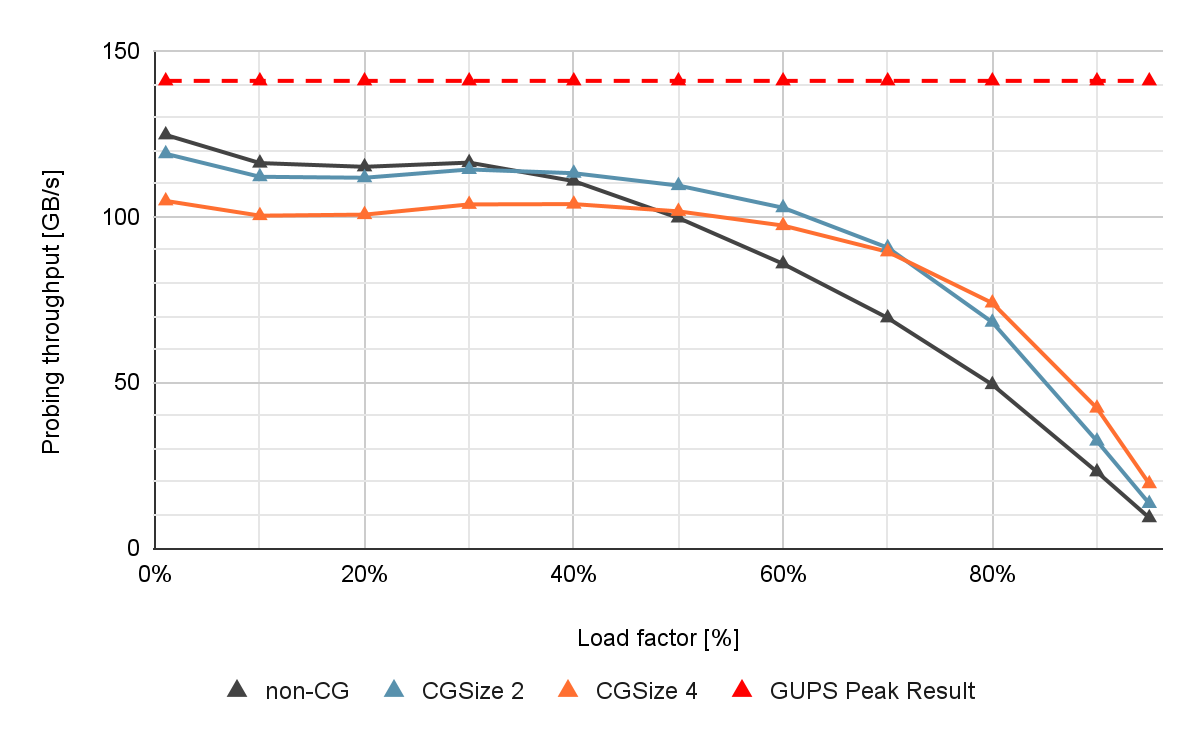图 4 。通过协作探测，吞吐量以 GB / s 为单位（越高越好）。红色虚线显示了峰值 GUPS 结果，它提供了在该系统上可以实现的吞吐量上限。

如果负载系数较低，则非合作（非 CG ）表现出接近最佳性能。然而，如果负载因子增加，则吞吐量会由于冲突次数增加和探测序列较长而急剧下降。这是有问题的，因为较高的表加载系数对应于更好的内存利用率。

协作探测提高了此类高负载因数场景的性能。与非合作方法相比，当负载系数较高时，如果组大小为 4 ，可以观察到插入吞吐量高出 13% ，查找吞吐量高出 40% 。

长探测序列也出现在具有高密钥乘数的多值场景中，因为相同的密钥遍历相同的桶序列。合作探测也有助于加快这些场景。

有关组协作哈希表探测的更多信息，请参见 Parallel Hashing on Multi-GPU Nodes 和 WarpCore: A Library for Fast Hash Tables on GPUs 。

现有 CPU 和 GPU 哈希图比较

多年来，已经提出了多种 C ++哈希图实现。其中最流行的是libstdc++/libc++ std::unordered_ map 和 Abseil absl::flat_hash_map。这些是顺序实现，从多个线程使用它们需要额外的同步。

TBB 中的tbb::concurrent_hash_map和 Folly 中的folly::AtomicHashMap是并发多线程 CPU 数据结构的示例。 GPU s 中可用的少数实现之一是 Kokkos 库中的kokkos::UnorderedMap。

将上面提供的映射实现的性能与 cuCollection cuco::static_map进行比较。基准设置如下。

首先，插入 227（ 1GB ）唯一的 4 字节密钥/ 4 字节值对，然后查询同一组密钥以检索它们的相关值。每次运行的目标工作台负载系数为 50% 。性能以内存吞吐量衡量（每秒 GB ；越高越好）。

结果如图 5 所示。cuco::static_map在单个 NVIDIA H100-80GB-SXM 上实现了 87.5 GB / s 的插入吞吐量和 134.6 GB / s 的查找吞吐量，这意味着与最快的 CPU 单线程和多线程实现相比，速度提高了超过数量级。此外， cuCollections 在本测试中的性能优于其他 GPU 实现kokkos::UnorderedMap，插入的性能为 3.8 倍，查找的性能为 2.6 倍。

请注意，在这个基准设置中，对于 CPU 侧的实现，每个操作的 I / O 向量都驻留在 CPU memory 中，而对于 GPU 侧的实施，则驻留在 GPU memory 中。如果数据向量需要驻留在 GPU 哈希映射的 CPU 存储器中，这将要求首先将输入数据移动到 GPU ，然后将结果移回 CPU 存储器。

这可以通过显式（异步批处理）复制或使用 CUDA 的 unified memory 概念自动页面迁移来实现。结果表明，我们实现的吞吐量始终远远高于 H100 上 PCIe Gen4 甚至 PCIe Gen5 的实际可用带宽。这意味着该方法能够使 CPU 和 GPU 之间的链路完全饱和。

换句话说，即使数据不在 GPU 内存中， cuCollections 也能以系统 PCIe 带宽的速度构建和查询哈希表。此外，由于 GPU 和 GPU 之间的快速 NVLink-C2C 互连， NVIDIA Grace Hopper Superchip 可以提供额外的加速，释放哈希表的全部吞吐量。相比之下， CPU 哈希映射通常实现比 PCIe 低得多的吞吐量。

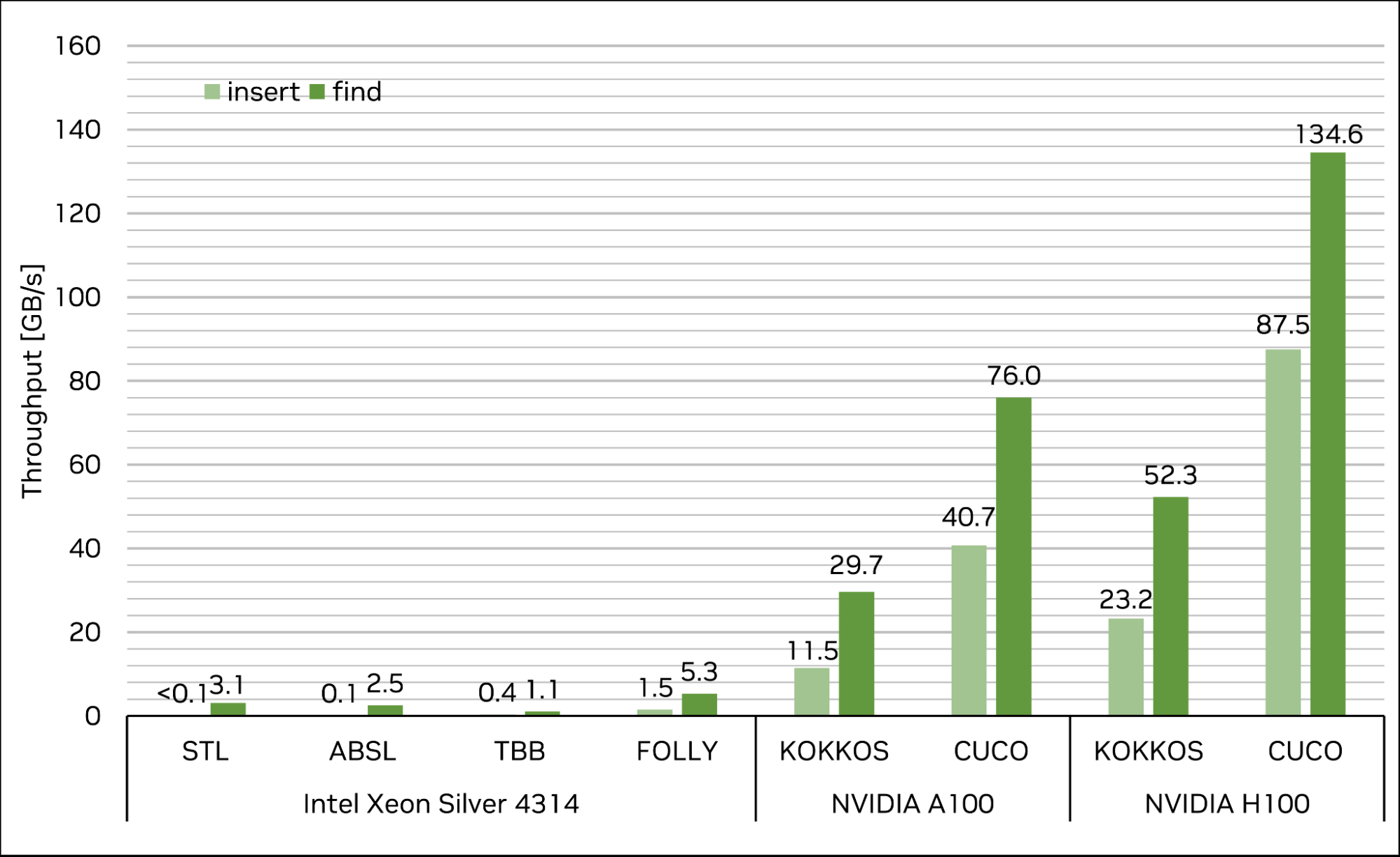图 5 。流行 CPU 和 GPU 哈希图实现的性能比较

多列关系联接示例

本节以 GPU 哈希表如何用于实现复杂算法的真实示例为特色。

cuDF 是用于数据分析的 GPU 加速库。它为数据操作（如加载、连接和聚合）提供原语。通过利用 cuCollections 哈希表，它使用哈希连接算法来执行连接操作。

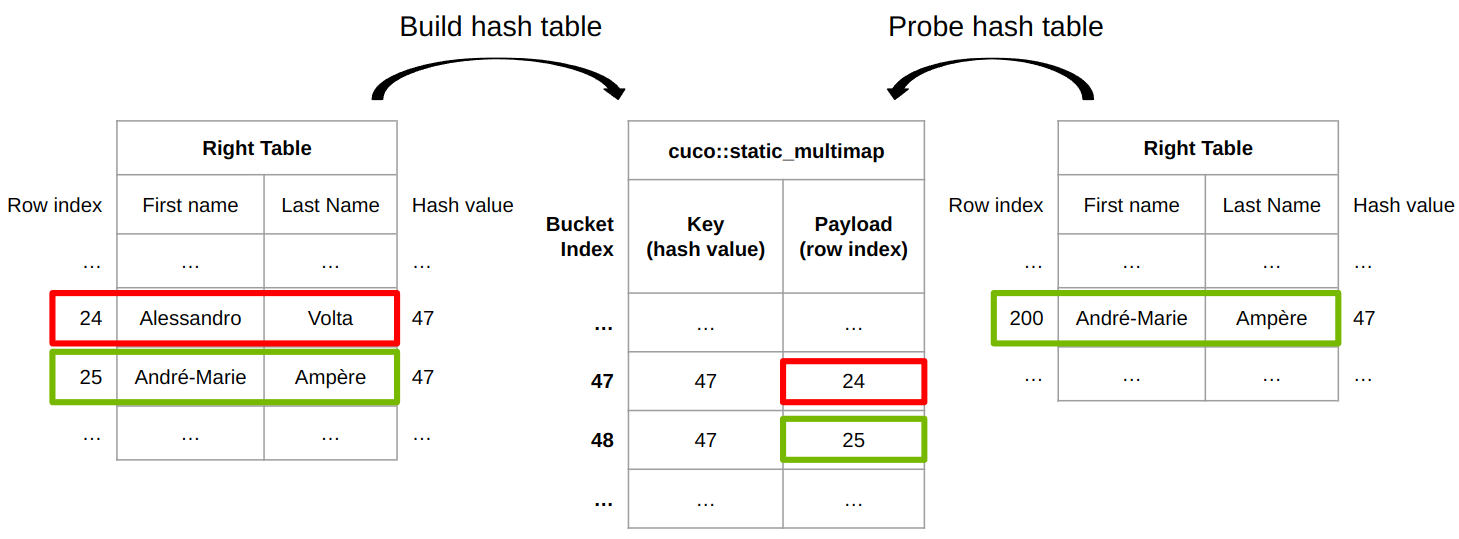图 6 。 RAPID cuDF 中内部连接实现的构建和探测阶段

图 6 显示了 cuDF 连接实现如何为内部连接工作。 cuDF 提供了一个内置的哈希函数，用于将任意类型的行哈希为哈希值。不同的行可以具有相同的哈希值，因此需要行相等性检查来确定两行是否真正相同。

左侧的表格用于填充 cuco::static_multimap 其中键是行的哈希值，有效载荷是关联的行索引。行 24 插在铲斗 47 上，行 25 插在铲斗 48 上。在探测阶段，右表中的行 200 的哈希值为 47 ，这与哈希表中的桶 47 的哈希值（或相同密钥）相同。

为了最终确定两行是否相等，将右侧表中的{ Andr é -Marie ， Amp è re }的行索引 200 与左侧表中的｛ Alessandro ， Volta ｝的行索引 24 传递给行相等函数 row_equal(200, 24) 。

最后，这两行并不相同，因此左侧表的第 24 行不匹配。最后，左表的第 25 行与右表的第 200 行匹配，因为哈希值相同，并且行相等性检查（ row_equal(200, 25) ）也通过。

基准连接操作是一个复杂的主题，因为有许多大小、选择性等选项。有关详细信息，请参见 How to Get the Most out of GPU Accelerated Database Operators 和 Effective, Scalable Multi-GPU Joins 。

如何在代码中使用 GPU 哈希图

GPU s 非常适合于哈希图等并发数据结构。这一切都是从高带宽存储器架构开始的，对于许多小的随机读取和原子更新，该架构比 CPU 快一个数量级。这直接转化为 GPU 上高效的哈希表插入和探测性能。

这篇文章介绍了设计大规模并行哈希图时的几个重要考虑事项： 1 ）具有开放寻址的哈希桶的平面内存布局，以解决冲突。作为 cuCollections 库的一部分，您可以在 GitHub 上找到快速灵活的哈希图实现。