深度分析振荡频率中的能量损失

　　我们知道，振荡频率有三个重要因素：时间周期、幅度和波长。时间周期表示振荡的一个完整周期之间的间隔，而幅度是振荡的最大值和最小值。下面我们看看振荡在波形中的样子。

　　

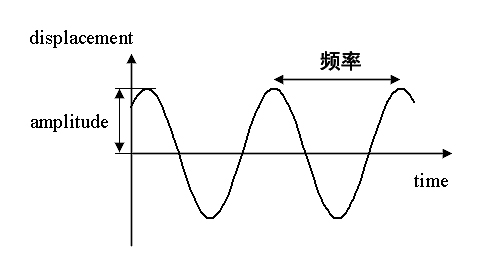
　　从时间周期来看，振荡波的频率可以通过以下公式计算：

　　频率（f）=1/时间段

　　用最短的物理距离来完成一个周期的振荡，该参数称为波长，它是连续间隔上同一点之间的物理测量。

　　一、电子产品中的振荡频率

　　在电子设计中，经常会发现振荡频率及其各自的电路。许多组件依赖于精确的振荡频率来发挥作用。而且电子设备中的振荡波形在时间周期和幅度上通常不均匀。

　　稳定且精确的振荡频率用于为设计中的实时时钟供电。时钟依赖于晶振，通常是32.768Khz晶振，以提供增加时钟寄存器所需的“滴答声”。单片机则依靠统一的振荡频率以所需的速度执行其代码。

　　振荡器电路也用于电视、收音机和其他类型的射频发射器。它们生成具有特定频率的载波信号，然后由信息调制。在接收端，谐振器被调谐到振荡频率以拾取和解调射频信号。

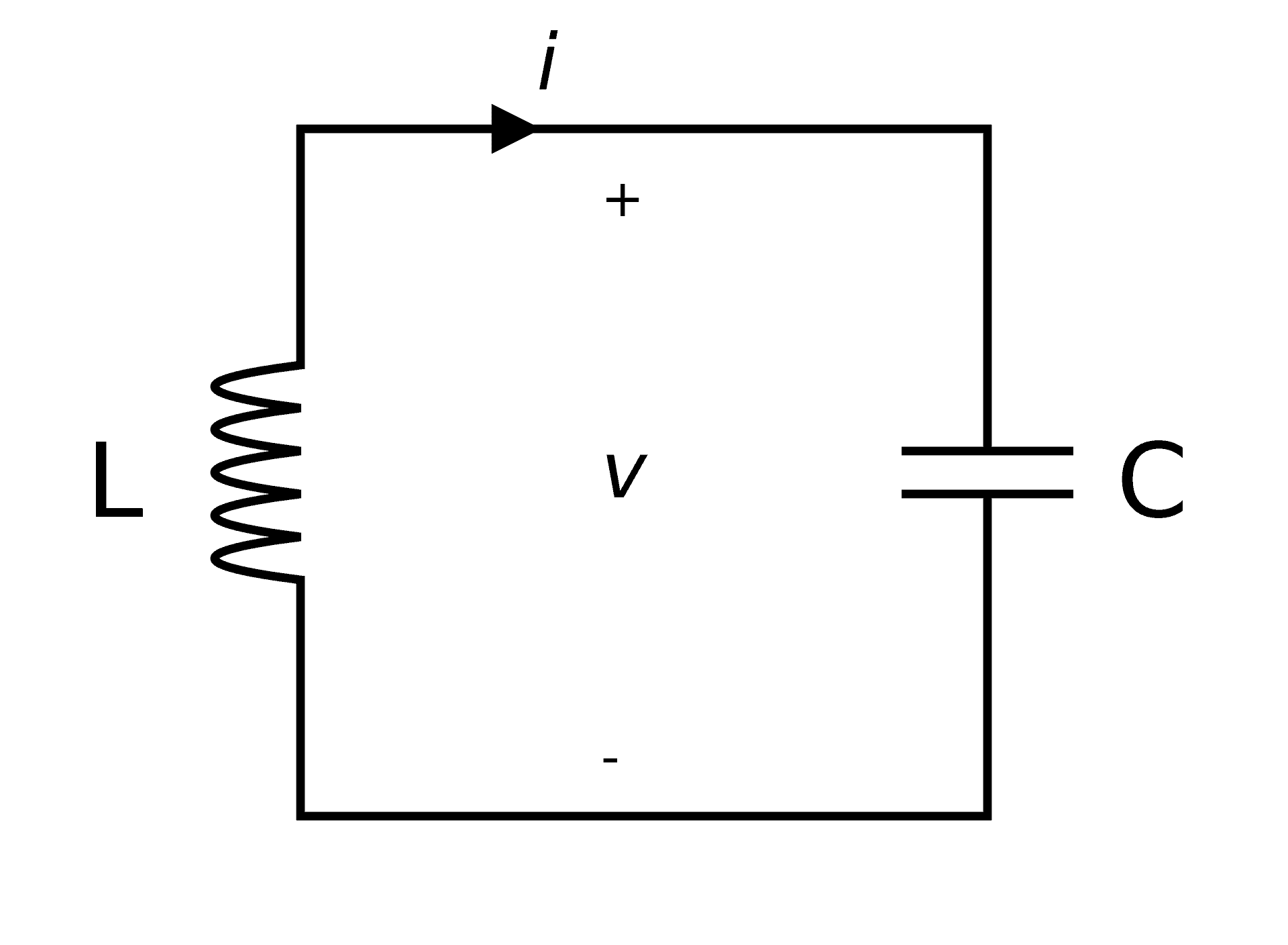
　　有几种类型的振荡器，但它们的核心是LC电路。它也被称为LC谐振电路。根据楞次定律，电流在充满电的电容器和电感器之间振荡。当电感器充电时，会产生一个与电流变化相反的反电动势，从而以相反的方向对电容器充电。下图为LC谐振电路，振荡电路的共同核心。

　　

　　二、振荡频率中的能量损失

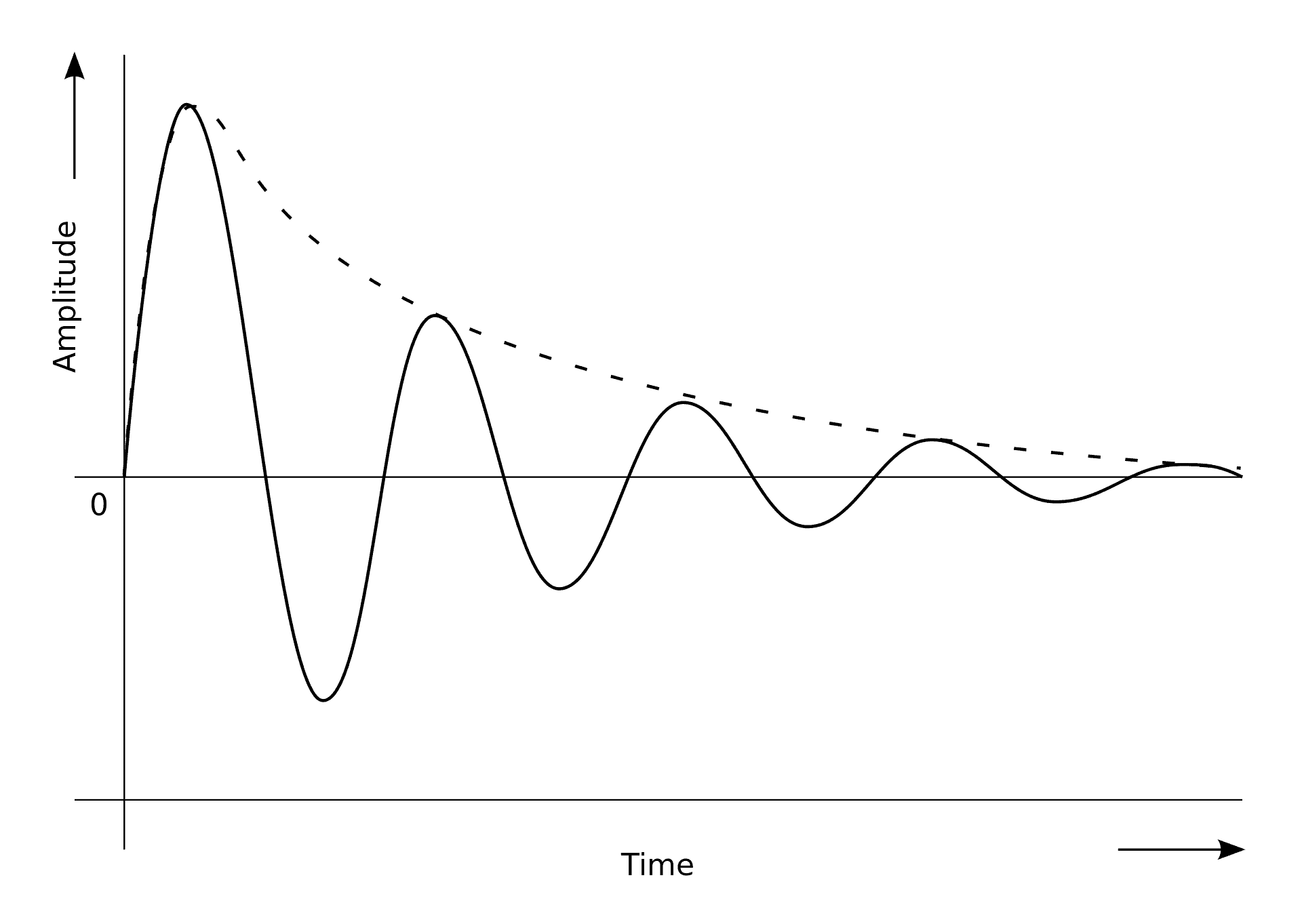
　　理想情况下，一旦周期开始，LC电路将产生具有相等幅度的连续振荡波形。然而，在真实世界的LC电路中不可能出现完美的正弦振荡波形。随着时间的推移，组件和连接的阻抗会导致能量损失。振幅逐渐减小的阻尼振荡，结果，将会出现阻尼振荡，其中幅度逐渐减小。LC电路要实现连续振荡，需要反馈信号。如下所示，反馈信号用于放大现有信号并补偿损失。

　　

　　振荡器电路的实际应用通常涉及调谐集电极振荡器、基于调谐的振荡器、哈特莱振荡器和考毕兹振荡器等变体。这些振荡器电路使用晶体管或运算放大器来放大振荡信号。

　　在设计自持振荡电路时，经常需要添加电阻进行调节（阻尼），重要的是要确保它既不是过阻尼也不是欠阻尼。这意味着确保闭环增益Aβ等于1。A是放大器电路的增益，而β等于反馈网络增益。