

带你认识带隙基准电路
电子说
描述
01
带隙基准理论基础
与温度关系很小的电压或者电流基准,在实际电路设计中具有重要的应用,比如在电流镜结构中,需要对一“理想的”基准电流进行精确复制,这一“理想的”基准电流,一般由带隙基准电路产生。怎样才能产生一个对温度变化保持恒定的量呢?我们可以这样假设:如果将两个具有相反温度系数的量,以适当的权重进行相加,那么最终的结果就会显示出零温度系数。例如,对于随温度变化向相反方向变化的电压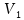 和
和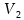 来说,我们选取系数
来说,我们选取系数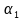 和
和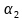 ,使得
,使得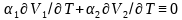 ,这样就得到了具有零温度系数的电压基准
,这样就得到了具有零温度系数的电压基准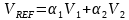 。下面,我们将分析,如何产生这两种随温度变化反方向变化的电压。
。下面,我们将分析,如何产生这两种随温度变化反方向变化的电压。
02
负温度系数电压
双极性晶体管的基极-发射极电压,具有负温度系数。对于一个双极性器件,我们可以写出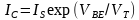 ,其中,
,其中,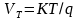 ,饱和电流
,饱和电流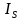 正比于
正比于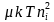 ,其中
,其中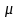 为少数载流子浓度,
为少数载流子浓度,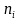 为硅的本征载流子浓度。这些参数与温度的关系可以表示为
为硅的本征载流子浓度。这些参数与温度的关系可以表示为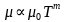 ,其中,
,其中,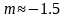 ,并且
,并且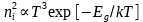 ,其中,
,其中,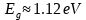 ,为硅的带隙能量,所以有:
,为硅的带隙能量,所以有:

其中,b为一比例系数。写出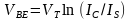 ,我们就可以计算基极-发射极电压随温度的系数了。在
,我们就可以计算基极-发射极电压随温度的系数了。在 对T取导数时,我们一定要知道
对T取导数时,我们一定要知道 也是温度的系数。为了简化分析,我们暂时假设
也是温度的系数。为了简化分析,我们暂时假设 保持不变,这样有:
保持不变,这样有:

于是我们有:

所以有:

最终可得到:

上式给出了在给定温度T下基极-发射极电压的温度系数,从中可以看出,它与 本身的大小有关。当
本身的大小有关。当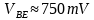 ,T=300K时,
,T=300K时, 。
。
03
正温度系数电压
如果两个双极性晶体管工作在不相等的电流密度下,那么它们的基极-发射极电压的差值就与绝对温度成正比。
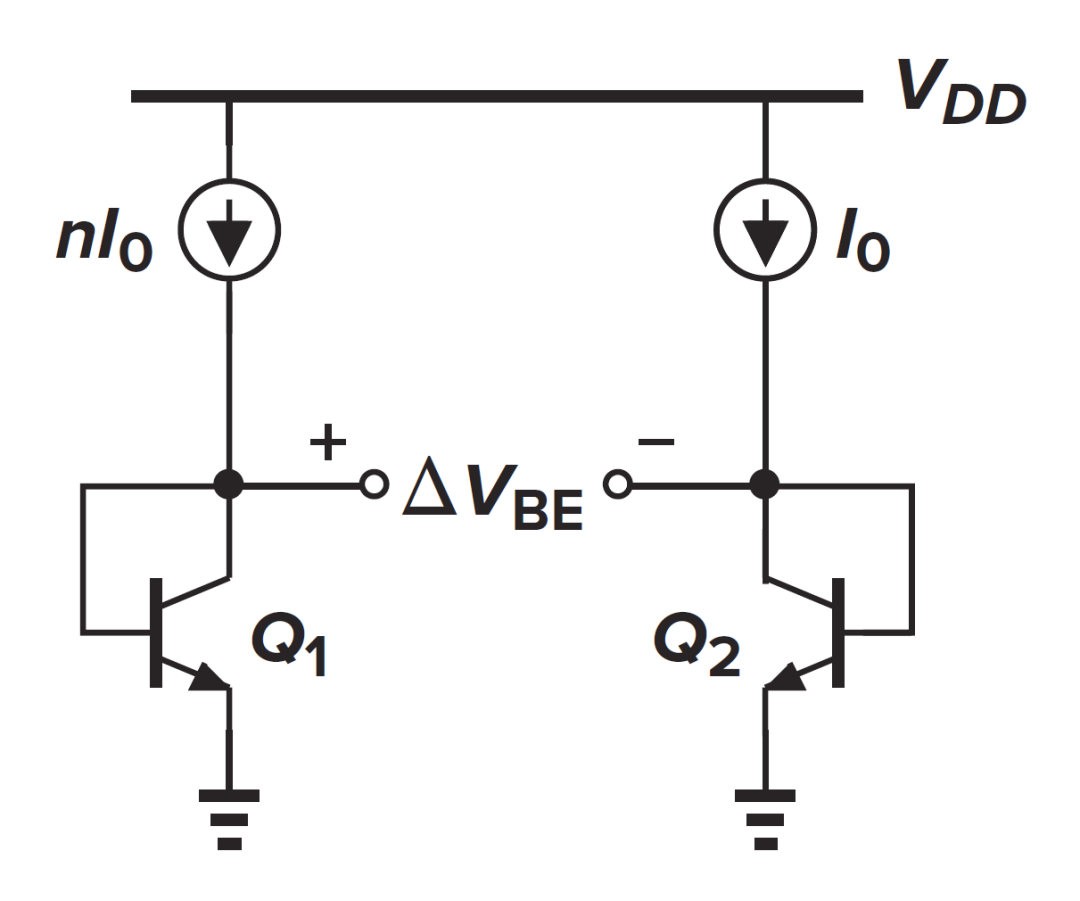
图一
对于图一,如果两个同样的晶体管( )偏置的集电极电流分别为
)偏置的集电极电流分别为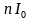 和
和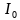 并忽略它们的基极电流,那么有:
并忽略它们的基极电流,那么有:
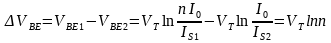
这样, 的差值就表现出正温度系数:
的差值就表现出正温度系数:

04
带隙基准
利用上面得到的正、负温度系数的电压,我们现在可以设计出一个令人满意的零温度系数的基准。我们有 ,这里
,这里 是两个工作在不同电流密度下的双极性晶体管的基极-发射极电压的差值。那么我们怎么选择系数
是两个工作在不同电流密度下的双极性晶体管的基极-发射极电压的差值。那么我们怎么选择系数 和
和 呢?在室温下,
呢?在室温下, ,
, ,因此我们可以选择令
,因此我们可以选择令 ,选择
,选择 使得
使得 ,也就是
,也就是 ,这样得到的零温度系数的基准为:
,这样得到的零温度系数的基准为:
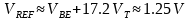
05
实现电路

图二
图二为带隙基准电路的实现原理图,Q1为单个晶体管,Q2为n个并联的晶体管,我们在X点和Y点引入运算放大器,利用运算放大器的特性强制X点和Y点点位相等,那么有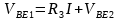 ,即
,即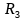 I=
I= ,所以有
,所以有 。选择
。选择 ,我们有输出电压为:
,我们有输出电压为:

我们选择合适的电阻值,即可满足 的条件。例如,可以选择n=31,
的条件。例如,可以选择n=31, 。
。
06
总结
至此,我们已经完成了最简单的带隙基准电路的设计。在实际电路中,由于运放的输入失调等效应,还需要加入反馈回路等结构,以确保带隙基准电路能够稳定的工作。最终实现的电路会相对复杂,但是核心电路的原理基本上大同小异。
-
带隙基准电路设计原理2023-07-06 3472
-
带隙基准是什么?带隙基准的结构是由哪些部分组成的?2021-06-22 2034
-
带隙基准是什么_带隙基准电路的优点2019-08-06 9459
-
一种高精度BiCMOS电流模带隙基准电路设计2019-07-12 2932
-
基于LDO稳压器的带隙基准电压源设计2018-10-09 3111
-
带隙基准电路_cmos无运放带隙基准源2018-01-11 18321
-
cmos带隙基准电压源设计2017-11-24 24779
-
带隙基准电压源及过温保护电路2017-09-07 1332
-
带隙电压基准源的设计与分析2012-05-24 1800
-
基于汽车环境的带隙基准电压源的设计2010-12-22 792
-
新型BiCMOS带隙基准电路的设计2010-11-02 2700
-
带隙基准源的现状及其发展趋势2010-07-29 845
-
低温漂低功耗的带隙基准源技术设计2010-04-28 2189
-
带隙基准电路的研究2009-03-11 1592
全部0条评论

快来发表一下你的评论吧 !

