

研究VCO相位噪声的新视角—广义阿德勒方程
电子说
描述
相位噪声是VCO的核心指标,衡量了输出信号频谱的纯净程度。研究相位噪声的来源和形成机制,对VCO设计与优化有着重要的意义。当前学术界有若干种相位噪声分析模型并存,如Leeson的线性时不变模型,Hajimiri的ISF模型等等,他们的切入角度和侧重点各有不同,实际使用中也存在着各自的局限。本文简要介绍一种新的相位噪声分析方法,区别于常见的理论模型,该方法提供了一种分析VCO相位噪声的新视角。
01
振荡过程中的牵引现象
相位噪声的形成机制非常复杂,但是总体上都可以概括为振荡过程被牵引的产物。LC振荡电路进入稳态振荡过程之后,是一个典型的非线性时变系统,此时电路中的噪声、干扰以及某些非线性参数都会对输出信号产生影响,造成信号相位的随机微小扰动,相位噪声也就由此产生,振荡器中噪声转化为相位噪声的过程称为上变频(up-conversion)。
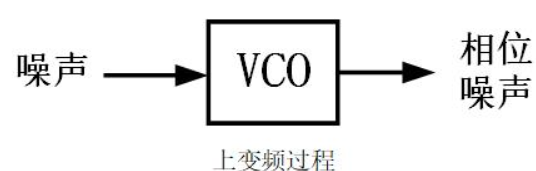
不同理论模型对上变频的描述也各有不同,例如大名鼎鼎的Hajimiri模型就是将脉冲灵敏度函数(ISF)作为桥梁,从时域角度阐述了这一过程。

如上图,噪声电流经过时变系统(ISF)转化为信号的额外相移,再经过相位调制形成信号频率附近的边带,即相位噪声。具体的推导过程本文不再赘述,可以参看文献 ^[1]^ 。
02
弱注入对振荡信号的影响
与Hajimiri模型不同,广义阿德勒方程(generalized Alders equation)则是从频域出发对上变频过程进行分析。考虑一个理想的振荡电路,受到一正弦注入电流的影响,假设注入电流的幅度和相位分别为in和θ n ,如下图

广义阿德勒方程给出了振荡信号与注入电流之间的关系 ^[2]^ :

其中 是振荡频率,
是振荡频率, 是振荡电压信号的瞬时相位,
是振荡电压信号的瞬时相位, 是自由振荡电流,Q是谐振器的品质因数。由此可见,信号的相位变化主要与品质因数,注入电流与自由振荡电流的比值有关。解这一微分方程即可得出特定强度的注入电流造成的相位变化。
是自由振荡电流,Q是谐振器的品质因数。由此可见,信号的相位变化主要与品质因数,注入电流与自由振荡电流的比值有关。解这一微分方程即可得出特定强度的注入电流造成的相位变化。
03
具体电路分析
根据上文的结论,要确定振荡信号的相位变化,需要得到工作频率,品质因数,自由振荡电流和注入电流强度等参数。这些参数在确定了具体电路形式之后都能方便地取得,以常见的交叉耦合振荡器为例:

如果偏置电流为I,根据电路性质,自由振荡电流的强度 应为4I/π,注入电流
应为4I/π,注入电流 为LC损耗电阻产生的热噪声。等效电路为:
为LC损耗电阻产生的热噪声。等效电路为:

考虑振荡频率附近频偏为 的噪声电流,应用广义阿德勒方程,可知:
的噪声电流,应用广义阿德勒方程,可知:

如果忽略噪声的相位,那么振荡信号的额外相位满足以下微分方程:

解之,得

功率谱密度为

根据相位噪声的定义不难得出:

该相位噪声的形式与Leeson方程的结论完全一致 ^[3]^ ,证明了广义阿德勒方程研究相位噪声的可行性。
04
小结
广义阿德勒方程的优点主要体现在两方面,第一,它从单频点的注入电流入手分析相位噪声,这一切入点的优势在于,不需要针对不同性质的噪声单独建立模型。众所周知,振荡电路中存在着各种各样的噪声,频率特性也各不相同。

上图给出了VCO相位噪声谱的一般规律,研究结果表明,第一区的相位噪声主要由管子闪烁噪声产生,第二区则由沟道噪声及热噪声转化而来。此外,非线性电容、AM-PM转换等现象也会增加相位噪声。传统理论模型中需要对以上所有的相位噪声来源分别进行分析,计算量较高。而广义阿德勒方程则能够将噪声拆解成无穷多个微小注入电流的组合统一计算,增强了适用性。
第二,广义阿德勒方程基于注入电流分析VCO的噪声行为,这种思路能够方便地推广到QVCO的场合。文献 ^[4]^ 使用该方法,对QVCO的相位噪声、相位误差、工作模式以及幅度稳定性进行了系统的理论分析,为电路设计指明了方向。
-
直播预告 | 干簧技术应用:汽车行业新视角2024-11-13 2600
-
ADI推出全新四频段VCO 提供更低相位噪声及低水平电流消耗2020-12-05 1873
-
Z-COMM VCO的相位噪声测量2009-06-13 3533
-
关于ADF4351开环VCO相位噪声测试问题2018-08-02 4148
-
如何根据基本的数据表规格估算出P L L的相位噪声2018-08-31 2184
-
用于微波无线电的高性能SiGe PLL与低相位噪声GaAs VCO配对2019-09-26 1672
-
如何用交叉耦合电流饥饿型VCO设计实现降低时钟频率的相位噪声?2021-02-25 3649
-
电源噪声是怎么对VCO造成影响的?是由于电容的耦合吗?2021-06-24 1991
-
有谁能解答关于仿真VCO相位噪声的问题吗?2021-06-25 2412
-
RF MEMS压控振荡器及相位噪声特性的研究2010-02-26 923
-
高速低相位噪声VCO设计2009-05-09 3060
-
怎样优化PLL环路来达到理想的相位噪声和抖动2019-04-10 7656
-
宽带VCO在坚固耐用的RoHS兼容模块中结合了低相位噪声和高输出功率2021-04-18 682
-
罗德与施瓦茨大幅提高相位噪声分析和VCO测量组合产品的性能2023-02-12 1872
-
为MAX2309优化VCO相位噪声2023-06-08 1972
全部0条评论

快来发表一下你的评论吧 !

