

二端口网络噪声分析方法在低噪声放大器中的应用
电子说
描述
系统中的噪声限制了一个电路能够正确处理的最小信号电平,它与功耗、速度、线性度之间是相互制约的。比如在一个接收机中,系统整体的噪声系数和系统带宽和载噪比共同决定该接收机的灵敏度,越低的噪声系数意味着接收机能检测并接收到更低的信号功率,其灵敏度越高。这说明了在电路中进行噪声优化和分析的必要性。此篇通过分析电阻和MOS管器件噪声的来源,主要介绍二端口网络噪声分析方法,并在设计低噪声放大器时应用该方法对器件合理选型以在输入匹配的前提下实现尽可能低的噪声系数。
01
基本噪声源
由于噪声是一个随机变量,直接从时域研究幅值较为困难,因此可以根据噪声的统计特性,可以将噪声利用功率密度谱的方式定义成S(f),其单位为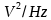 ,其在电路模型中又通常可以表示为电压噪声源或电流噪声源的形式,这些噪声电流源(或噪声电压源)既可能是相关的,也可能是无关的,这主要取决于在器件中噪声源的相关性。
,其在电路模型中又通常可以表示为电压噪声源或电流噪声源的形式,这些噪声电流源(或噪声电压源)既可能是相关的,也可能是无关的,这主要取决于在器件中噪声源的相关性。
噪声通过大类大致可分为热噪声、散粒噪声、闪烁噪声、爆米噪声等。对于散粒噪声,在MOSFET中几乎不是一个显著的噪声;对于神秘的MOS管闪烁噪声,其公式包含着各种经验参数,比较统一的结论是电荷的捕获现象能够解释1/f噪声的产生、增大晶体管可以减少1/f噪声等,在混频器和VCO中也存在对闪烁噪声的分析;对于爆米噪声,用数学描述它的意义不大,因为它时时在发生变化,同样人们对其认知也有限。一般,由于希望通过建模的方式去分析噪声,因此我们侧重于分析热噪声(由于其比较成熟的理论公式和来源分析)。
电阻热噪声公式:
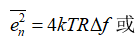
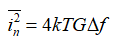
MOS管沟道和栅热噪声公式:
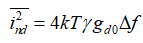
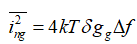
上述公式的推导和现代理论对于上述公式的修正和考虑可以参见参考文献。
02
二端口网络的噪声因子
网络噪声性能的优劣主要通过噪声因子来衡量,可以定义为:

进一步,为适用不同二端口网络的分析,网络的噪声特性可以用输入参考噪声电压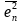 和电流
和电流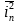 表示,则噪声系数
表示,则噪声系数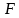 的表达式为:
的表达式为:
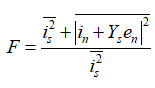
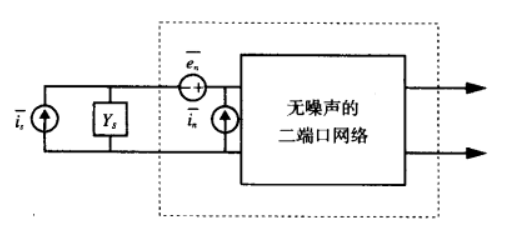
这里的二端口网络由一个导纳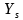 以及等效的并联噪声电流
以及等效的并联噪声电流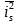 构成的噪声源驱动。
构成的噪声源驱动。
由于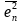 和
和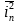 可能表现出相关性,将
可能表现出相关性,将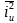 表示与
表示与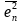 无关的部分,其噪声功率可以直接相加;相关部分
无关的部分,其噪声功率可以直接相加;相关部分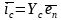 ,将因此可以将噪声系数表达式简化为,:
,将因此可以将噪声系数表达式简化为,:
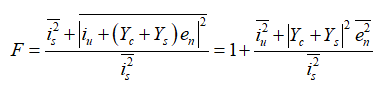
观察上式,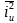 、
、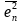 、
、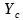 是网络特有的参数,
是网络特有的参数,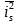 和
和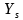 是噪声驱动源的参数,每个噪声源都可以看作一个等效电阻或电导产生的热噪声,电纳部分不产生噪声:
是噪声驱动源的参数,每个噪声源都可以看作一个等效电阻或电导产生的热噪声,电纳部分不产生噪声:
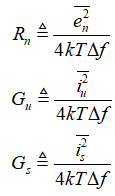
则噪声因子最后可以只用阻抗和导纳项表示:
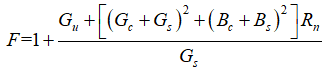
观察上式,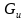 、
、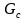 、
、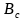 、
、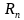 是网络特有的参数,
是网络特有的参数,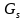 、
、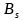 是驱动源电导和电纳。在设计中,若网络参数固定后(如表现为输入阻抗为50欧的限制),则可以求解平方项归零和对源电导求导,让噪声系数达到最小时的噪声源导纳如下:
是驱动源电导和电纳。在设计中,若网络参数固定后(如表现为输入阻抗为50欧的限制),则可以求解平方项归零和对源电导求导,让噪声系数达到最小时的噪声源导纳如下:
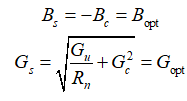
噪声因子可以表示成:
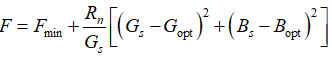
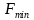 是最小噪声系数,常数噪声因子的等值线理论上是一些不相重叠的圆,称为恒噪声系数圆。
是最小噪声系数,常数噪声因子的等值线理论上是一些不相重叠的圆,称为恒噪声系数圆。
03
MOS管的端口网络噪声参数
在具体的网络分析中,掌握模型内部的噪声源在输入的表示还是必要的,这有助于推算每个网络特性参数,最后代入通式求解。对于单个MOS,若要进行噪声匹配,可以计算出输入网络噪声参数:
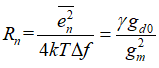
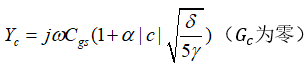
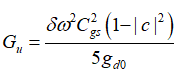
可以知道最优信号源电导值为:
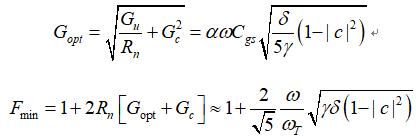
又由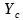 可知所要求的信号源电纳本质上是电感性的,且频率特性不正确(本应与
可知所要求的信号源电纳本质上是电感性的,且频率特性不正确(本应与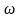 成反比),因此很难做到宽带噪声匹配,且计算过程与最大功率传输条件(阻抗匹配)无关。不过可以从
成反比),因此很难做到宽带噪声匹配,且计算过程与最大功率传输条件(阻抗匹配)无关。不过可以从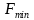 的表达式中得出两个有效的结论,即随着MOSFET尺寸的减小,截止频率提高,在噪声参数
的表达式中得出两个有效的结论,即随着MOSFET尺寸的减小,截止频率提高,在噪声参数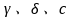 不变的前提下,最小噪声因子会降低;另外在后续放大器拓扑的噪声匹配中,将以
不变的前提下,最小噪声因子会降低;另外在后续放大器拓扑的噪声匹配中,将以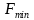 为参考,表示放大器拓扑能达到的的最小噪声因子。
为参考,表示放大器拓扑能达到的的最小噪声因子。
设计中通常要求网络对外展现一定的输入阻抗(如50欧),问题转变为在固定输入阻抗下的最优噪声系数求解。
04
源退化匹配下的噪声优化
为了获得50欧的输入阻抗,除了利用电阻强制匹配,负反馈电阻匹配,共栅电路匹配(沟道电阻)之外(这三种的信号通路都存在有噪声的电阻),一种比较巧妙的办法能够在不加入真实电阻的情况下获得输入阻抗的电阻分量,从而不降低放大器的噪声性能,即源退化电感结构。
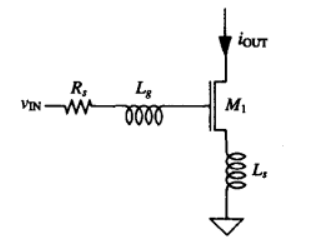
对于单管的输入阻抗大家都比较熟悉,但对于源退化单管,由于器件尺寸的缩小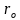 将呈现为一个有限值,这会导致共源负载谐振网络对输入阻抗较大的影响,尤其是在中心谐振频率附近输入阻抗下降严重:
将呈现为一个有限值,这会导致共源负载谐振网络对输入阻抗较大的影响,尤其是在中心谐振频率附近输入阻抗下降严重:
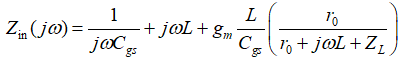
同时随着频率的上升,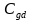 也将参与到输入阻抗实部的贡献:
也将参与到输入阻抗实部的贡献:
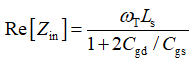
这直接要求我们利用Cascode结构和增加源退化电感值来减小输入阻抗的波动。
同样对于这种方式,依然可以求解输入网络噪声参数(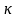 是栅极非准静态阻抗系数,一般为5):
是栅极非准静态阻抗系数,一般为5):
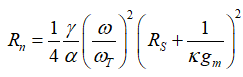
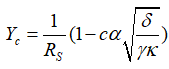
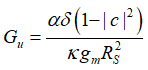
可求出对应的噪声因子:
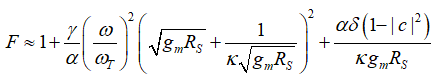
在上式中若保持过驱动电压固定的情况下,意味着截止频率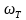 不变,从数学上讲存在最优跨导
不变,从数学上讲存在最优跨导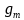 ,对应于最优的MOS宽度选型(注意不一定是功耗最优处)。
,对应于最优的MOS宽度选型(注意不一定是功耗最优处)。
对上式的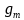 项求导并令其结果为零,在满足工作频率远小于特征频率和另外一个参数条件时,该结构能达到的最低噪声因子理论上就是单MOS管的最小噪声因子(代入
项求导并令其结果为零,在满足工作频率远小于特征频率和另外一个参数条件时,该结构能达到的最低噪声因子理论上就是单MOS管的最小噪声因子(代入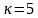 可见与式单管一致):
可见与式单管一致):
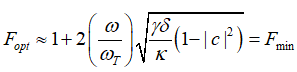
此时最优跨导为:
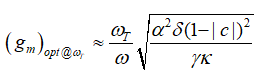
由于截止频率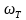 与跨导
与跨导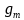 存在如下关系:
存在如下关系:
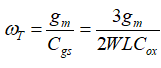
则MOS管的最优宽度W为:
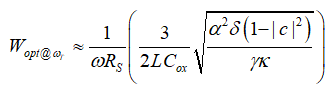
*注:在文献[2]中,最后也能得到与上述同样的结论,为直接使用了晶体管最优导纳公式,而上面为考虑非准静态阻抗得出的结论,两者复杂度完全不在一个层面。这里为谨慎起见,按照新的网络输入噪声参数计算。
因此在设计中,可以直接通过上述公式选择最优栅宽,这是一个与过驱动电压无关的量。假设工作在10.525GHz的中心频率处,我们选取: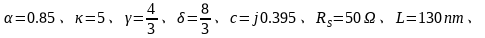
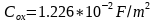 (由介电常数和厚度比值计算得到)
(由介电常数和厚度比值计算得到)
计算可得最优的栅宽约为140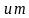 ,结合晶体管单元优化宽度为5
,结合晶体管单元优化宽度为5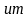 ,一般就可以合理选取晶体管的unit cell数目了,最优噪声因子约为1.19,噪声系数约为0.75dB。过驱动电压的选取可以根据噪声系数的要求选取最低的值。
,一般就可以合理选取晶体管的unit cell数目了,最优噪声因子约为1.19,噪声系数约为0.75dB。过驱动电压的选取可以根据噪声系数的要求选取最低的值。
另外,从公式中可以看出最小噪声因子和过驱动电压(即截止频率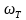 )成反比,更大的过驱动电压能导致更低的噪声系数,在其他条件不变的情况下放大器的功耗也会进一步增加。定性来讲,可以通过增加过驱动电压,改变栅宽 W (由于前面推得最优噪声因子的条件是在过驱动电压恒定下的噪声因子),使噪声因子不变的同时降低功耗。定量来说,需要构建直流功耗和噪声系数之间的数学关系,期间需要通过复杂的数学运算,在功耗确定的情况下,调整可变参数达到最优值,对应最小噪声因子。
)成反比,更大的过驱动电压能导致更低的噪声系数,在其他条件不变的情况下放大器的功耗也会进一步增加。定性来讲,可以通过增加过驱动电压,改变栅宽 W (由于前面推得最优噪声因子的条件是在过驱动电压恒定下的噪声因子),使噪声因子不变的同时降低功耗。定量来说,需要构建直流功耗和噪声系数之间的数学关系,期间需要通过复杂的数学运算,在功耗确定的情况下,调整可变参数达到最优值,对应最小噪声因子。
-
低噪声放大器放在哪里?低噪声放大器的作用是什么?2023-09-05 2599
-
低噪声放大器的设计原则2023-07-25 2789
-
低噪声放大器简介2023-01-07 2769
-
低噪声放大器设计资料2022-11-22 1296
-
S波段宽带低噪声放大器的设计与实现2022-07-08 1100
-
低噪声放大器介绍2021-07-27 3543
-
请问怎样可以提高低噪声放大器的测量精度?2021-04-14 2096
-
怎么设计低噪声放大器?2019-08-22 3769
-
低噪声放大器在射频测试测量中的应用2017-11-08 2548
-
低噪声放大器,低噪声放大器型号参数2017-09-11 6140
-
X波段低噪声放大器设计分析2011-08-02 3823
-
低噪声放大器的设计与仿真2010-07-21 706
-
宽带低噪声放大器噪声分析2010-05-13 3177
-
低噪声放大器,低噪声放大器是什么意思2010-03-05 4033
全部0条评论

快来发表一下你的评论吧 !

