

数字单周期控制的两相交错的CCM电路与PFC电路
电子说
描述
PFC 电路目的是要使电感电流Ig 的低频波形(50Hz)跟随整流后的输入电压波形Vg,同时又要保持输出电压为Vo。若控制电路的控制策略满足了电感电流与输入电压成比例且相位一致,整个变换器可以等效为一个电阻Re:
Vg = Re *Ig
对于BOOST变换器,输入电压和输出电压的关系满足:
Vg = Vo * (1 - d)
将上式合并得到:
Re * Ig = Vo * (1 - d)
定义Rs为PFC变换器中的电流检测电阻,将上式同时乘以Rs,可得:
Rs * Ig = Vo * Rs * (1 - d) / Re
若令:
Vm = Vo * Rs / Re
化简并整理:
Vm - Ig * Rs = Vm * d
上式即为单周期控制 PFC电路最重要的数学模型。Vm 在理论上是与Vo成比例的直流电压,若占空比d可以满足上式,则可以保证电感电流Ig 与半波正弦输入电压Vg 波形一致,从而实现PFC 功能。设变换器的开关周期为 T,构造单周期控制方程组:
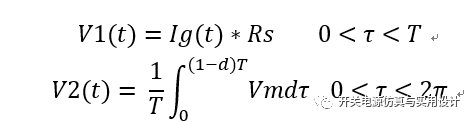
如果通过控制系统检测或计算到V1(t)或V2(t),并将其进行比较就可以得到开关器件的占空比d,实现单周期PFC控制。传统模拟单周期控制方案的核心是可复位的高速积分器和加法器,这两个功能利用硬件能比较容易的实现。

但是转到DSP里面做数字控制则会显得比较麻烦,首先是实现对采样电流的实时减法操作。然后根据减法器的输出去控制占空比,显然ADC的速度达不到这么高的速度。因此数字单周期控制必须根据模拟单周期控制的思想,做出一定的改进。在数字控制系统中,对输入电流采样的频率一般远高于120Hz。通常会采用单周期单次采样的方法,意思是在一个开关周期中只进行一次采样。一般情况下系统的采样频率与开关频率一致,故可以认为在一个开关周期内数字控制系统所采样到的Ig和调节信号Vm为固定值。
如果直接把单周期控制方程离散后,计算V2(t)会很复杂,也会浪费很多计算量。根据前文可知,在一个开关周期内数字控制系统所采样到的Ig和调节信号Vm为固定值,所以将单周期控制方程同时除以Vm用于简化V2(t)的计算,变为:
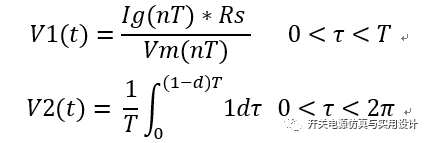
改进后的数字单周期控制方程将变得容易计算,通过对V1(t)和V2(t)进行比较实现功率级的开关控制,很容易得到控制所需的占空比。到此,所有理论已经建立,可以建立数字单周期的控制模型。电压环采样离散PID控制,在控制函数内部,将电感电流采样值除以电压环PID的输出值,即可得到在一个工频周期内的占空比控制值,通过与外部三角波进行比较,即可得到控制功率级的占空比,可见下图所示。
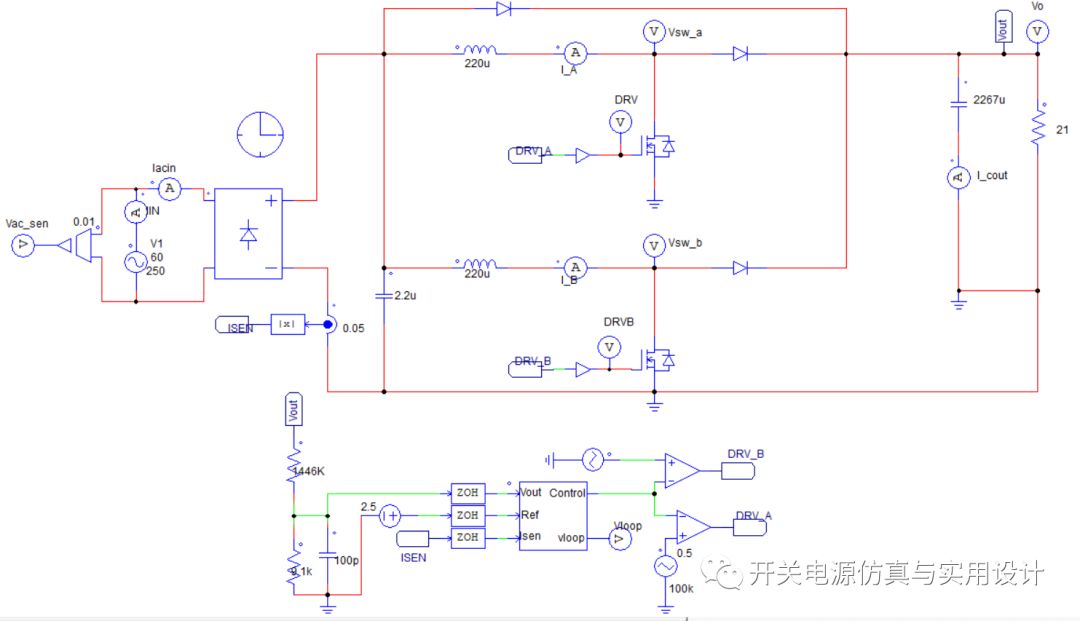
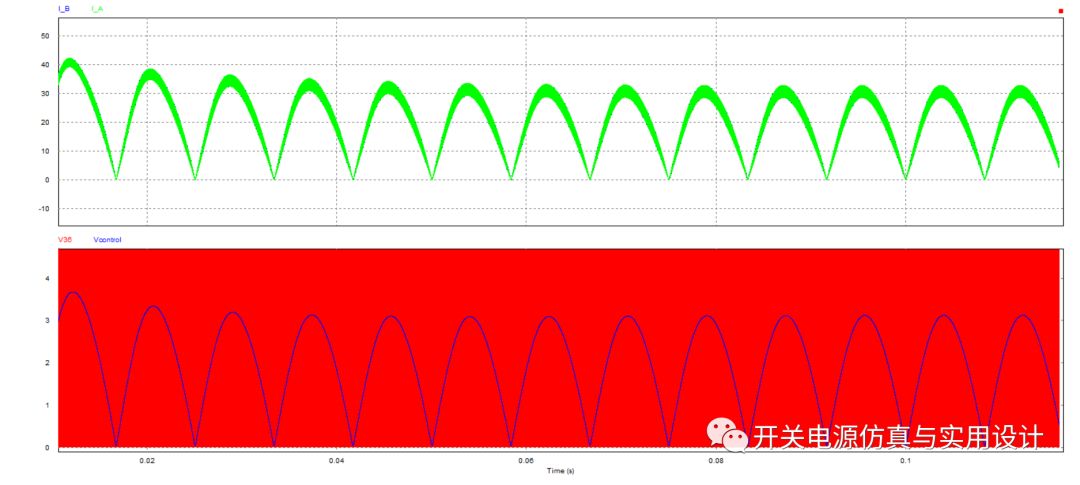
外部使用了两个错相180°三角波,频率为100KHZ,上升沿和下降沿各50%。将占空比控制值与三角波比较,就能得到控制功率级所需的占空比。可见从0 ~ 150ms的时域波形仿,最上面I_A和I_B为两个电感电流,Iacin为交流电源输入电流,Vo为直流输出电压。
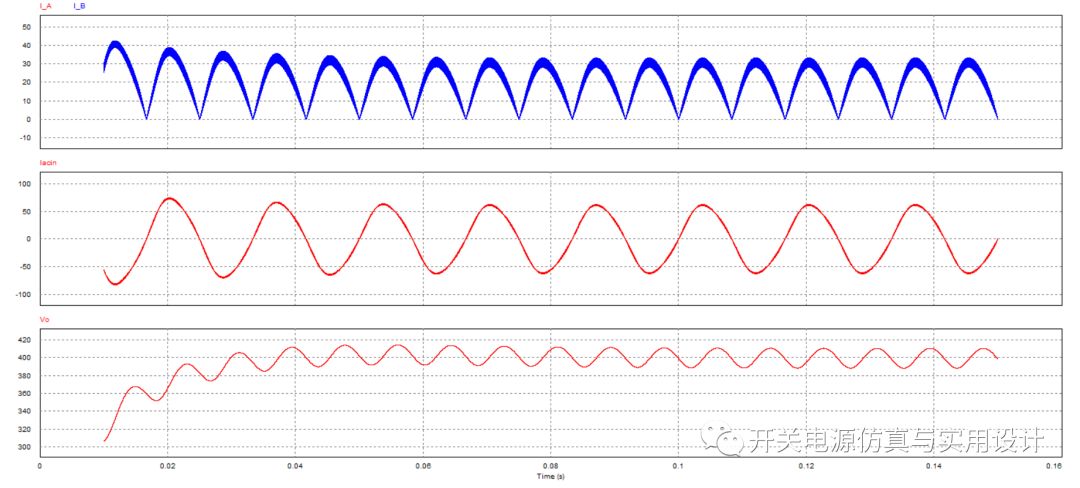
占空比控制值为下图中蓝色Vcontrol,红色为三角波。Vcontrol通过切割三角波来产生占空比:
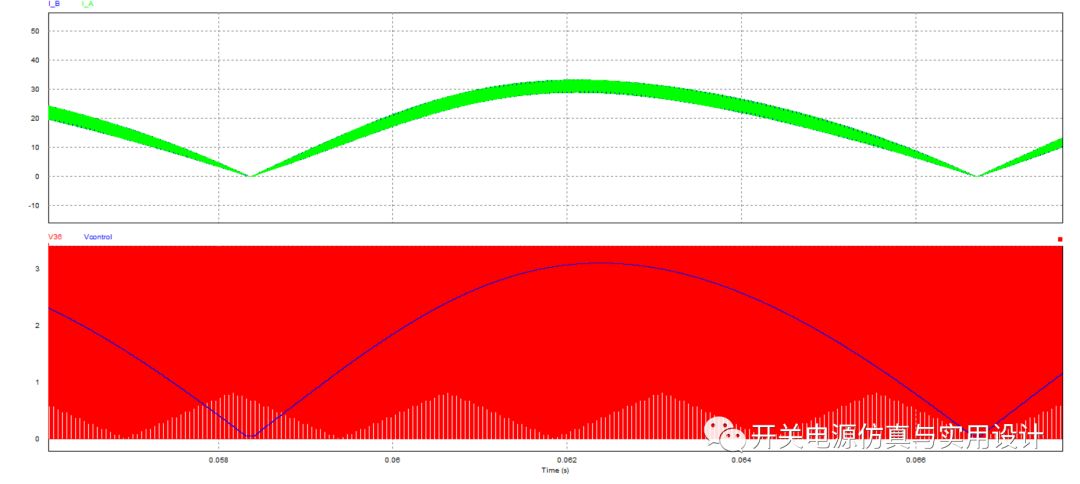
 展开一些看的更清楚,在一个正弦周期内,占空比控制值波形的幅度和相位在跟随正弦电压波形。
展开一些看的更清楚,在一个正弦周期内,占空比控制值波形的幅度和相位在跟随正弦电压波形。
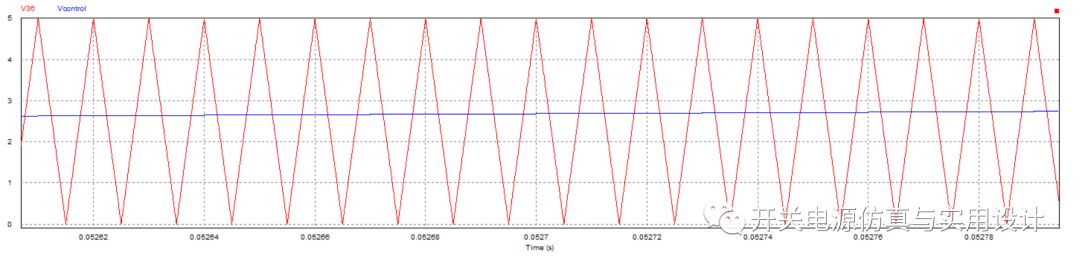
下图可以很容易的看到,占空比控制值切割三角波得到随着正弦周期变化的占空比。
看到这里是不是觉得实现数字单周期的控制算法太简单了,实际效果行不行,THD如何?PF如何?有点不敢相信吧?
请看THD,可以做到小于5%。

PF值也是可以做到99.315%,效果还是非常赞的。

-
 jf_16066267
2025-10-24
0 回复 举报可以分享下电路文件吗 收起回复
jf_16066267
2025-10-24
0 回复 举报可以分享下电路文件吗 收起回复
-
慧能泰双相交错CCM PFC芯片的优势解析2024-07-25 3632
-
基于单周期(OCC)控制的CCM PFC2016-08-11 7982
-
求助 两相交错同步整流BUCK电路输出电压与占空比关系问题?2018-05-02 7200
-
什么是PFC2018-11-28 3612
-
使用C2000 MCU的数控式两相交错LLC谐振转换器设计2018-12-26 2940
-
700W两相交错式功率因数校正转换器含物料清单和原理图2018-12-29 2729
-
具有功耗计量功能的两相交错700W功率因数校正转换器参考设计2022-09-16 1199
-
将主电路的三相电源的任意两相交换对电路有什么影响?2023-04-24 1126
-
单周期控制PFC 电路研究及芯片应用介绍2009-12-07 1330
-
单周期控制连续导电模式PFC原理和应用2011-02-22 1402
-
具有功耗计量功能的两相交错式功率因数校正转换器2022-09-05 705
-
使用 FAN9673 5 kW CCM PFC 控制器的 3 通道交错式 CCM PFC 设计指南2022-11-15 1165
-
交错CRM BOOST PFC仿真(2)2023-06-23 2731
-
单级PFC和交错式PFC介绍2024-02-23 8069
-
UCC28070 两相交错式连续导通模式 (CCM) PFC 控制器2025-04-01 2092
全部0条评论

快来发表一下你的评论吧 !

