

穿越频率,带宽和动态的关系
电子说
描述
开环/闭环函数波特图的关系
为简化问题,以单位负反馈系统为例说明。环路,loop gain,也就是我们常说的"开环传递函数"就是G,整体的闭环传递函数就是T。
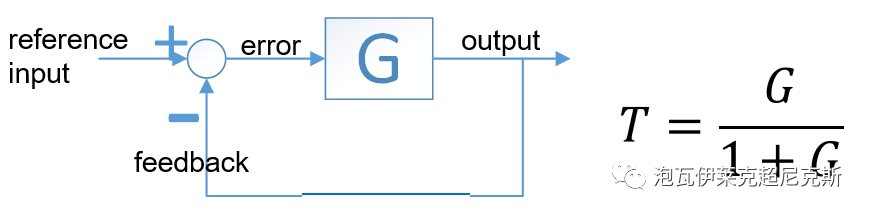
在工程习惯中,G会被直接用来做loop gain环路分析,观察其穿越频率ωc,增益相位裕度GM,PM;而T在基于频域设计的方法论中,很少被直接关注,但T才是最直接反应闭环后,输入输出对应频率特性的。
通过开环函数G的波特图直接设计系统性能,其实是以G间接预估闭环函数T的频率特性,从而完成对T的设计。
(此处概念混淆,以及不清楚为何引入开环传递函数判断闭环系统稳定性的读者,请自行复习“自动控制原理”课本中关于稳定性和频率特性的章节)
以典型一阶和二阶系统展示G和T的关系:


-
结论:
1. G的增益超过0dB(增益大于1)的低频段,由于T=G/(1+G) (注意是复数计算) ,T的增益会接近1(0dB);越低频增益越高,T的增益约接近1(0dB),越能对低频信号实现无误差地跟踪。
2. 0dB以下的高频段,G的增益越低,那么T对应的增益也会越低。
3. G的相位体现在 T=G/(1+G) 的复数计算中,相位偏移较多时,有可能在T的该频段造成谐振峰.
穿越频率和带宽的关系
回顾定义如下:
- 开环截止频率ωc也称为穿越频率(crossover frequency),是开环G幅频特性曲线穿越0dB(增益=1)时,对应的频率;
- 闭环截止频率ωb也称为带宽频率(bandwidth),是闭环T幅频特性下降到-3dB(增益=1/根号2)时,对应的频率。
那么两者的关系,推导如下:(注意在带宽ωb附近,一般的控制系统都有积分环节存在(如PI),G的相角在-90°-180°,故G中α(ωb)<0成立)


- 结论:
稳定的负反馈系统,开环系统的穿越频率和闭环系统的带宽很接近,存在ωb>ωc且有同向性。工程上近似时,时常把两者直接混用。
带宽和动态: 窥一斑,能否见全豹?
由闭环系统T的带宽推测动态性能最为直观:带宽越高,越多频率分量的信号放大增益在-3dB以上,可以被有效跟踪,因此动态性能越好。但是,尤其注意以下:
- 结论:
穿越频率/带宽描述的仅仅是频域上一个点的信息,是“窥一斑而见全豹”的做法, 仅可当作指导性的规律揭示, 并不能直接用于比较两个系统的动态!
动态响应由全频率段的幅频/相频特性共同决定。

给出如下例子,让我们加深对带宽和动态关系的理解。
- 例子1: 带宽小的 系统1 ,动态反而快于带宽大的 系统2 !!!
究其原因,正是因为恰在带宽附近的频段,系统2的增益高于系统1,但在其他频段,系统1的增益均高于系统2。

- 例子2:相同的带宽和低频增益,导致从0到1的建立时间近似相同,但由于高频增益不同,动态响应的速度完全不同(期间的凹凸特性):

- 例子3:相同的带宽和高频增益,但由于低频增益谐振峰的不同,动态响应的速度完全不同(包括超调):

那么,“带宽越大,动态越快” 这个结论是怎么来的?
- 例子4:相同的系统结构(频率特性的全局分布一致),带宽越高,动态越快:

可以看到,当且仅当你要做比较的若干个系统,其有相同(或相近)的系统结构,也即频率特性的全局分布一致(或类似)时,才有老生常谈的这句经典传说,被奉为圭臬。
当设计环路的补偿器时,我们在尽可能提高带宽的同时,不可能再刻意压低其他部分频段的增益,因此,用这句话作指导性的设计方向仍然是有意义的。
-
PLL中滤波器带宽和环路带宽的关系是什么?2021-06-24 2992
-
如何用MATLAB进行仿真得出信噪比,带宽和信道容量的关系2021-08-17 2039
-
谈一谈对穿越频率的理解2021-11-17 4664
-
带宽和增益带宽,带宽的种类,带宽是什么意思2010-03-22 6857
-
LoRa的带宽、频率测试2018-04-27 13648
-
一文看懂载波频率和带宽的关系2018-03-13 66294
-
带宽和数据传输速率有什么关系2021-02-12 48559
-
介质滤波器带宽和频率关系大吗_介质滤波器调试2023-02-27 1531
-
如何区分模拟带宽和数字实时带宽?2023-09-11 2785
-
运放带宽与增益的关系是什么?2023-09-17 6239
-
示波器带宽与探头带宽的关系揭秘2024-01-22 2674
-
示波器带宽与采样率的关系2024-05-17 7928
-
频谱仪分辨率带宽和视频带宽的关系2024-06-03 2739
-
固定带宽与动态带宽的区别2024-12-06 1855
-
调制频率与带宽之间的关系2025-01-21 4053
全部0条评论

快来发表一下你的评论吧 !

