波特图中增益裕量GM和相位裕量PM的由来

这一篇我们来谈其他两个热门指标，老生常谈的稳定裕量：

增益裕量 Gain Margin，以下简称GM

相位裕量 Phase Margin，以下简称PM

系统到底有多稳定？

• 系统的时域响应，收敛还是发散→反应 绝对稳定性 （稳定还是不稳定）
• 系统的时域响应，收敛的平稳度→反应 相对稳定性 （稳定裕量有多大）

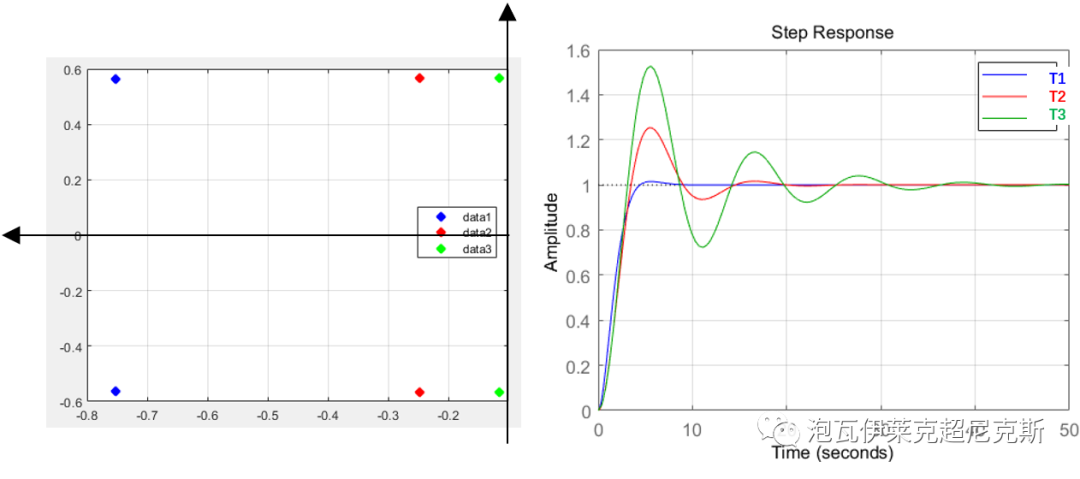
根据劳斯判据，三个闭环典型二阶系统T1,T2,T3，如下图所示，闭环系统特征方程的根都位于左复半平面，因此都是绝对稳定的。

但是，显然其相对稳定性T1>T2>T3。反应在闭环系统特征方程的根的分布上，即距离虚轴（临界区域）越远的，越难振荡，相对稳定性越好。

换句话说，系统****有多稳定，即相距绝对稳定的临界区域的距离，有多远。

波特图中GM和PM的由来

我们常用开环函数loop gain的频率特性，来预测和评估闭环系统的性能，因此闭环系统的极点距离临界区域的距离，得想办法转换到开环函数loop gain的频域指标上，才可以方便地指导设计。这就是导出波特图中GM和PM的出发点。

为了导出GM和PM，我们必须先回到开环函数loop gain的奈奎斯特图（Nyquist曲线，即频域中增益和相角的极坐标，随频率变化的轨迹）。

注：引入极坐标和奈奎斯特图，从而在频域判断线性系统的稳定性的原因，可以自行回顾“自动控制原理”劳斯判据，柯西幅角原理，辅助方程和平面映射等基本内容。

奈奎斯特图和波特图只是在频域的不同表现形式：上述三个闭环典型二阶系统，其开环函数G1,G2,G3的波特图(0+→+∞)和奈奎斯特图(-∞→0-→0+→+∞)，两者对应的关系如下。

注：奈奎斯特曲线总是按照(-∞→0-→0+→+∞→-∞...)这个循环形成包围曲线，如下所示。

针对工程实际中最常见的开环函数，一般不含有右半平面极点，本身往往是绝对稳定的，只是动态特性欠佳，需要补偿和校正。

这样的开环函数特性，根据奈奎斯特稳定判据，它的奈奎斯特曲线顺/逆时针包围(-1，j0)的正负和要为0，则有如下：

• 结论：

一般/常见的****稳定系统，其闭环函数特征方程的根，在左半平面相距临界区域（虚轴）的远近，对应了开环函数loop gain奈奎斯特曲线，相距(-1,j0)这个临界点的远近。

以一般/常见形状的开环系统对应的奈奎斯特图为例，可以看到，当奈奎斯特曲线通过增益放大或顺时针旋转的方式，都会造成包围(-1，j0)，从而不再满足奈奎斯特稳定性判据。

为了 达到不稳定的临界点而允许放大的增益，和允许顺时针旋转的角度，可作为衡量闭环系统相对稳定性高低的指标，即开环函数loop gain的GM和PM 。

PM对动态的影响

真实的工程实践中，开环函数几乎都是高阶系统。

时域响应波形中我们所关心的形状和对应频率段，都可被一个主导二阶系统近似。这对主导极点的时域响应，可近似该频段的时域响应的大致形状。

故我们仍以典型闭环二阶系统的开环函数为例：阻尼比ξ是影响振荡程度的关键参数。从时域响应来看，阻尼比ξ越大，代表系统的稳定性越好。

闭环二阶系统中，阻尼比ξ恰可以与开环函数的相位裕量PM对应，直接建立函数关系：

• 结论：

针对典型二阶系统主导的闭环系统，其开环函数loop gain的相位裕量：

• PM≤60°时，阻尼比ξ**≈0.01PM<0.6，PM越低，系统超调越大；**

  注：特别的，PM=45°，阻尼比ξ≈0.45，系统超调<20%尚可接受，可作为PM>45°准则的理论支撑。

• PM>60°时，0.6<阻尼比 ξ <0.01PM ，几乎不再有超调。

GM对动态的影响

对于GM来说，设计者的初衷并非只针对这一个频率点，这和上一节所讨论的穿越频率/带宽的内涵是一致的。

GM设计得大，其本意是希望相位=-180°的高频之处，以及更高的高频频段整体，系统能有足够大的增益衰减，以抑制环路中的高频噪声。

然而，GM和系统其他参数无法解耦， 通过补偿器使高频频段整体进一步增益衰减，势必会带来更多的相位延迟，导致在相对较低的频率就穿越-180°，从而表现出更小的GM。因此，单独探讨和比较GM的大小，没有特别的意义。

• 结论：

设计开环函数loop gain的补偿器时，应优先保证穿越频率和PM尽量满足期望，增益裕量不至过小即可。