

如何直观地判断两级放大器的零点位置呢?
电子说
描述
Razavi教授在他的CMOS模拟IC设计教科书中介绍了米勒补偿的两级放大器,这是一个很经典的结构,里面有很多问题可以分析。可以毫不过分地说,看一个人对模拟IC设计的理解水平,首先就应该问他对两级放大器的细节理解程度。
一个初学者通常会有的疑惑是:如何直观理解两级放大器采用Rm电阻串接Cc后,零点从右半平面移动到左半平面?
本文旨在解决上述问题,接下来将会做如下两件事:
①给出一种直观地判断两级放大器零点位置的方法,具体讲就是直观看出零点是左半平面还是右半平面的方法;
②将我们发展出的零点判定方法使用在其它更复杂的结构上以进一步验证这种方法。
先说明①
首先必须承认一个事实:若在两个电压端点之间存在不止一条路径,则该电压传递函数中存在零点。在实际电路设计中,“不止一条路径”通常指的是两条路径。
如果考虑一个五管差分对,会发现镜像零点带来的是左半平面零点(LHPZ)。这是因为五管差分对的差分输入信号汇聚到输出有两条路径,并且它们最终在输出是同相叠加的。不可能反相叠加,因为这不符合放大器的定义。那么也就是说,同相叠加的信号路径将会形成左半平面零点(LHPZ)。
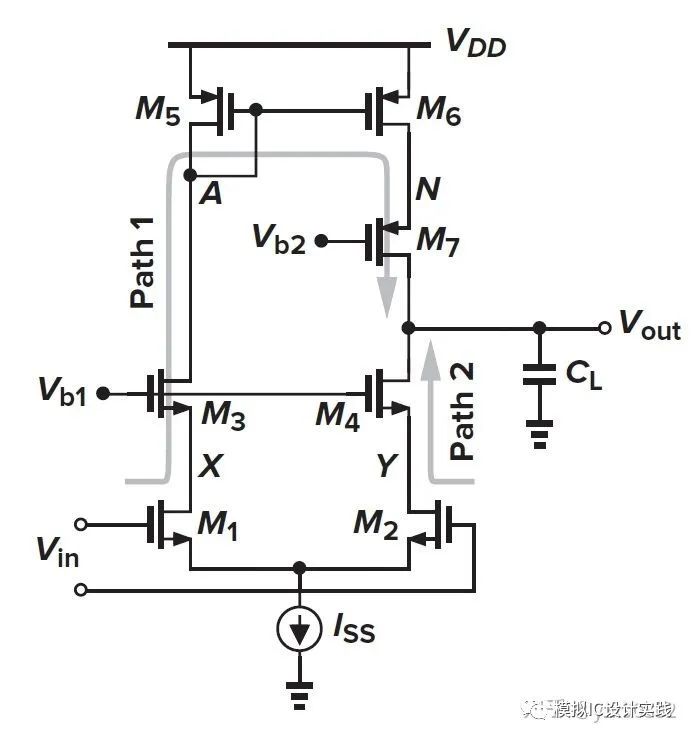
图1 一个五管差分对以及它的信号路径
现在考虑米勒补偿的两级放大器,单独看它的第二级就可以分析出零点是右半平面的
。这就是我们需要首先分析的问题:如何直观理解这个右半平面零点?

图2 一个米勒补偿的两级放大器
直观理解右半平面零点是容易的。考虑高频下,Cc几乎将第二级的输入和输出短接,原本在低频下,他们的极性是相反的,但是现在由于短接极性似乎被强迫为同相,这就造成了右平面零点。或许这么讲还是不太清楚,再考虑如下例子就会更加清楚:
将第二级的Cc替换成电阻Rm。当Rm=0时,第二级的输入和输出被强迫为同相;当Rm= ∞时,输入输出被隔离,维持反相。因此中间必然存在一个Rm,使得这种同相反相存在突变点(类似于高中所学的零点存在性定理)。稍微进行电压增益分析会发现这个分界点就是 直观地判断两级放大器零点位置
。在这个分界点的左右,就分别对应着左平面和右平面零点。
也就是说,高频信号同相叠加,则零点为左平面;高频信号反相叠加,则零点为右平面。目前为止,这个逻辑适合于五管差分对的电流镜负载和两级放大器的简单米勒补偿/串联电阻补偿。因此①的目的达到了。
然后说明②
上面的直观判断放大器零点位置的理论应该被更复杂的结构验证。比如下面的NMC三级放大器,是一个常用的低效率补偿结构,我们刚刚发展出来的的理论也应该适用它。

图3 一个NMC补偿的三级放大器
根据我们的理论,首先判断NMC结构中的双路结构:分别有红色和蓝色两组,这对应了开环传递函数中的两个零点。注意跨导的符号就是增益的符号,蓝色在高频处为反相叠加;红色在高频处为正向叠加。因此蓝色代表右平面零点,红色代表左平面零点,整个放大器的零点为一左一右。

图4 一个NMC补偿的三级放大器的信号流
根据严格的分析,三级放大器的传递函数为

可见分子是一个开口向下的二次函数,必然有实根,且一左一右,验证了我们的理论。那么,是否还能验证其它的结构呢?
-
两级共射极放大器组成的宽频放大器2014-08-18 4869
-
利用电路的自然响应来说明极点和零点位置的影响2020-09-27 2884
-
一文搞懂电路的极点和零点2022-02-17 30378
-
两级功率放大器静态偏置点的研究2009-12-14 577
-
公共屏极电源的两级放大器电路2009-01-12 948
-
CMOS两级运算放大器调零电路性能分析2009-10-30 5814
-
放大器极零点与频率响应2013-09-04 682
-
利用电路的自然响应说明极点/零点位置的影响2019-01-04 1413
-
提高两级放大器增益的方法有哪些?2023-09-18 6032
-
如何调节通用放大器的零点?2023-09-19 2540
-
编码器零点位置怎么看 | 编码器零位怎样确定2024-02-18 4636
-
方向角度传感器零点位置怎么判断2024-07-22 1608
-
放大器级数越多零点漂移越严重吗2024-08-06 1785
-
交流放大器存在零点漂移吗2024-09-26 1182
-
放大器零点漂移主要原因_放大器零点漂移怎么调2024-10-25 4155
全部0条评论

快来发表一下你的评论吧 !

