基于高非线性光纤中前向布里渊散射的增强型声阻抗传感以及温度和应变同时传感技术

01 导读

1.1 基于高非线性光纤中前向布里渊散射的声阻抗传感技术

基于布里渊散射的光纤传感系统能进行长距离、分布式地测量。然而在基于后向布里渊散射的分布式光纤传感系统中，光场和纵向声波均被束缚在纤芯中传播，因此可以测量的物理量也局限于温度、应变以及振动等，而无法对光纤外部的物质进行探测。另一方面，光纤中除了后向布里渊散射外，光纤中还存在前向布里渊散射。利用前向布里渊散射（FBS）中的横向声波可以对光纤外界物质的声阻抗进行测量，进而实现光纤外部物质探测。然而标准单模光纤（SSMF）中前向布里渊散射的增益较小，使得信号信噪比较差，导致基于SSMF的声阻抗传感灵敏度较低，难以实现高灵敏度的外界物质探测。

针对上述问题，华中科技大学唐明教授、王亮教授团队提出了一种基于高非线性光纤（HNLF）中前向布里渊散射的高灵敏度声阻抗测量技术。通过仿真证明了HNLF中径向声模式（R0，m）引起的FBS相比于SSMF中的FBS具有更高的增益系数和散射效率，这为声阻抗测量提供了更好的信噪比及更高的传感灵敏度。实验中测得HNLF中模式的声阻抗灵敏度为3.83MHz/［kg/（s·mm2）］，比SSMF中增益几乎最大的R0，9模式的2.70MHz/［kg/（s·mm2）］高了1.42倍。同样对HNLF中TR2，5模式进行声阻抗测量，其灵敏度为0.24MHz/［kg/（s·mm2）］，比SSMF中相同模式的灵敏度高了1.5倍。研究成果以“High-sensitivity acoustic impedance sensing based on forward Brillouin scattering in a highly nonlinear fiber”为题发表在Optics Express期刊上。华中科技大学硕士研究生曾柯谚为论文第一作者，王亮教授为论文通讯作者。

1.2 基于高非线性光纤中前向布里渊散射的温度和应变同时传感

布里渊光纤传感器因其出色的温度和应变传感能力而引起了广泛的研究兴趣。不过布里渊光纤传感器大多是基于后向布里渊散射（BBS），其中布里渊频移（BFS）与温度和应变均线性相关。然而，BFS存在温度和应变的交叉敏感性，使得温度和应变的同时测量变得困难。目前已经提出了多种解决方案来实现双参量同时测量，其中使用具有多峰布里渊增益谱（BGS）的光纤可以算作温度及应变同时测量中最有效且简单的方法之一。然而，由于BBS的BFS通常在~10GHz左右，因此需要频率范围达到~10GHz的微波源进行测量，这使得实验装置的成本增高。此外，由于BGS的线宽相对较宽（几十MHz），在提取BGS的BFS时，不仅需要更多的频率扫描次数，而且测量误差也相对较大。

针对上述问题，华中科技大学唐明教授、王亮教授团队提出了一种基于高非线性光纤（HNLF）中前向布里渊散射（FBS）的增强型温度及应力同时传感技术。方案利用HNLF中的FBS首次实现了温度和应变同时传感。原理是利用了径向声模式R0，m和扭转-径向声模式TR2，m对于温度和应变的不同响应。为了提高测量灵敏度，我们选择了在HNLF中具有较大FBS增益的高阶声模式用于测量。进一步地，为了减小测量误差，我们提出了一种选择最佳模式组合的方法，该组合具有最小测量误差，并通过仿真和实验进行了验证。工作中选择了三种模式组合进行温度和应力的同时测量，通过模式组合选择方法，通过（R0，18， TR2，29）实现了最低的温度和应变误差0.12°C/39µε。与基于BBS的传感器相比，该方案只需要测量1GHz左右的频率，不需要~10GHz的微波源，有效降低了系统成本。此外，FBS的谐振频率和谱线宽度都比BBS小得多，也有效提高了测量精度。研究成果以“Simultaneous Sensing of Temperature and Strain with Enhanced Performance using Forward Brillouin Scattering in Highly Nonlinear Fiber”为题发表在Optics Letters期刊上。华中科技大学博士研究生杨贵江为论文第一作者，王亮教授为论文通讯作者。

02 研究背景

2.1 基于高非线性光纤中前向布里渊散射的声阻抗传感技术

近年来，FBS技术的应用使其能够根据测量的声阻抗来识别光纤外物质的环境检测。由于横波的参与，基于FBS的传感器可以测量光纤外物质的声阻抗，而不需要特殊的结构，使用普通光纤即可完成。但是标准单模光纤（SSMF）中FBS增益较弱，声阻抗传感的灵敏度较低。

为解决上述问题，本团队提出基于HNLF中FBS进行声阻抗传感，首次演示了灵敏度超过3MHz的声阻抗传感。得益于高声光耦合效率，HNLF中R0，m和TR2，m诱导的FBS都比SSMF具有更大的增益系数和散射效率。这提供了更好的信噪比（SNR），因此更大的测量灵敏度。通过在HNLF中使用R0，20模式，我们获得了3.83MHz/［kg/（s·mm2）］的更高灵敏度，而在SSMF中使用R0，9模式（几乎具有最大的增益系数）测量时的灵敏度为2.70MHz/［kg/（s·mm2）］。同时，在HNLF中使用TR2，5模式时，测量到的灵敏度为0.24MHz/［kg/（s·mm2）］，仍然是在SSMF中使用相同模式时的1.5倍。灵敏度的提高将使基于FBS的传感器对外部环境的检测更加准确。

2.2 基于高非线性光纤中前向布里渊散射的温度和应变同时传感

对于基于BBS的温度及应变传感器，由于需要频率范围达到~10GHz的微波源进行测量，使得系统成本很高。并且线宽较宽（几十MHz）的BGS也使得频率扫描过程耗时较长，且从BGS中提取BFS时也会产生较大的测量误差。另一方面，对于前向布里渊散射（FBS），它是由入射光场与光纤中横声波场相互作用而产生的，通常其共振频率在几十MHz到1GHz左右，谱线线宽为几MHz，都比BBS小得多。因此，使用基于FBS的传感器进行温度和应变传感不仅可以降低测量成本，而且还可以提高传感精度。但FBS中仍存在温度与应变的交叉敏感性。最近，L.A.SÁNCHEZ等人在长周期光栅中使用FBS来区分温度和应变。但是，这种光栅需要改变光纤结构，不适合分布式传感。

为解决上述问题，本团队首次提出并展示了使用HNLF中的FBS效应来实现温度和应变的同时测量，其较大的高频增益增强了传感性能。并且我们提出了一个理论误差模型，帮助选择最佳的模式组合，实现最小的测量误差。实验中采用三种模式组合进行展示，其中基于模式组合（R0，18， TR2，29 ）获得了最低温度和应变误差0.12℃和39µε。与基于BBS的传感器相比，该方法只需要在~1 GHz范围内进行测量，可以用更便宜的设备实现高精度测量。此外，FBS增益谱的窄线宽也提高了传感精度。

03 创新研究

3.1 基于高非线性光纤中前向布里渊散射的声阻抗传感技术

本工作使用了基于光纤萨格纳克环的实验装置，用于测量FBS频谱并演示基于HNLF的高灵敏度声阻抗传感，如图1所示。激光器输出波长为1550.12 nm的入射光，经过光纤隔离器后被掺铒光纤放大器放大光功率，随后经过一个光纤滤波器用于滤除掺铒光纤放大器引起的自发辐射噪声，之后进入萨格纳克环中。其中，萨格纳克环包括一个50：50光纤耦合器，一个偏振控制器以及待测光纤。在待测光纤内，泵浦光将激励横向声波，并通过调整环内的偏振控制器，可以激励或者抑制R0，m模式和TR2，m模式，同时也可以将声学模式引起的相位调制转换为强度调制，最终和反向传播的光在耦合器处干涉输出。拍频信号由1.5 GHz的探测器接收，并在电频谱分析仪上显示前向布里渊散射的频谱信号。

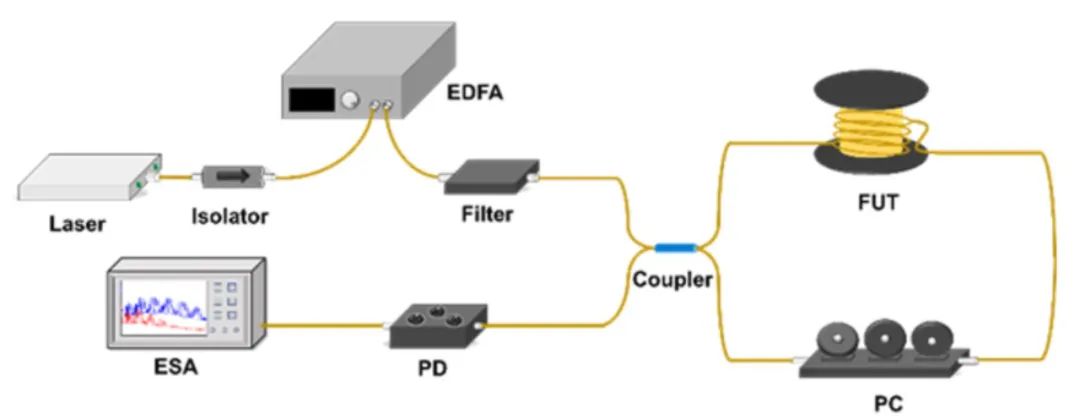
图1 利用FBS测量光纤外界声阻抗的实验装置图

图源： Optics Express （2023）。

https://doi.org/10.1364/OE.483085 （Fig. 5）

实验中使用的HNLF的纤芯直径为4.45，包层直径为127，模场直径为3.3且HNLF的光纤损耗小于1.5 dB/km。图3（a）和（b）分别展示了940 m长的HNLF （蓝色）中R0，m模式和TR2，m模式1.5 GHz范围内的FBS增益谱。作为对比，同样测量了1 km的SSMF（红色）中对应的FBS增益谱。为了比较公平，对EDFA的输出功率进行调整，以保证通过SSMF后的光功率与通过HNLF后的光功率一致。如图2（a）所示，由于HNLF较高的增益系数，当共振频率超过1.2 GHz时，其R0，m模式的共振峰值仍然很高。相反地，当共振频率超过800 MHz时，图2（a）中SSMF的共振峰就几乎消失。同样对于TR2，m模式来说，HNLF在较宽的频率范围内都有更强的共振峰值，而SSMF中共振峰在超过500 MHz的范围外就几乎消失了。如果将图2（a）中HNLF和SSMF测得的结果基线设置为同一水平线，将发现HNLF的最大功率比SSMF中大3 dB以上。不同的基线是由于HNLF和SSMF使用了不同的泵浦光功率来补偿光纤的损耗，以便进行公平的比较。

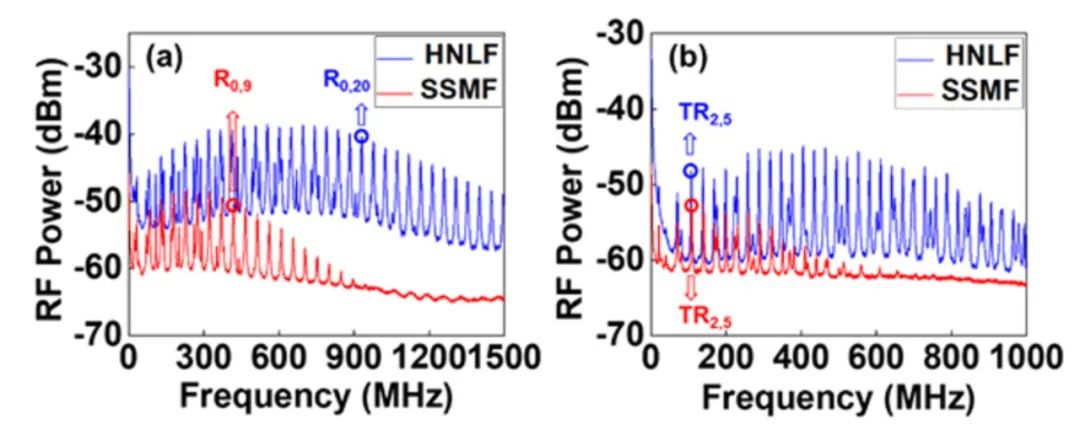
图2 HNLF（蓝色）和SSMF（红色）中：（a） R0，m模式和（b） TR0，2m模式对应的FBS增益谱

图源： Optics Express （2023）。

https://doi.org/10.1364/OE.483085 （Fig. 6）

对于声阻抗传感实验，由于光纤的丙烯酸酯涂覆层的损耗较高，会对测量结果造成影响，因此在实验中，选取了一段10m去除涂覆层的HNLF作为待测光纤，并将光纤置于0%~40%浓度的蔗糖溶液中（0%浓度对应纯水）。注意到，当蔗糖溶液的浓度低于50%时，其溶液浓度与溶液的声阻抗呈现线性关系。选择了R0，20模式对应的FBS增益谱进行声阻抗的测量，因其能避免其余TR2，m模式的串扰，并且其几乎为增益最大的模式。将HNLF置于不同外界物质中测量得到的FBS增益谱如图3所示。图3（a）展示了去除涂覆层的HNLF置于空气中的FBS增益谱，并作为参考，R0，20模式峰值旁的小峰是由TR2，49模式的不完全抑制引起的。通过对测得的FBS增益谱进行洛伦兹曲线拟合，可以得到不同环境下的FBS增益谱线宽，当HNLF置于空气中时，其线宽为1.60 MHz。测量的线宽的值比仿真中的值稍大，可能是光纤包层的不均匀性所导致。纯水时，图3（b）对应的FBS增益谱的线宽为4.76 MHz。对比空气中测量的结果，光纤置于纯水中会导致线宽显著变宽，且由于外界物质的声阻抗的变化，光纤包层和外界物质边界处的声反射率也随之变化，声波反射能量减小，信号强度降低。图3（c）-（f）分别展示了溶液浓度为10% ~ 40%（10%浓度间隔）时测量的FBS增益谱，且拟合后计算出对应的线宽分别为5.01 MHz、5.76 MHz、6.05 MHz和6.66 MHz。可以看到，随着蔗糖溶液的增加，增益谱的线宽也随之增加R0，20模式的共振频率为930.7 MHz。图3（g）绘制了不同浓度的蔗糖溶液的声阻抗与测量的线宽的关系。通过线性拟合，HNLF中R0，20模式的声阻抗灵敏度为3.83±0.19MHz/［kg/（s·mm2）］。我们也利用了HNLF中的其他声学模式进行了声阻抗传感实验，结果如图4（a）-（c）所示。当使用HNLF中R0，19、R0，20和R0，21模式时，对应的灵敏度分别为3.70±0.15MHz/［kg/（s·mm2）］、3.73±0.21MHz/［kg/（s·mm2）］和3.68±0.22MHz/［kg/（s·mm2）］。可以看到相邻模式的声阻抗灵敏度有微小的差异。

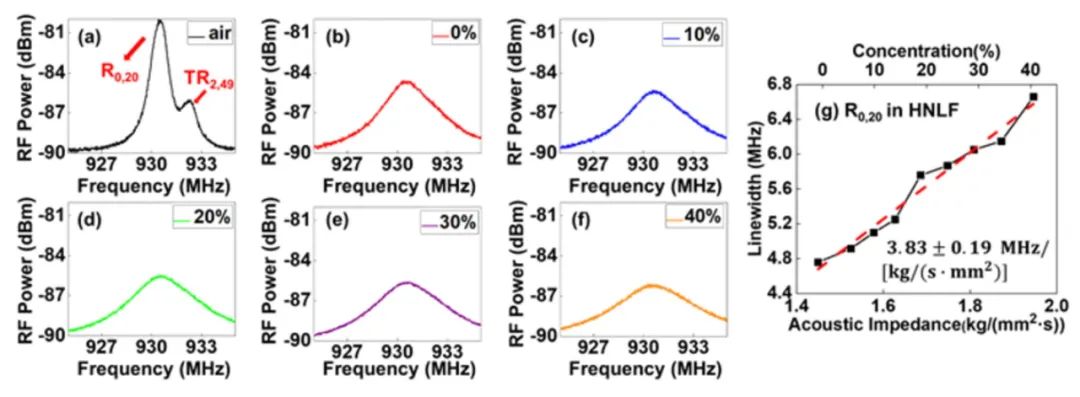
图3 利用HNLF在不同外界物质情况下测量的R0，20模式增益谱：（a） 空气；（b） 0%；（c） 10%；（d） 20%；（e） 30%；（f） 40% 浓度的蔗糖溶液；（g） FBS线宽随声阻抗的变化关系

图源： Optics Express （2023）。

https://doi.org/10.1364/OE.483085 （Fig. 7）

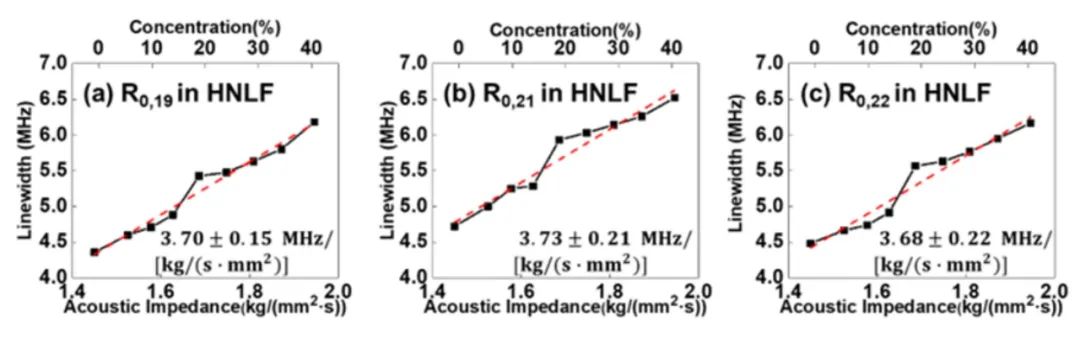
图4 利用HNLF中不同声模式测得的FBS增益谱线宽随声阻抗的变化：（a） R0，19；（b） R0，21；（c） R0，22

图源： Optics Express （2023）。

https://doi.org/10.1364/OE.483085 （Fig. 8）

作为对比，将一段去除涂覆层的10m SSMF作为待测光纤进行相同的声阻抗传感测量。测量过程中，选取了增益几乎最大的R0，9声模式对应的FBS增益谱。不同环境下的FBS增益谱如图5（a）-（f）所示，其中图5（a）对应SSMF置于空气中的结果，计算出对应的线宽为0.60 MHz，图5（b）-（f）分别对应0% ~ 40%浓度的蔗糖溶液，拟合后的线宽分别为4.03 MHz、4.40 MHz、4.74 MHz、5.00 MHz和5.43 MHz。R0，9模式的共振频率为417.8 MHz。通过线性拟合，SSMF中R0，9模式的声阻抗灵敏度为2.70±0.13MHz/［kg/（s·mm2）］，如图5（g）所示。同样对SSMF中R0，7和R0，8模式进行了相同的测量，这两个声学模式对应的声阻抗灵敏度分别为2.46±0.13MHz/［kg/（s·mm2）］和2.21±0.12MHz/［kg/（s·mm2）］，如图6（a）和（b）所示。由于在SSMF中，R0，5模式和TR2，21/TR2，22模式之间的频谱有很大的重叠，因此没有选取R0，5模式进行传感实验。通过对比图3-4以及图5-6，相比于SSMF，利用HNLF可以实现超过3MHz/［kg/（s·mm2）］的声阻抗灵敏度。

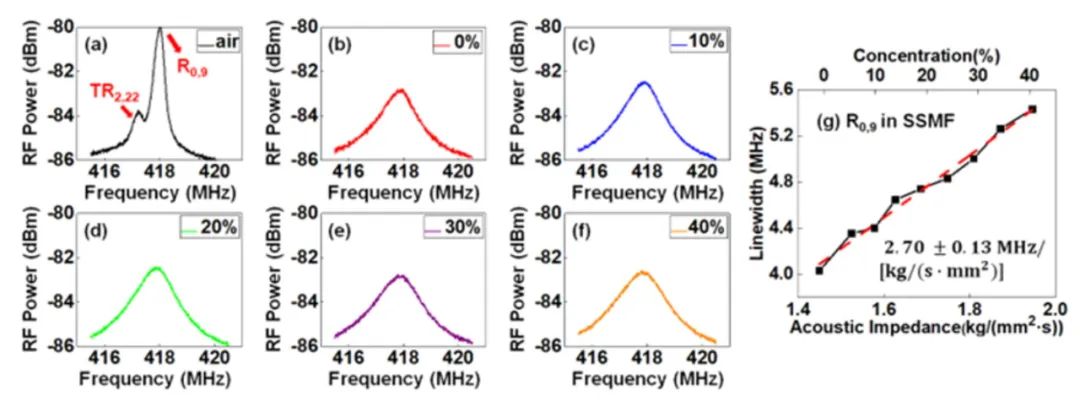
图5 利用SSMF在不同外界物质情况下测量的R0，9模式增益谱：（a） 空气；（b） 0%；（c） 10%；（d） 20%；（e） 30%；（f） 40% 浓度的蔗糖溶液；（g） FBS线宽随声阻抗的变化关系

图源： Optics Express （2023）。

https://doi.org/10.1364/OE.483085 （Fig. 9）

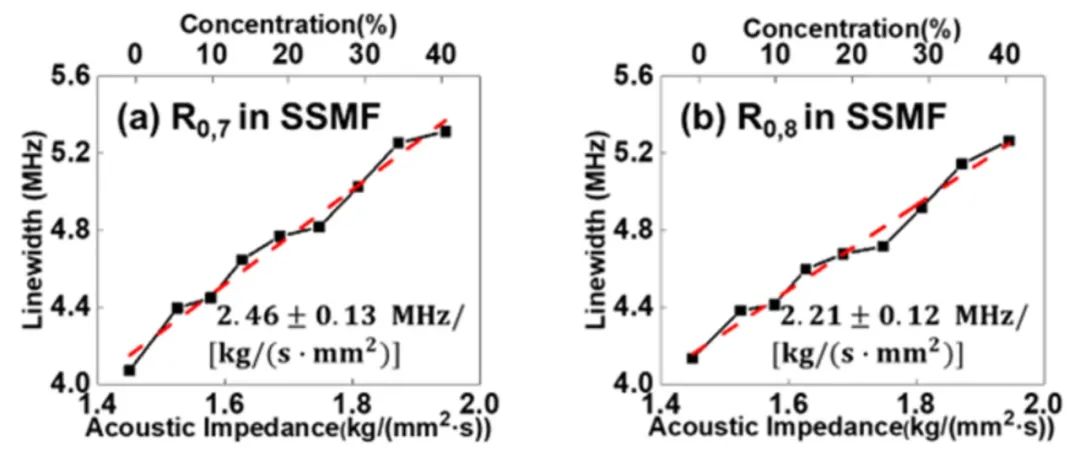
图6 利用SSMF中不同声模式测得的FBS增益谱线宽随声阻抗的变化：（a） R0，7；（b） R0，8

图源： Optics Express （2023）。

https://doi.org/10.1364/OE.483085 （Fig. 10）

最后我们也利用HNLF中TR2，m模式进行了声阻抗传感实验。实验中选择了TR2，5声模式（共振频率为106.9 MHz）进行声阻抗的测量。TR2，5模式可以避免R0，m模式的串扰，且散射效率为0.51，仍然保持较好的水平。实验结果如图7所示。图7（a）展示了HNLF置于空气中的结果，且拟合得到的线宽为0.13 MHz。图7（b）-（f）展示了不同浓度的蔗糖溶液中测量得到的FBS增益谱，拟合得到的线宽分别为0.23 MHz、0.25 MHz、0.27 MHz、0.30 MHz和0.35 MHz。通过线性拟合可以得到线宽随声阻抗的变化，且HNLF中模式的声阻抗灵敏度为0.24±0.1MHz/［kg/（s·mm2）］，如图7（g）所示。而SSMF中相同声模式的灵敏度为0.16MHz/［kg/（s·mm2）］ ［51］，因此利用HNLF可以将TR2，m模式声阻抗的灵敏度提高1.5倍。

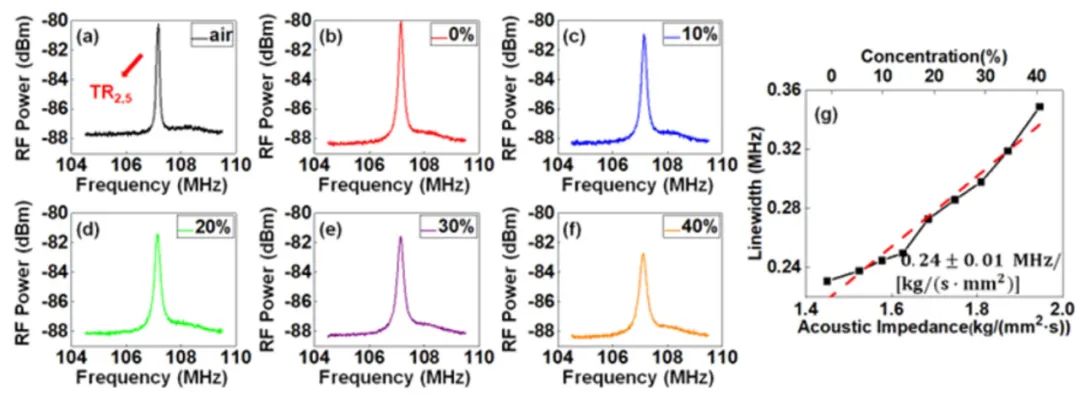
图7 利用HNLF在不同外界物质情况下测量的TR2，5模式增益谱：（a） 空气；（b） 0%；（c） 10%；（d） 20%；（e） 30%；（f） 40% 浓度的蔗糖溶液；（g） FBS线宽随声阻抗的变化关系

图源： Optics Express （2023）。

https://doi.org/10.1364/OE.483085 （Fig. 11）

3.2 基于高非线性光纤中前向布里渊散射的温度和应变同时传感

光纤内FBS的横向声模可分为R0，m和TR2，m两类模式。对于高阶声场模式，其共振频率与温度和应力呈现线性相关，其中R0，m和纵波声速VL线性相关，TR2，m则与横波声速VS线性相关。因此，R0，m和TR2，m的共振频率将对温度和应力具有不同的线性响应。本工作即是通过两者的不同响应系数（1）构建方程组以同时求解温度和应力，表达式如下：

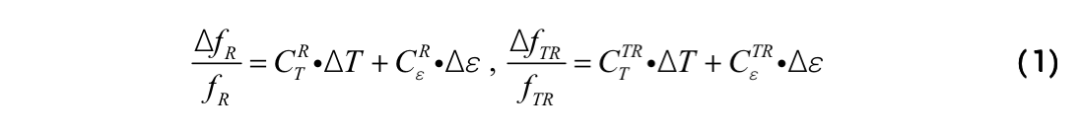
其中，fR和fTR是光纤处于室温且零应力下的谐振频率，作为参考频率；CR T（CTR T）和CR ε（CTR ε）是R0，m（TR2，m）的相对温度系数和应变系数。此时温度和应力的测量误差则可以表示为：

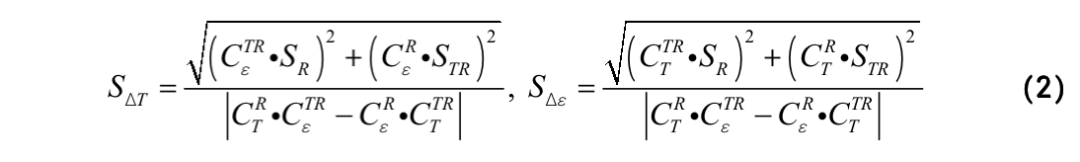
其中，SR 和STR分别表示ΔfR/fR 和ΔfTR/fTR的标准差。并且由于FBS增益谱为洛伦兹型，因此SR 和STR可以进一步写为：

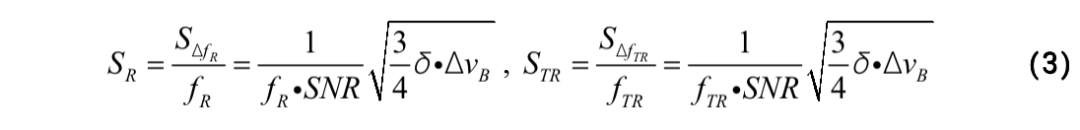
其中，SNR， δ和ΔνB分别表示FBS频谱的信噪比，频率间隔以及线宽。从式（2）和（3）可以得到，高共振频率、高信噪比和窄线宽是实现低测量误差的理想条件。但高共振频率的FBS频谱由于增益小，信噪比通常较低，特别是在标准单模光纤中，高共振频率下的FBS增益几乎为零。因此，单纯采用高频声学模式并不能保证测量误差最小，需要在信噪比和共振频率之间进行权衡。

由于不同声模对温度和应变的响应不同，所以不同的模式组合会产生不同的测量误差。为了选择最佳的模式组合以实现最小的测量误差，本工作分析了HNLF中声学模式的前向布里渊散射效率。图8显示了我们的HNLF在0-1.5GHz频率范围内R0，m和TR2，m模式的归一化散射效率。可以看到，在HNLF中，即使在1GHz以上的高频下，R0，m和TR2，m仍然具有较高的散射效率，在更宽的频率范围内获得更大的FBS增益。但是当频率变高时，散射效率仍会降低，从而降低了SNR。基于散射效率和式（2）和（3）可以分析不同模式组合下的理论温度和应变误差，如图9所示。

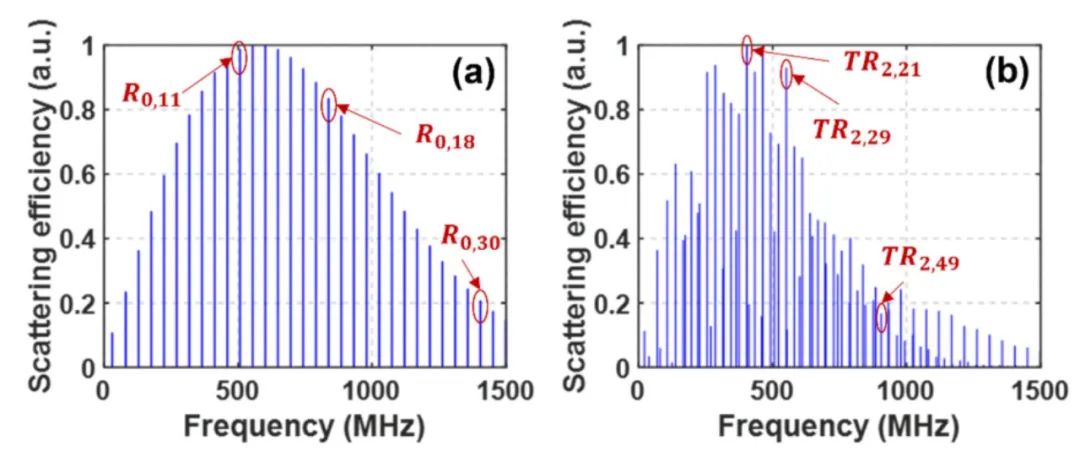
图8 （a） R0，m和 （b） TR2，m模式的归一化散射效率

图源： Optics Letters （2023）。

https://doi.org/10.1364/OL.493637 （Fig. 1）

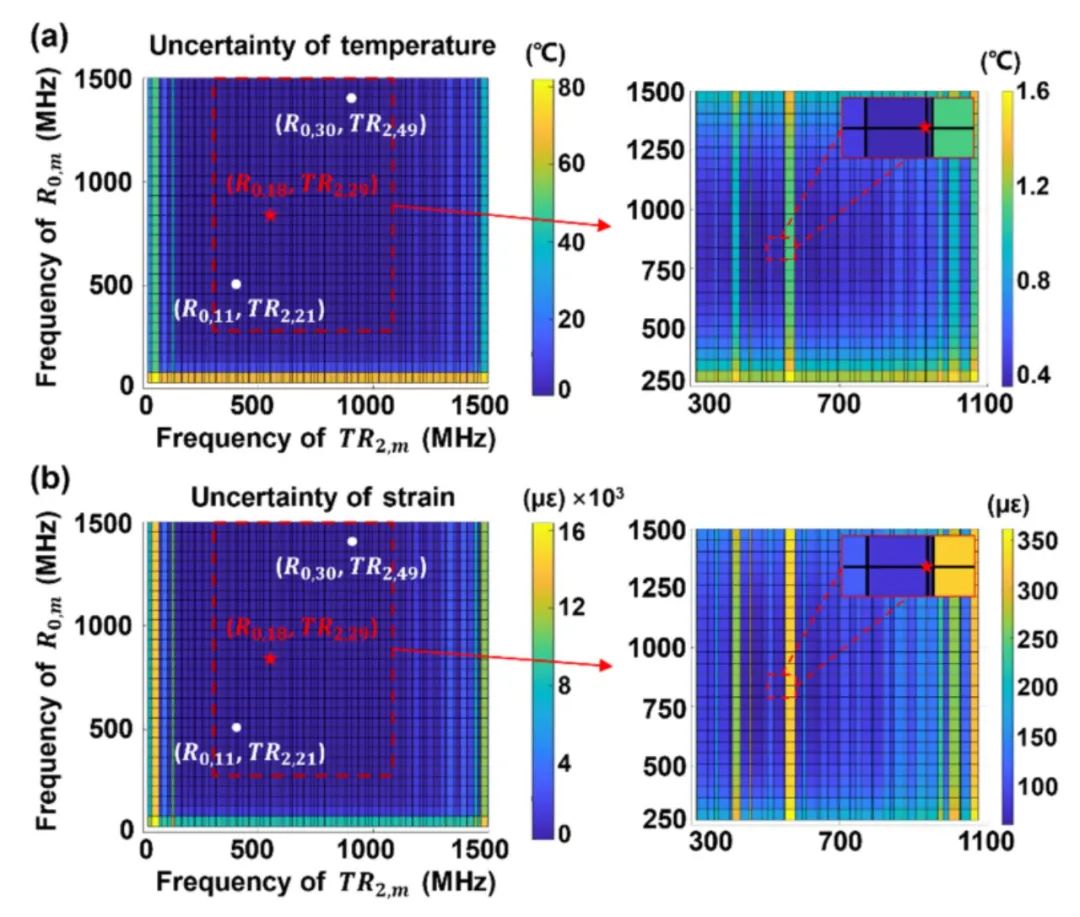
图9 不同模式组合的理论（a）温度和（b）应变误差。插图：虚线区域的放大视图

图源： Optics Letters （2023）。

https://doi.org/10.1364/OL.493637 （Fig. 2）

可以看出不同的模式组合会产生不同的测量误差，使用频率过高或过低的声学模式都会产生较大的误差。从图9中可以选出具有最小误差的模式组合（R0，18， TR2，29），理论误差为0.35°C/59.98µε。此外，还选择了（R0，11， TR2，21）和（R0，30， TR2，49）两种典型模式组合进行对比展示，其中前者具有高信噪比（理论温度/应变误差为0.48°C/80.33µε），后者具有高共振频率（理论温度/应变误差为0.9°C/174.22µε）。可见，同时使用高频声模或使用高信噪比都不能保证最佳精度，需要权衡信噪比和共振频率。

本工作使用了基于光纤萨格纳克环的实验装置，用于测量FBS频谱并展示基于HNLF中FBS的温度和应力同时传感。我们通过调整不同的温度和应力测量了六个模式在不同情况下的FBS谱。以图10为例，分别展示了R0，18和TR2，29模式在不同温度和应变下的频谱。之后绘制不同声模的共振频率与温度/应变的关系，如图11所示。我们可以看到R0，m和 TR2，m模式的共振频率与温度和应变呈线性关系，不同模式对温度和应变的灵敏度不同。我们计算了各个模式的温度及应力系数并在图11中进行了标注。

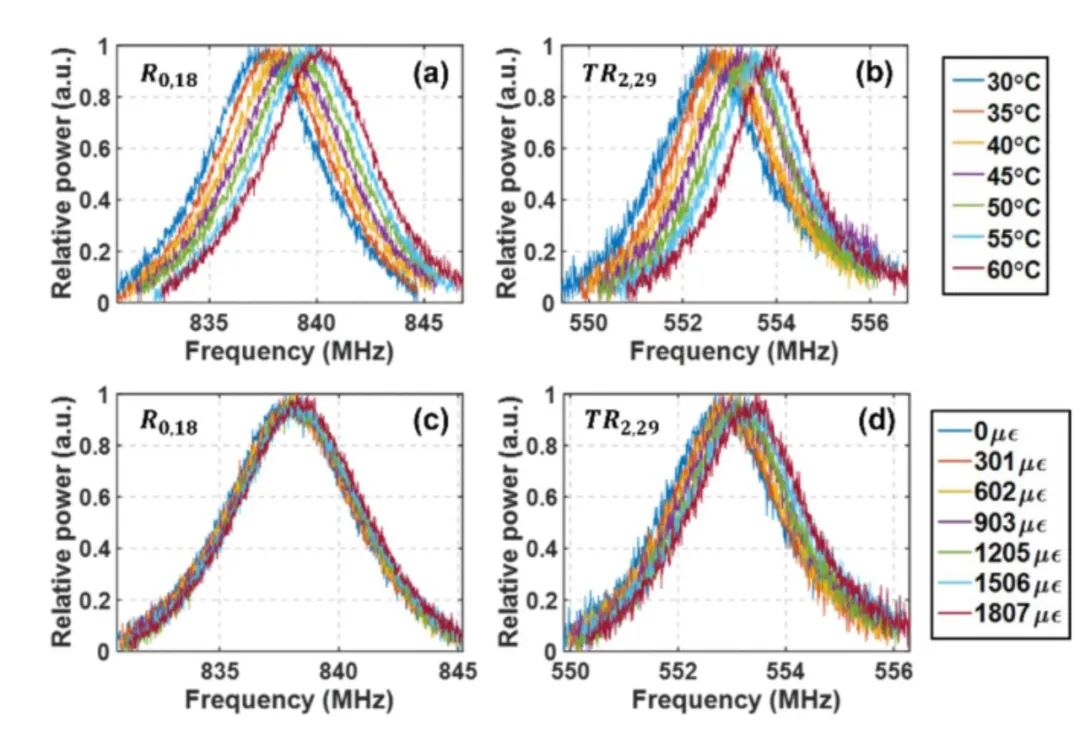
图10 （a， c） R0，18和（b， d） TR2，29在不同温度和应变值下的FBS频谱

图源： Optics Letters （2023）。

https://doi.org/10.1364/OL.493637 （Fig. 4）

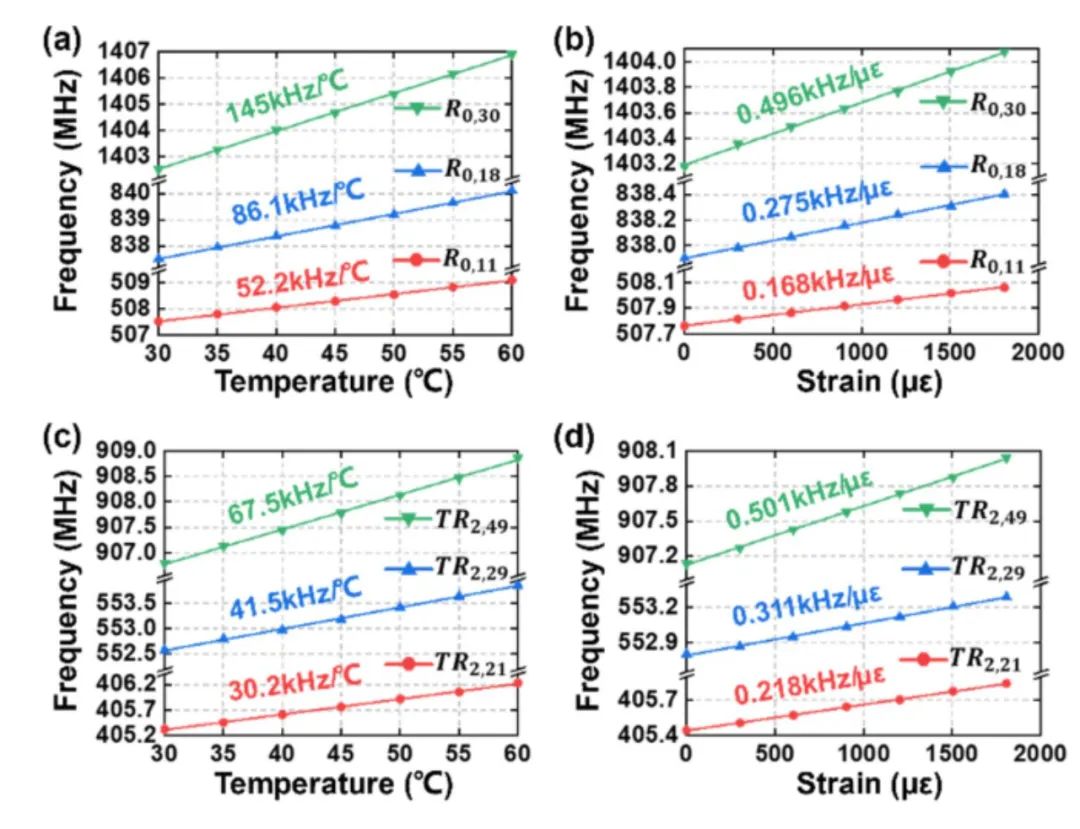
图11 （a， b） R0，11、R0，18和R0，30的共振频率与温度/应变的关系；

（c， d） TR2，21、TR2，29和TR2，49的共振频率与温度/应变的关系

图源： Optics Letters （2023）。

https://doi.org/10.1364/OL.493637 （Fig. 5）

最后在实验中设定三个具有不同温度和应力的状态，成功验证了该传感方法的有效性。结果如表1所示，表中给出了不同模式组合下的温度/应变测量误差（以标准差表示，标准差是通过重复测量10次获得的）。通过表1，可以得到使用（R0，18， TR2，29）的模态组合可以获得0.12°C/39µε的最低温度/应变误差，平均误差也仅为0.14°C/42.29µε。而使用另外两个模式组合所产生的测量误差则更大。实验结果再次证实，虽然（R0，11， TR2，21）模式具有高信噪比，但由于其相对较低的共振频率（或灵敏度），它们不能提供最佳精度。同样，（R0，30， TR2，49）模式组合虽然共振频率较高，但由于信噪比较低，仍然无法达到最佳精度。

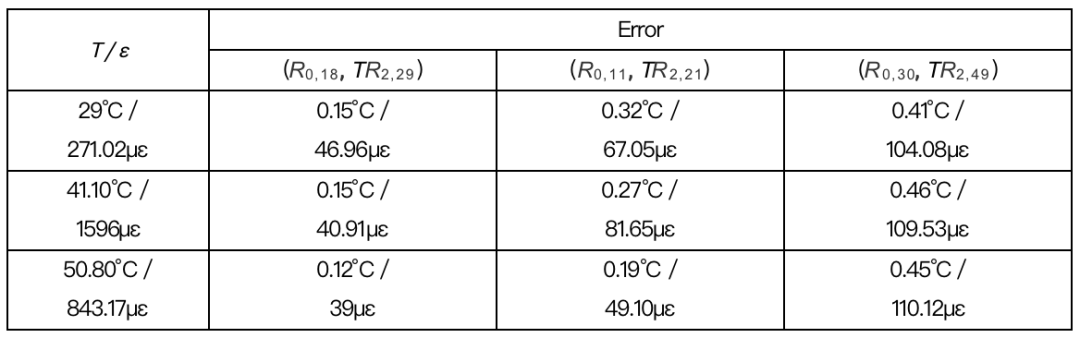
表 1实验测量误差

表源： Optics Letters （2023）。

https://doi.org/10.1364/OL.493637 （Table 3）

04 应用与展望

本团队提出了基于HNLF前向布里渊散射的高灵敏度声阻抗传感技术。利用HNLF中R0，m模式引起的前向布里渊散射，首次展示了超过3MHz/［kg/（s·mm2）］灵敏度的声阻抗传感。通过仿真分析，证明了HNLF中高阶声场模式的振动更密集且强度更集中在纤芯部位，因此相比于SSMF，HNLF具有更高的声光耦合效率及增益，从理论上展示了利用HNLF进行高灵敏度声阻抗传感的可行性。通过实验测量了HNLF和SSMF中的FBS增益谱，并利用其进行了声阻抗传感。结果表明，HNLF中R0，20模式的声阻抗灵敏度达到了3.83MHz/［kg/（s·mm2）］，而SSMF中增益几乎最大的R0，9模式的灵敏度仅为2.70MHz/［kg/（s·mm2）］，利用HNLF将声阻抗灵敏度提高了1.42倍。另外，本文也利用了HNLF中TR2，5模式进行声阻抗传感实验，测得其传感灵敏度为0.24MHz/［kg/（s·mm2）］，该数值比SSMF中相同的TR2，5模式的灵敏度高了1.5倍。

此外，本团队还成功地演示了基于HNLF中FBS的增强型温度和应变同时传感。通过使用具有较大FBS增益的高阶声模，提高了测量灵敏度和精度。之后为了解决信噪比和共振频率之间的权衡问题，提出了一种选择最佳模式组合以实现最小误差的方法，并通过仿真和实验进行了验证。当在HNLF中使用（R0，18， TR2，29）模式时，温度和应变误差最低为0.12°C/39µε。与基于BBS的传感器相比，该传感器只需要低频测量，不需要~10GHz的微波源，实现了较低的成本。同时，由于FBS频谱的共振频率和线宽较小，也进一步提高了测量精度。此外，如果结合时域分析技术，该方案也可以以分布式方式运行。相信基于FBS的传感方案将有潜力成为同时监测温度和应变的高精度且低成本的候选方案。