波特图稳定性判据为何存在严重的使用局限？

增益裕量GM>0，相位裕量PM>0

为何存在严重的使用局限，甚至直接失效。

典型奈奎斯特图→波特图稳定裕量

为了便于观察波特图的稳定裕量，以常见的：

• 0型（分母不含s），ω从0°出发（Re正轴），回到-270°（Im正轴）
• 1型（分母含s的一次方），ω从-90°出发（Im负轴），回到-270°（Im正轴）
• 2型（分母含s的二次方），ω从-180°出发（Re负轴），回到-270°（Im正轴）

系统为例，把三个系统的穿越频率ωc放在重合的位置，给出如下图示。

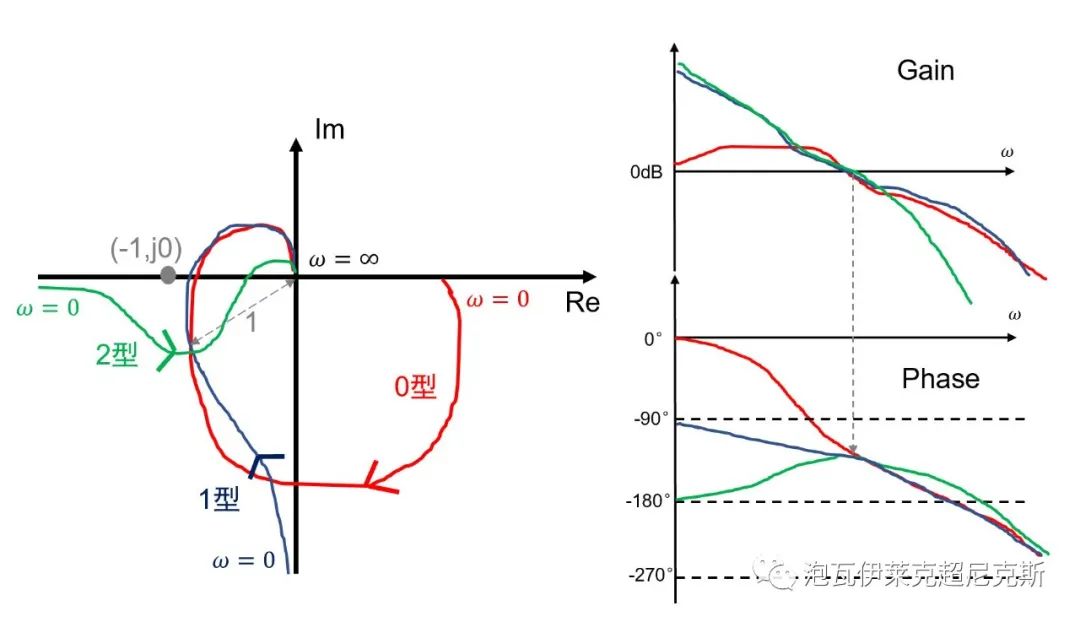
由图，三者的相位裕量PM≈45°相同，增益裕量GM则是绿色的2型系统大，红色0型和蓝色1型系统小。

• 结论：

典型形状的奈奎斯特图，对应到波特图时，稳定裕量GM/PM的物理意义是非常明确的，便于稳定裕量的定义，和稳定性判据的使用。

非典型系统→增益裕量无穷大

考察开环传递函数

G=s/(1+s)

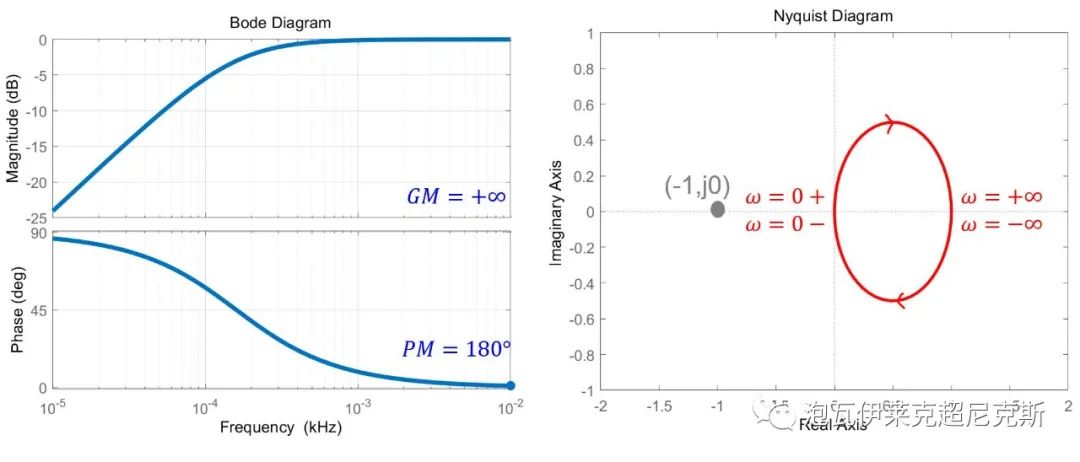
奈奎斯特图的增益无论如何增大，奈奎斯特图也不会包围(-1，j0)，故有GM=+∞；奈奎斯特图与Re正轴交点是(1，j0)，故有PM=180°。

再看波特图，与奈奎斯特图相对应，我们找不到幅频曲线与0dB交点，也找不到相频曲线与-180°交点。只能认为，频率无穷大处幅频与0dB相交，此时可以推出PM=180°；而相频永远不与-180°相交，所以GM=+∞。

考察开环传递函数

G=1/(s s (s+1))

这种系统是2型系统中的“结构不稳定”系统：若其分子增益和分母中一阶子系统的时间常数可调，无论如何调参，其闭环以后均不能稳定。

由奈奎斯特图可知，Z=N+P=1+0=1，闭环系统不稳定，且可以看出相位裕量PM为负，GM的话只有=-∞才有可能让极坐标图穿越(-1，0)。

再看波特图，PM为负是明确的；同时相频在频率为0处与-180°相交，故GM=-∞。

• 结论：

当相频不与-180°明显相交，仅从波特图观察稳定裕量GM并不十分直观。

局限1→幅频多次穿越0dB

考察开环传递函数

G=2*(s+0.05) (s+0.1)/(s (s+1)*(s+0.5))

波特图的幅频曲线，多次穿越0dB，给相位裕量PM的认定造成困扰。

由奈奎斯特图可知，Z=N+P=0+0=0，闭环系统稳定，增益裕量GM=+∞。

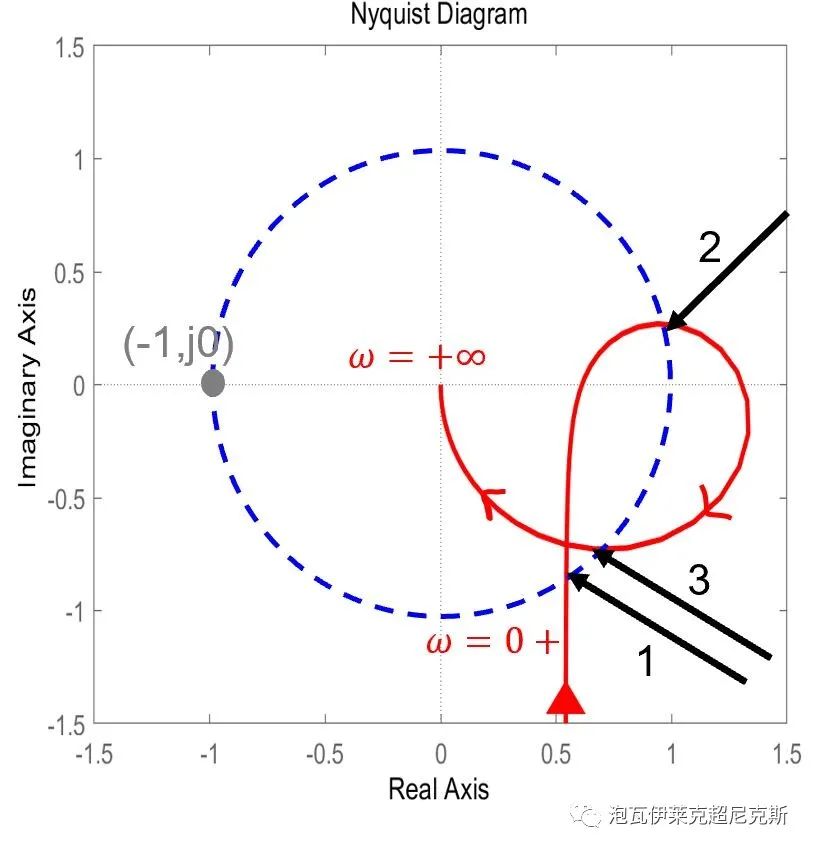
系统在频率1，频率2，频率3处依次穿越0dB线，当曲线顺时针旋转到频率1的位置与(-1,j0)相交后，系统已经开始不稳定。因此，相位裕量PM由频率1处（最小的穿越频率）的相角决定。

然而，倘若奈奎斯特曲线如下，当曲线顺时针旋转到频率3的位置与(-1,j0)相交后，系统已经开始不稳定。因此，相位裕量PM由频率3处（最大的穿越频率）的相角决定。

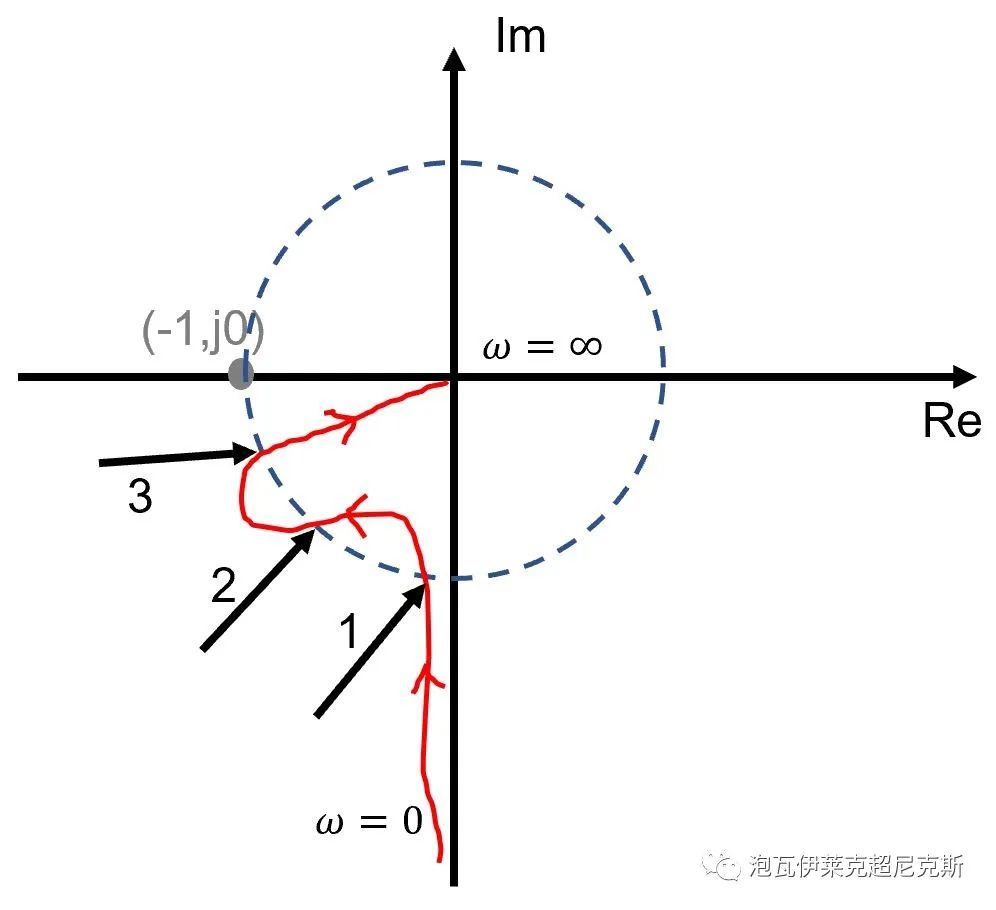
• 结论：

幅频多次穿越0dB，相位裕量PM可能由最小或者最大穿越频率处决定，取决于奈奎斯特图的具体形状。

局限2→相频多次穿越-180°

考察开环传递函数

G=15*(s+5)(s+15)/((ss+s+1) (s+0.5) (0.01*s+1))

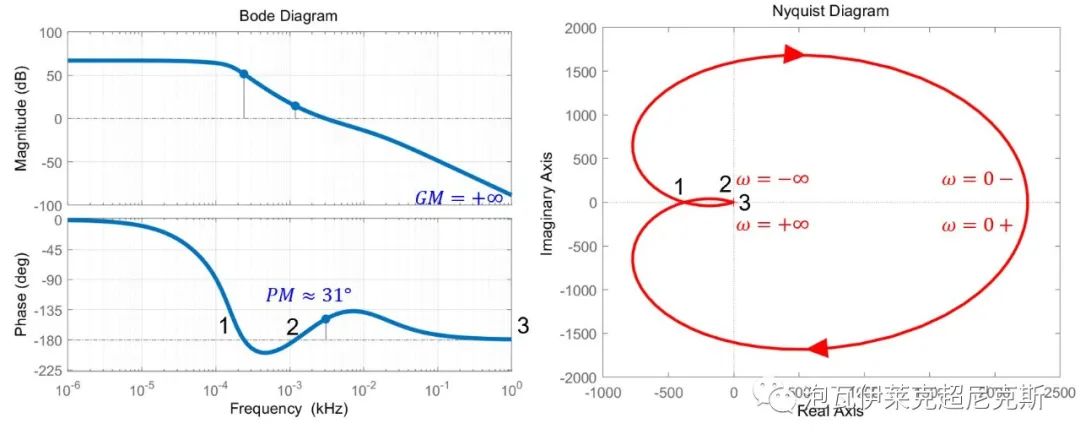
放大奈奎斯特图(-1,j0)附近穿越的细节，以观察频率2和频率3：

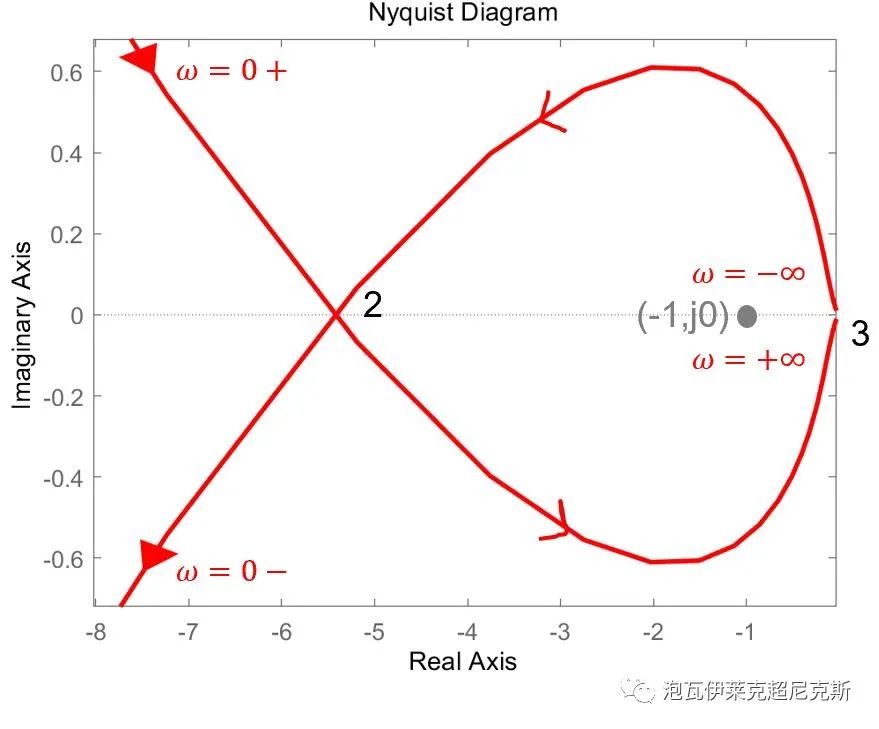
该例波特图中，相位裕度PM=31°是易见的，但相频曲线， 多次穿越-180°，给增益裕量GM的认定造成困扰 。

由该例的奈奎斯特图可知，Z=N+P=-1+1+0=0，闭环系统稳定，且应该得到增益裕量GM=+∞。

然而，上例只是特例，更普遍的，多次穿越-180°，形似该形状的奈奎斯特曲线可称作"条件稳定"系统。如下，(-1,j0)可能位于如下箭头指向的四个区间(1左侧，1-2，2-3，3-4)。

若(-1,j0)在频率1左侧，则存在若干的不连续增益区间，使系统稳定。这样一来，增益裕量GM是无法定义的：不存在一个GM，使得系统增益超过它后就不稳定，因为一个更大的增益区间会使系统又重新稳定。

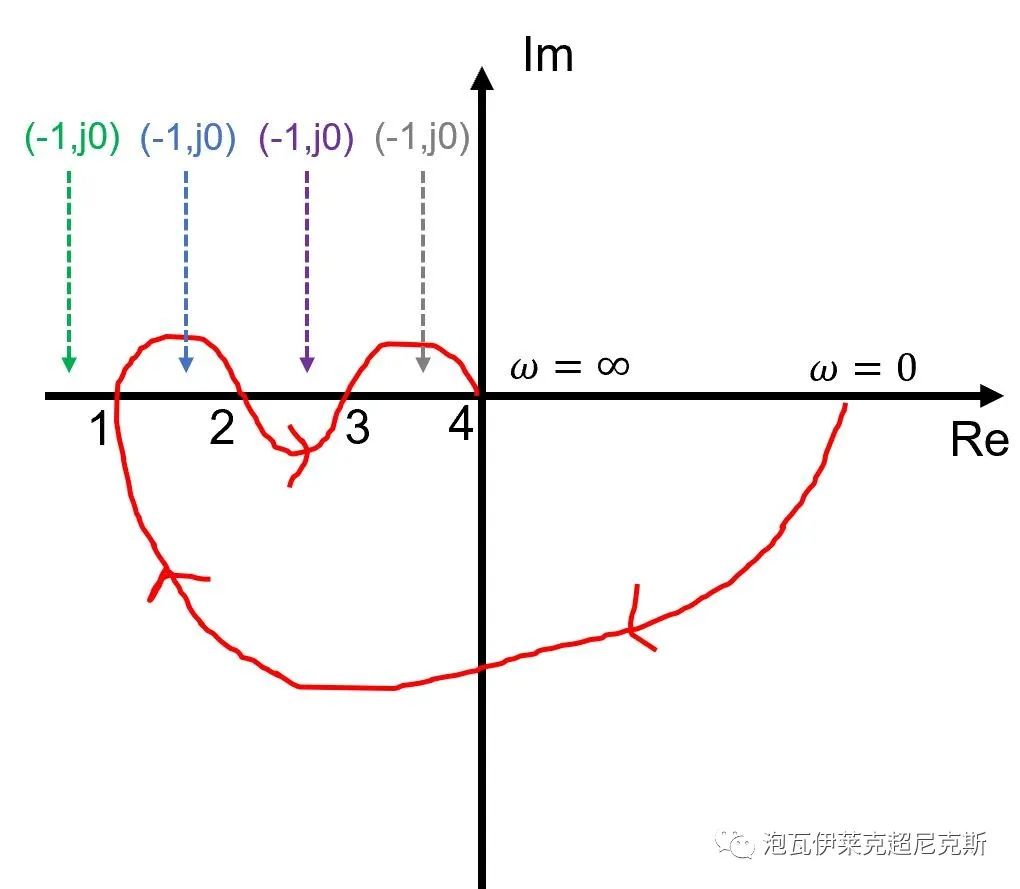
• 结论：

幅频多次穿越-180°，若是“条件稳定”系统，增益裕量GM无法定义，失去物理意义。

失效→增益裕量GM<0才稳定

考察开环传递函数（非最小相位）

G=5*(s+3)/(s*(s-1))

由波特图，**增益裕量GM=-14dB<0， **相位裕度PM=51.6°>0，根据判据，判为闭环不稳定系统吗？

再看奈奎斯特图，由于开环函数G含有一个右半平面不稳定极点，即P=1，那么Z=N+P=-1+1=0，闭环系统稳定！

• 结论：

存在开环不稳定的非最小相位系统，其波特图稳定裕量判据是：增益裕量GM<0，相位裕量PM>0。

总结

基于波特图的稳定裕量和稳定性判据，仅仅是针对典型系统的“工程性”简化方法。

奈奎斯特图才是判断系统绝对稳定性和相对稳定性的有效频域工具。

*注： 奈奎斯特稳定性判据在不同资料中形式不尽相同，本文采用的定义如下。

Z为闭环系统不稳定的极点个数，Z=0代表闭环系统稳定； P为开环函数不稳定极点数，N为完整正负频域的闭合奈奎斯特曲线包围(-1,j0)的带符号圈数总和，顺时针计为+，逆时针计为-。