

什么是空间矢量呢?为啥不能将电流看作空间矢量呢?
电子说
描述
1,空间矢量
什么是空间矢量呢?
定义:在电机内,可将在空间按正弦分布的量表示为空间矢量。
1.1定子磁动势空间矢量
啥叫磁动势?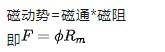
我们知道磁通是有方向的,那么磁动势当然也是有方向的。这应该没毛病吧。
那么定子产生的磁场方向如何呢?
如下图,给绕组通电,根据右手定则 会产生如图所示磁场。
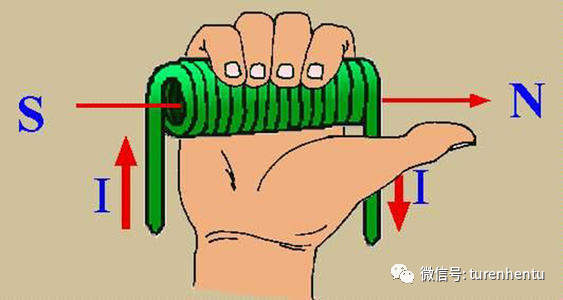
Fig 1 电流产生磁场
推而广之,如下图:
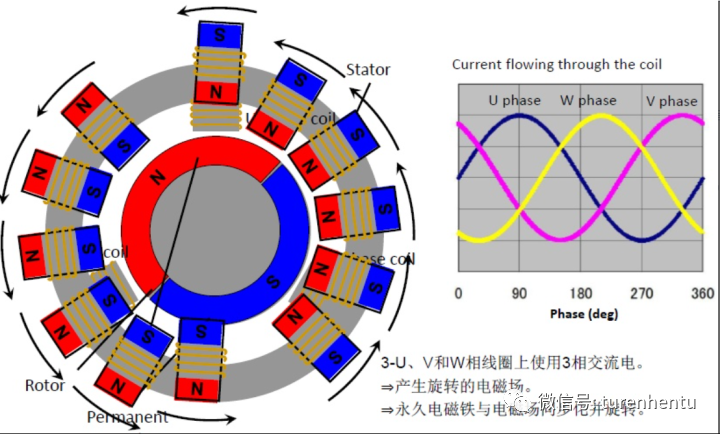
Fig2 电流产生磁场(盗用一张图,如有侵权,请联系我删除)
由Fig2可知,可将通入交变电流的定子绕组等效为一个个小磁铁。这些磁铁的磁场方向当然是非常明确的,那么在某个瞬间其合成磁场也应该是明确的。按一定顺序使定子绕组导通,便产生了沿圆周方向不断运动的定子合成磁场,从而拖动永磁体转子沿一个方向不断运动(异性相吸原理)。
当我们按照上图这样想的时候,其实磁动势空间矢量的概念呼之欲出啊。而磁动势为什么沿空间正弦分布呢?可以简单地归结为,和电机设计内容相关(比如定子绕组的分布方式等)。
所有绕组,最终可以简化为,位于a,b,c三相轴线上的三个线圈,通入电流后,会产生与实际相绕组等同的磁动势。如下图,图中ia/ib/ic为各相电流的正方向。
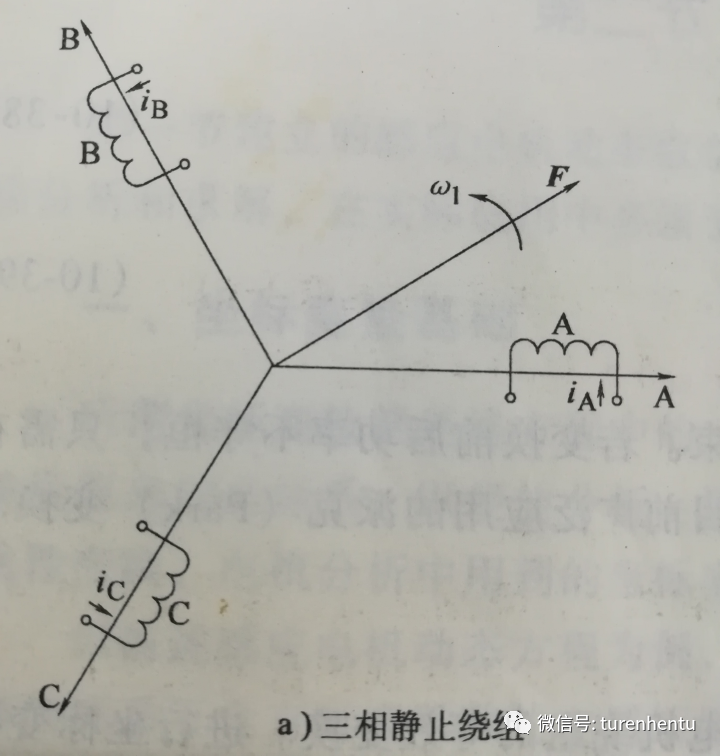
Fig3 等效绕组形式
可知,a/b/c三相各自产生的磁动势空间矢量和各相轴线方向平行(根据电流方向取与轴线方向相同或者相反)。
为了助于理解,放一张磁链空间矢量动图:
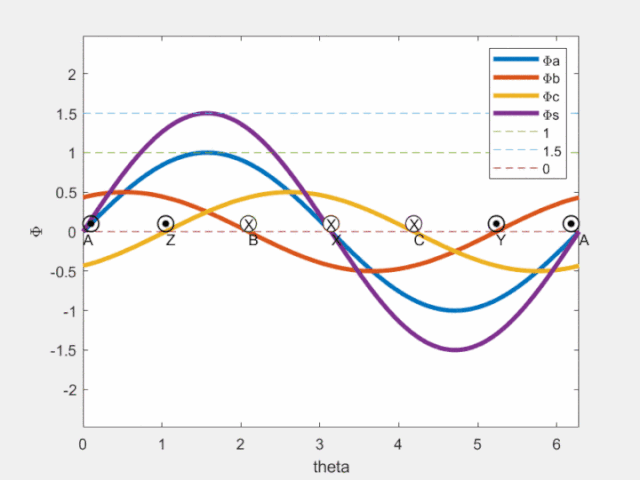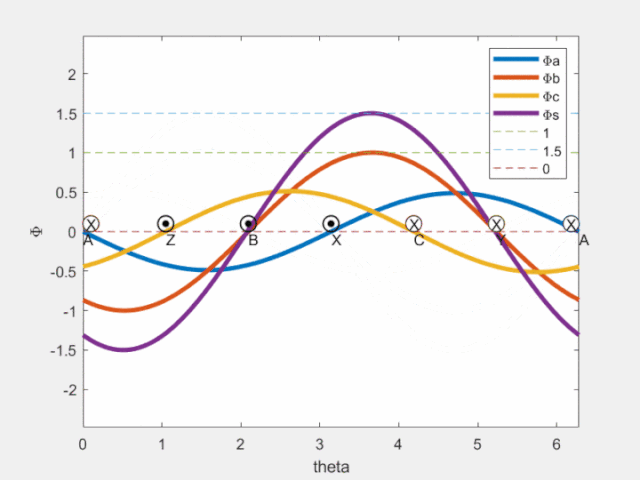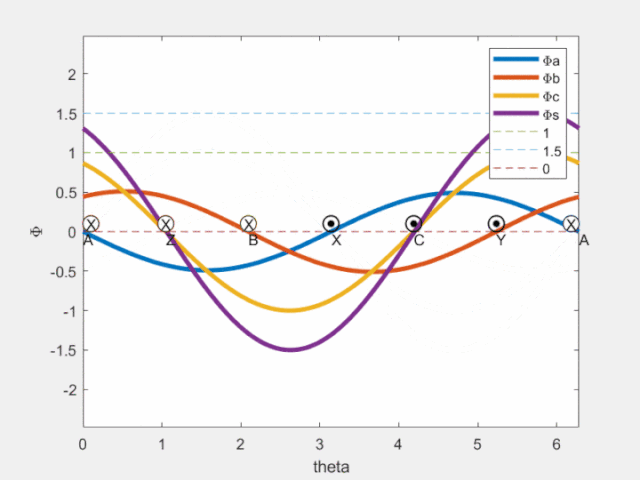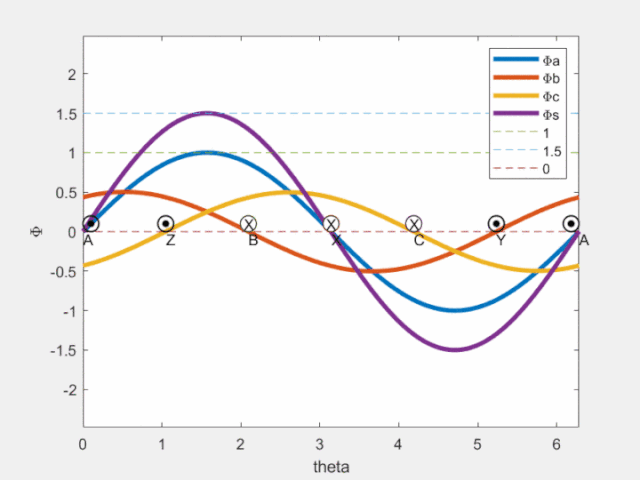
Fig4 磁链空间矢量
由上图可见,a/b/c各相产生的磁链在该相轴线处脉动;图中紫色曲线为合成磁链空间矢量,可知其在空间按正弦分布,且沿圆周旋转(旋转磁场,转一周,即可获得理想磁链圆)。
是不是证明了这么一句话:在电机气隙内,定子磁场按正弦分布。
1.2 电流空间矢量

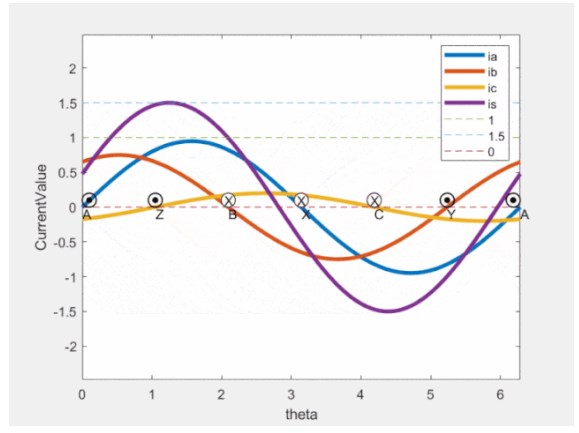
Fig 5 电流空间矢量
其中:
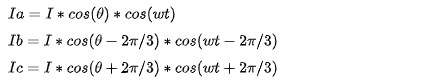
上述公式组中的第二个cos很好理解,表征通入的三相正弦电流,大小随时间变化;上述公式组中的第一个cos,可能会让新手有点蒙圈。前面提到了,其实这个cos的根源和定子绕组的处理方式有关(分布绕组/短距绕组可以让绕组合成磁动势更加接近正弦)。
从图上可见,a/b/c三相电流在空间按正弦分布,且在轴线方向来回脉振,但其合成电流空间矢量Is却绕圆周不断旋转。
如果将上图中电流乘以K再除以磁阻呢?就得到Fig 4 中磁链空间矢量。
电流空间矢量概念存在的前提是,必须将之和磁动势空间矢量建立联系。
即电流空间矢量的理解需要依托于磁动势空间矢量,两者之间只差一个系数,方向相同。
你将磁动势作为空间矢量,为啥不能将电流看作空间矢量呢?
1.3 电压空间矢量
如果说电流空间矢量尚有迹可循,那么电压空间矢量真的似无源之水!
其实,仍旧规定,各相 电压空间矢量方向与绕组轴线方向平行 。
还记得大明湖畔的夏雨荷吗? 啊不,还记得理想磁链圆不?
既然是磁链圆,说明磁场方向会发生变化。什么导致磁链改变方向呢?因为电压的作用啊。
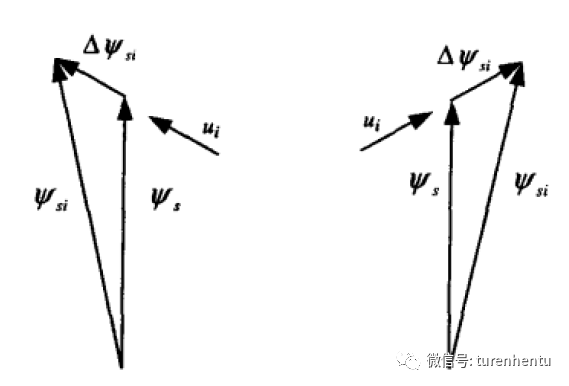
Fig 6 电压积分改变磁链方向
对于定子绕组来说,满足:

即,电压积分导致磁链变化。
如下图,合成电压空间矢量超前合成磁动势空间矢量90度,拉着磁链沿磁链圆运动。那么控制产生理想磁链圆的关键就是选择合适的电压空间矢量了。
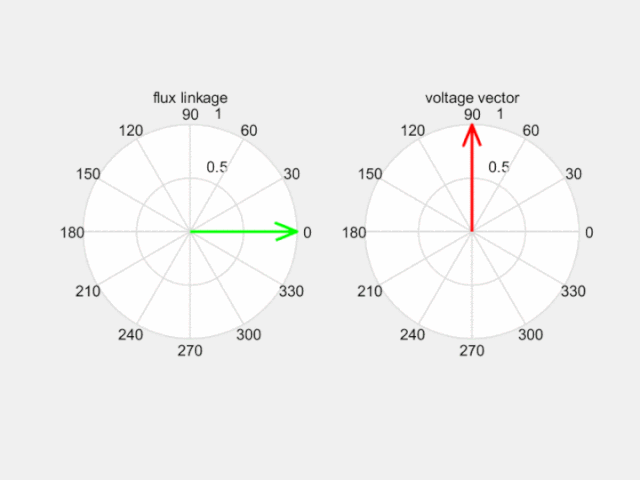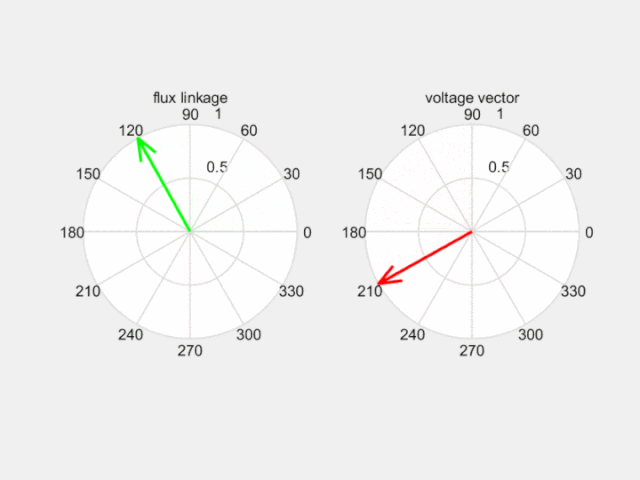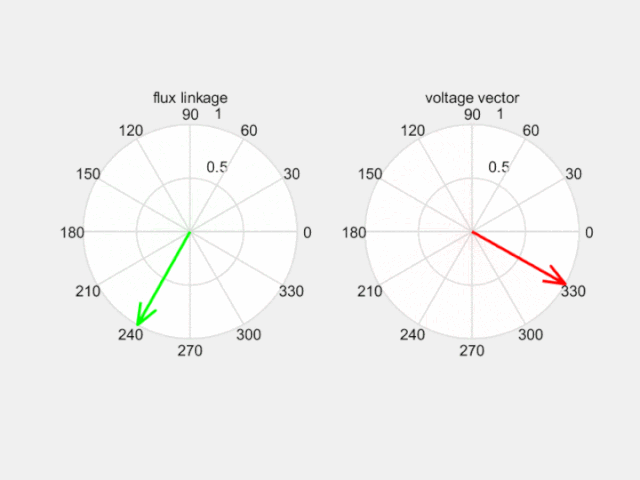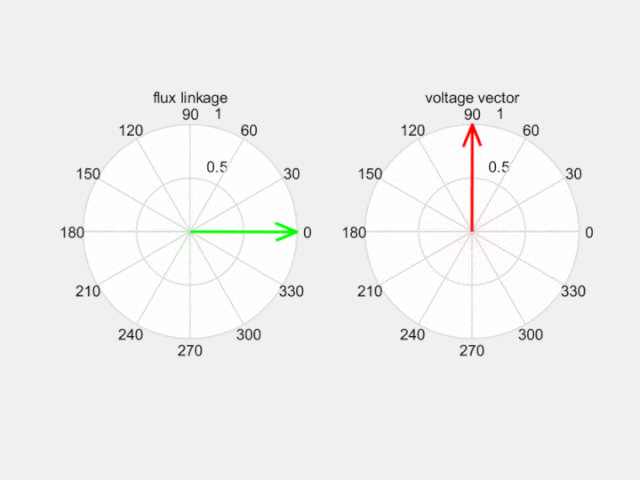
Fig 7 电压空间矢量改变磁链空间矢量
那么好了,前面定义说,三相电流空间矢量/三相磁动势空间矢量/三相电压空间矢量均位于绕组轴线方向(或者相反方向),你上面又说合成电压空间矢量相位超前磁链90度(理想情况下)。这该如何理解呢?
由于电压和电流本身存在时间上的相位差(理想情况,忽略电阻,电压相位超前电流相位90度,而电流和磁动势同相位),导致合成电压空间矢量与合成磁动势空间矢量在空间上存在相位差。
如下动图:
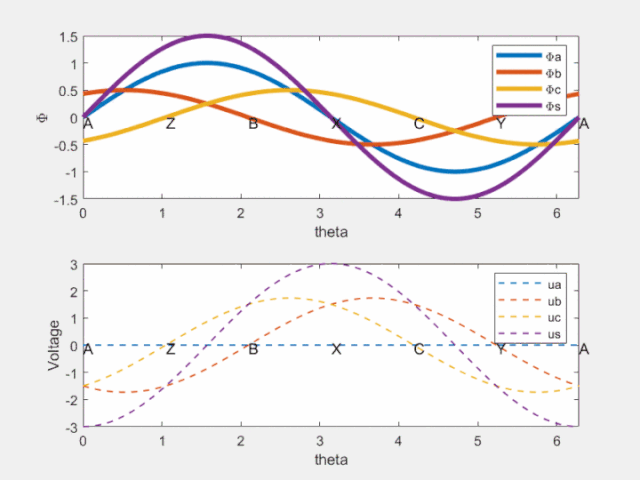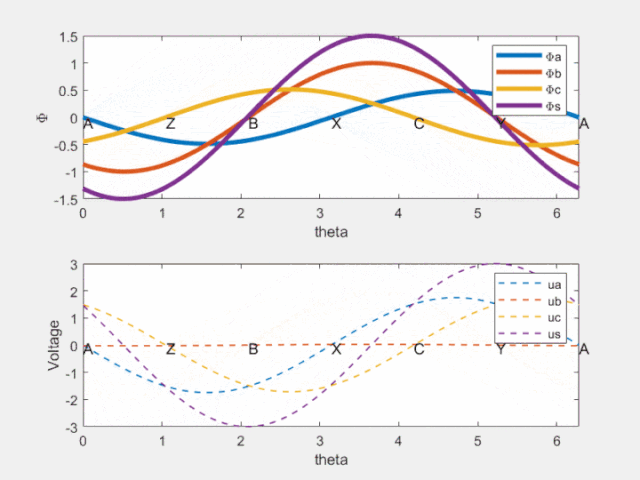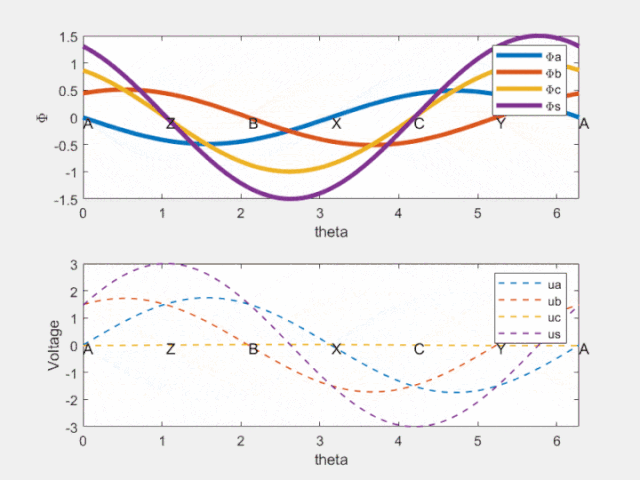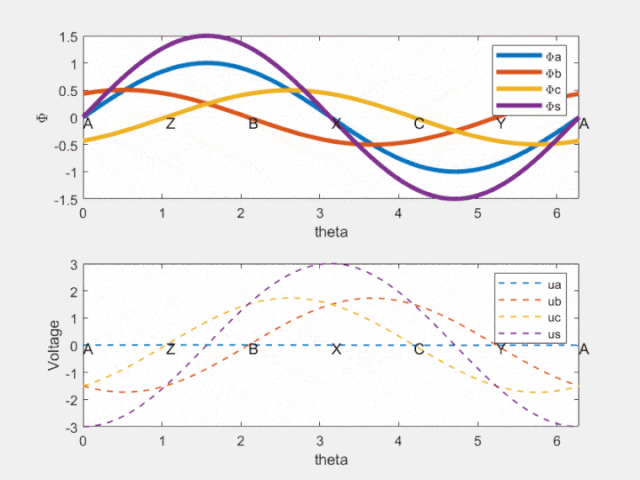
Fig 8 时间相位差反映在空间相位差
由上图可知,紫色的虚线相位超前紫色的实线!这就是电机旋转的原因啊
电压空间矢量存在的前提是,仍旧需要将其和磁动势空间矢量概念联系起来。

推理过程见下图:

Fig 9 空间矢量电压公式推导
于是,你发现Uout的幅值是Ua/Ub/Uc三相电压幅值的1.5倍。
那么空间矢量Uout在a/b/c 三轴线上的投影为多少呢?
你会发现:

而三相相电压合成矢量如何表示呢?
如下图,三相相电压合成电压矢量的所有情况均被限制在正六边形内部,即从正六边形中心O点出发,终点落在正六边形边界上的一系列矢量(图中只画出了第一个扇区的部分矢量)。
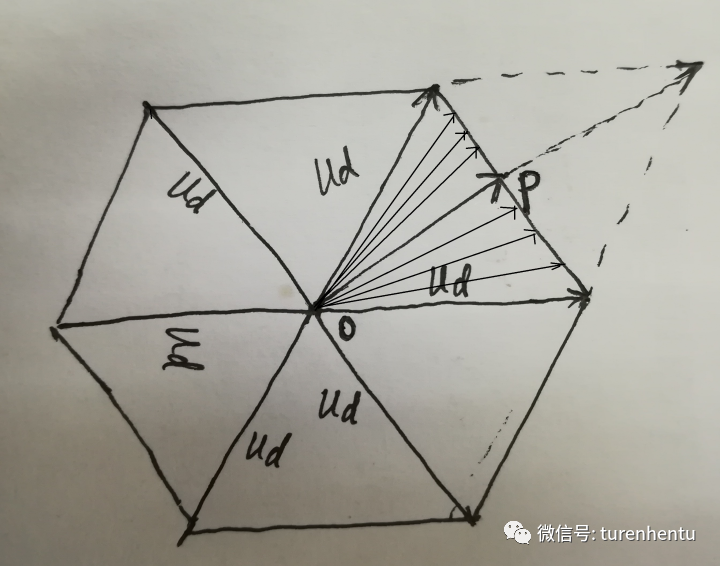
Fig 11 合成空间矢量
为什么最大的矢量是Udc呢?
我们知道,6个功率开关可以由8个最基本的电压矢量组合,其中6个非零的电压矢量组合即对应图中的6个Udc。
以a相上管导通,b,c相下管导通为例,如下图:
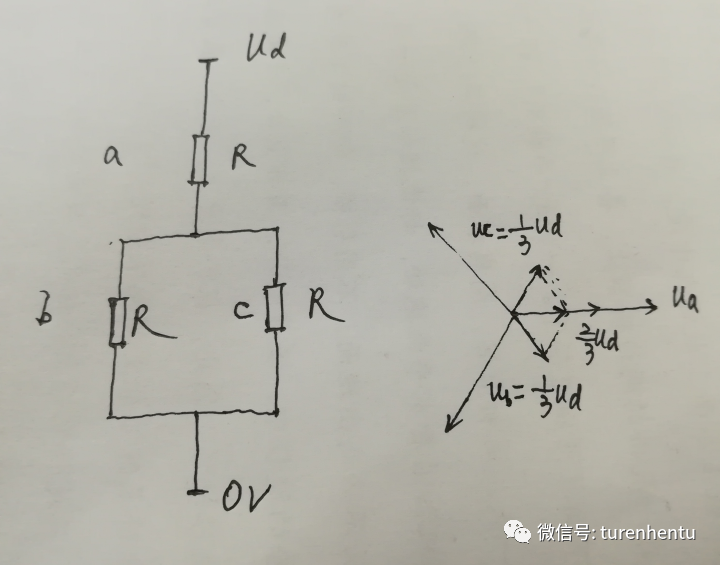
Fig 12 电压合成矢量
此时合成的空间矢量大小为Ud。最大也只能这么大了。不信你可以试试看~
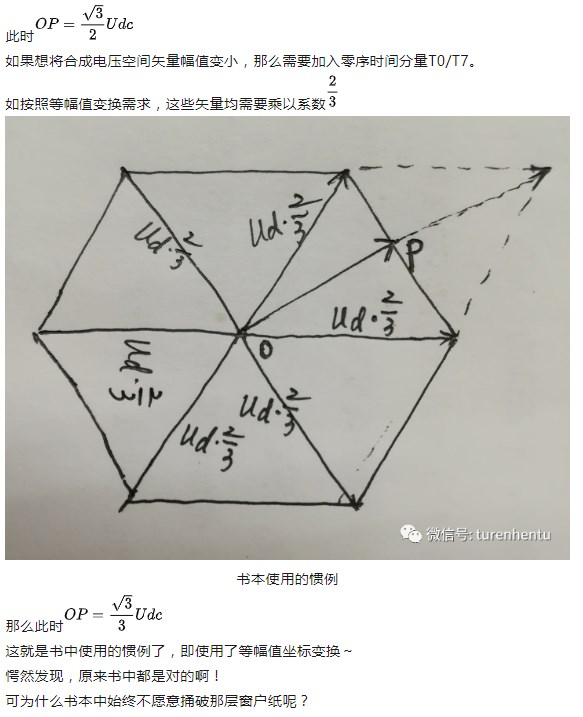
那么在P点处,三相合成电压矢量大小还能到Ud吗?
当然不能,前面已经说了不能超过正六边形边界,不管你用什么过调制方法啊,合成矢量均位于正六边形内部。(注意,这里说的三相合成电压矢量利用了等效的概念,即伏秒原理,如果不这样想,那么某个瞬间,电压矢量只能是8个基本矢量的一种情况了)。
此时应该由相邻的两个电压矢量(比如U1和U2)进行等效合成。假设U1作用时间为T1,U2作用时间为T2,那么P点处,必定满足T1+T2=Ts(Ts为时间步长),当P位于边长中点处时,T1=T2=0.5*Ts,不要问我怎么证明了哈,我已经在图中画出来了。
-
电压空间矢量与磁链矢量的关系是什么2024-10-12 3010
-
空间矢量调制技术(SVPWM)2023-05-29 6526
-
空间电压矢量调制SVPWM技术详解2021-11-22 1021
-
空间矢量调制的介绍和基本原理资料概述2018-11-07 3456
-
空间矢量脉宽调制技术2018-10-29 1682
-
空间矢量控制(SVPWM)原理2016-03-30 785
-
基于DSP的空间电压矢量法PWM的研究_王妍2016-01-08 537
-
基于DSP的空间矢量脉宽调制(SVPWM)的实现2010-03-01 587
-
空间矢量PWM逆变器死区效应分析与补偿方法2010-02-22 792
-
电压空间矢量研究及Matlab仿真2009-12-21 3239
-
整流器空间矢量调制算法的比较研究2009-07-08 1673
全部0条评论

快来发表一下你的评论吧 !

