LinearAmplitude滤波器设计详解

本文提出了一种新型的滤波器，其频响具有直线特性，本文将详细解释如何推导这种特殊的滤波器。最后介绍基于Matlab的滤波器设计软件，以低通为例，展示其功能。给出Github相关链接。

直线幅度滤波器特点和用途

直线幅度滤波器(Linear Amplitude Filter, LR Filter)滤波器本公众号首次公开的一种滤波器，其幅频特性在某一点上具有最佳直线幅度逼近特性，这种滤波器可以用于补偿线缆插损，可以用于幅度均衡和滤波器两用。

直线幅度滤波器

直线幅度滤波器是一类特殊的理想滤波器，其地位和矩形滤波器以及高斯滤波器相当，是无法通过多项式直接拟合得到的，只能通过函数逼近的方式得到，现在我们总结下现有滤波器设计。

总共有三类滤波器综合如下(当然这个图还可以扩展)：

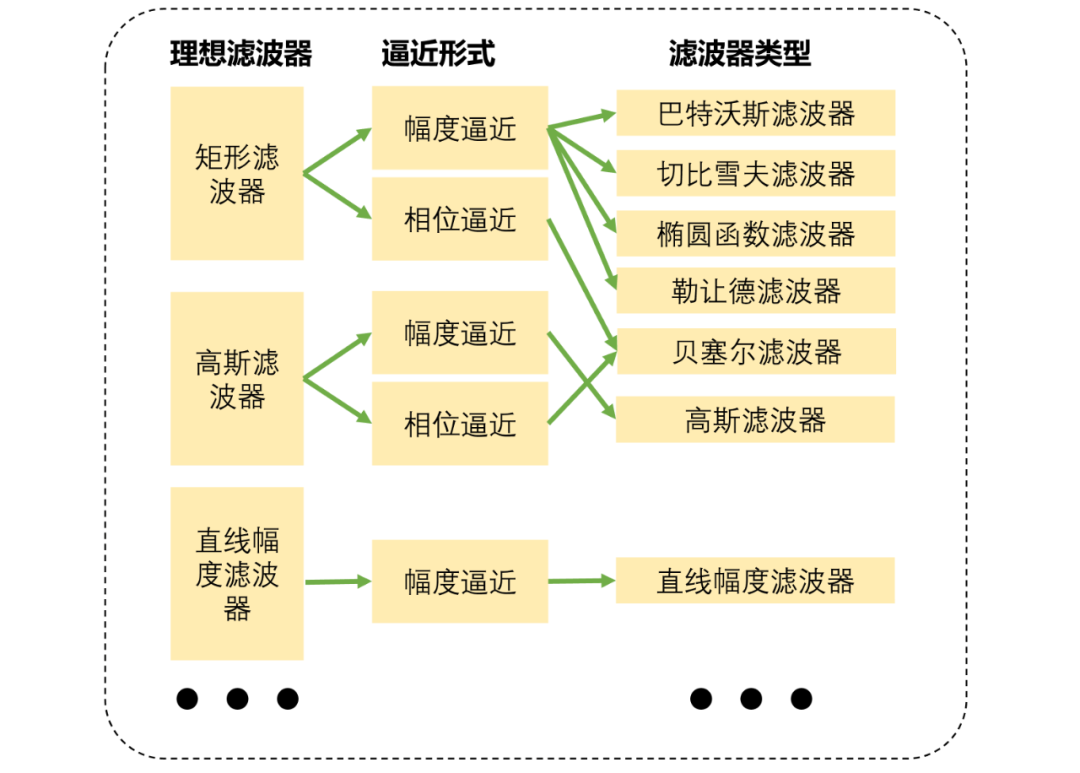
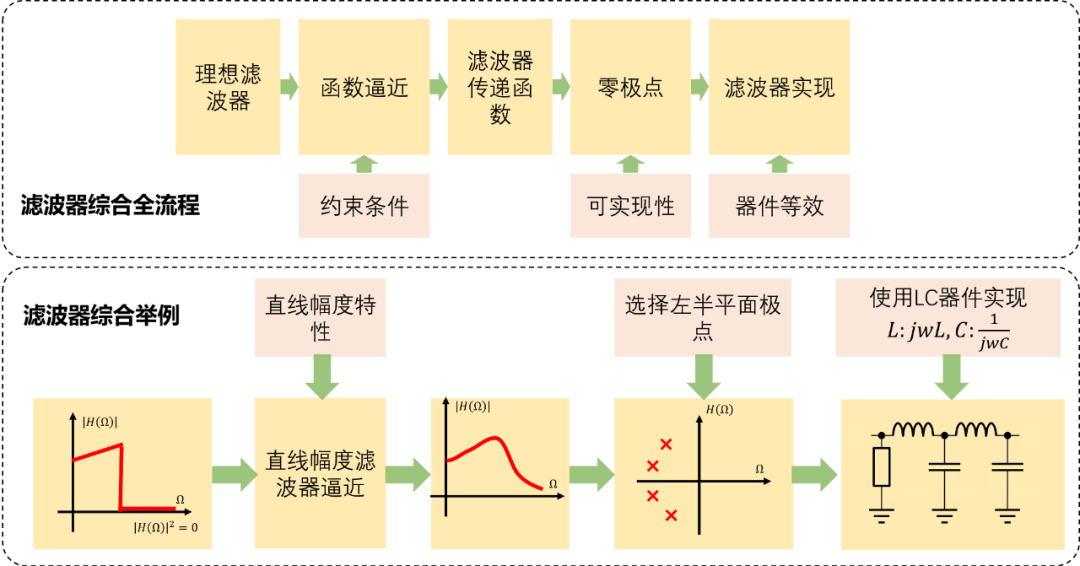
直线幅度滤波器综合全流程如下：

直线幅度滤波器逼近

这里定义直线幅度滤波器的幅频响应为：

其中为阶直线幅度滤波器多项式。

约束

1, 是阶多项式(可实现性，在频率增益为0)

2, (直线特性第一点，在频率为0的位置增益为，其中)

3, (直线特性第二点，在频率为1的位置增益为)

4, (直线滤波器带宽定义，幅度最高点规定为1)

5, 在通带范围内逼近直线(直线幅度滤波器特征)

直线幅度逼近

首先需要澄清一点是定义，为了可实现性，因为只有多项式是偶次项才能实现，偶次就意味着零点关于虚轴对称，所以，最后滤波器极点就一定可以选择到左半边平面，是可以实现的。

照例我们定义:

是一个偶次多项式。

由约束2和3可以绘制出理想滤波器草图：

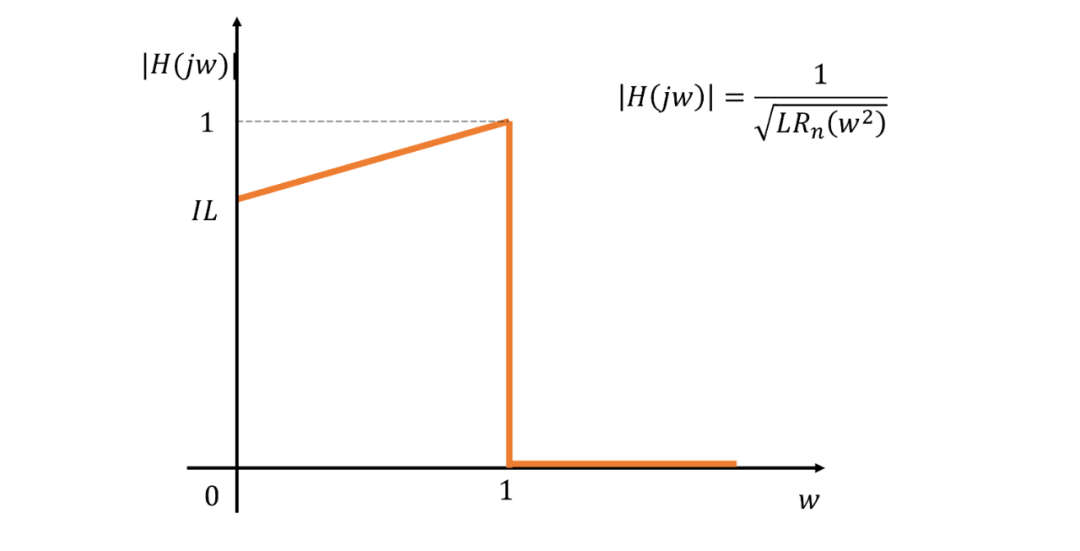
那么我们可以得到直线滤波器在带宽范围内的直线表达式：

由约束1，是一个多项式，所以在区间范围内，结合式和式，得到：

变量代换得到：

我们得到了理想滤波器在范围内的函数关系式，这里使用泰勒展开来进行幅度逼近，其中展开的点可以在范围内随意指定:

为简单起见，这里将展开点定为，并且，使用wolfram alpha计算：

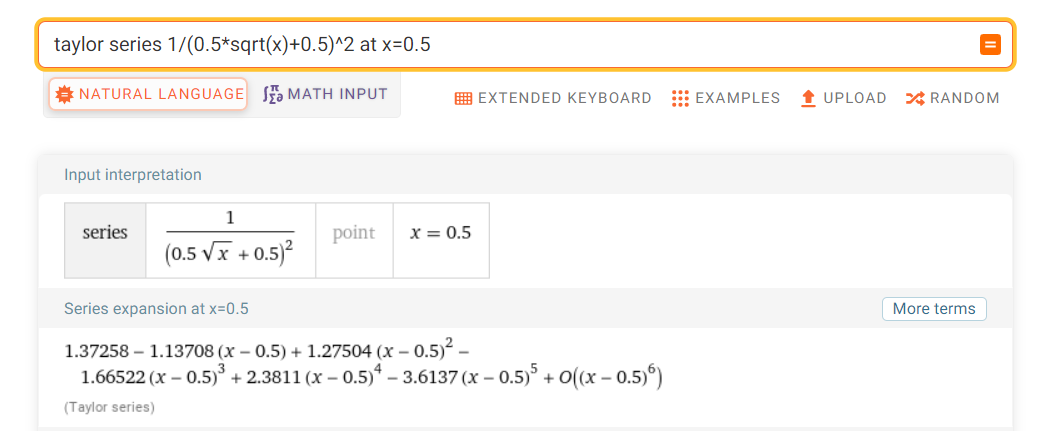
得到：

从泰勒逼近式我们可以看到，只能取偶数，当为奇数时，最高次项是负，当频率为无穷时，，违反约束1。这里取，得到:

看看逼近效果：

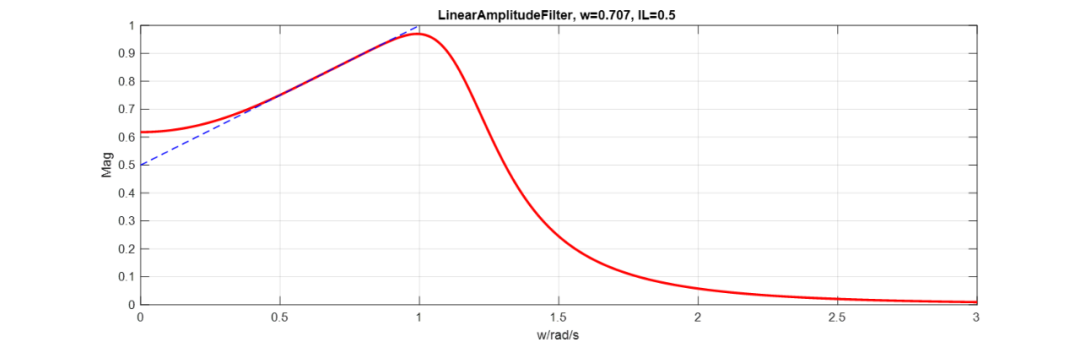
由于泰勒逼近只在有效，所以最终逼近后约束2,3,4将失效，所以需要对式和进行处理，由约束3,4以及式可以得到多项式：

所以需要调整直线的截距来达到约束条件：

要依据式(8)和泰勒逼近(6)联合得到所需的和展开点，最终求解的方程为：

两个方程两个未知数，式(8b)求解过程非常复杂，我们采用数值求解方案：这里采用了chebfun函数逼近库来计算，得到时,, ，多项式为：

最终效果如下：

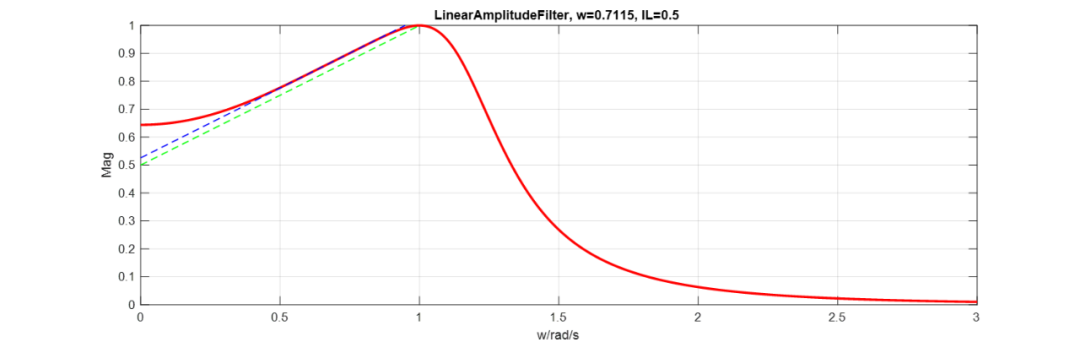
这个滤波器就是带宽为1，斜率为0.5的4阶直线幅度滤波器响应。

那么当阶数增加，逼近效果怎样呢，这里制作了阶数从2到20阶的幅度响应动图(图中对比了Butterworth频响)：

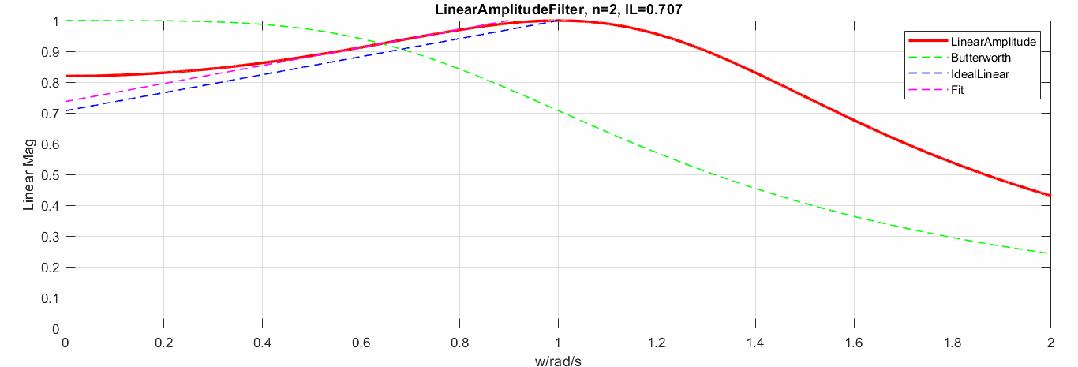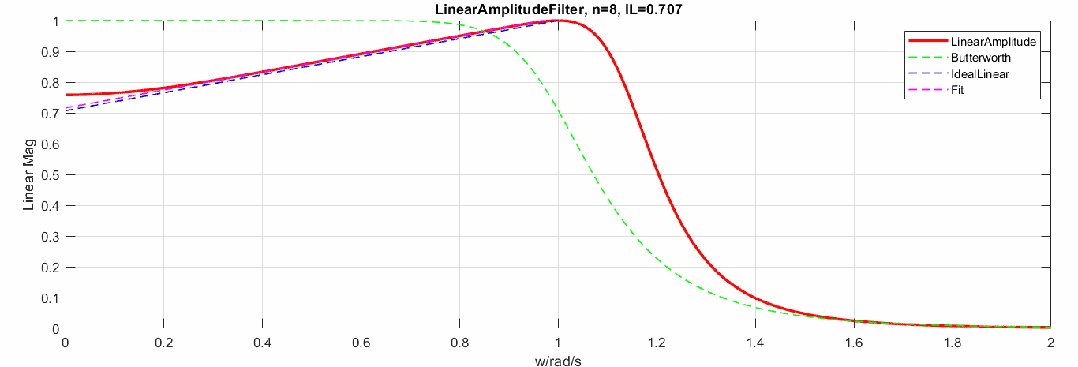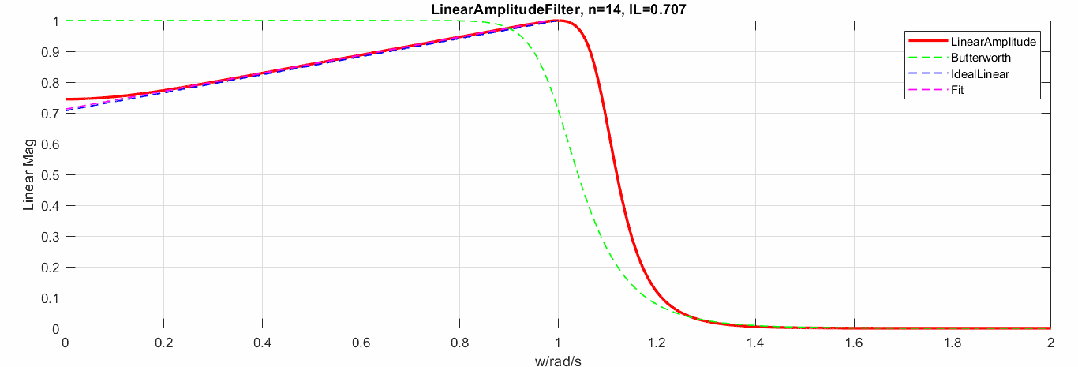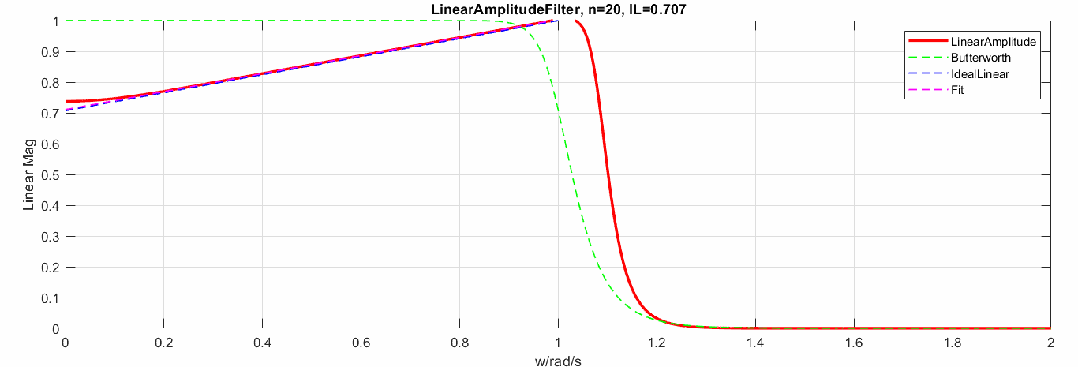
下图是将幅度修改为dB，频率轴还是线性：

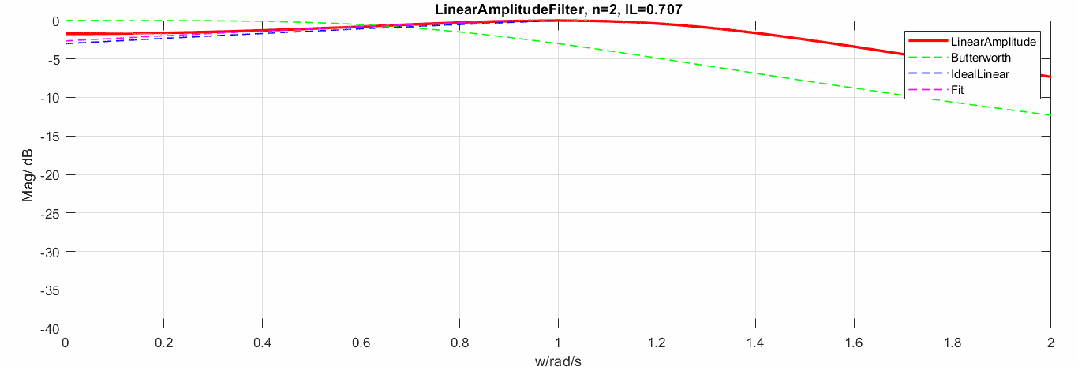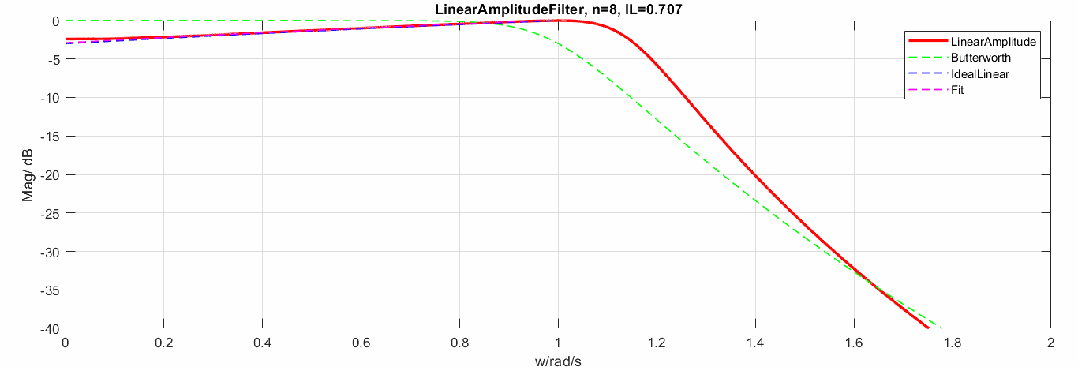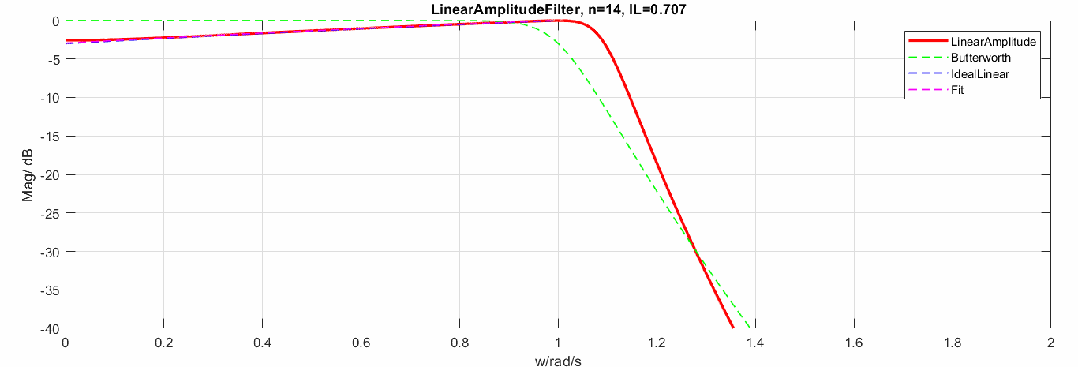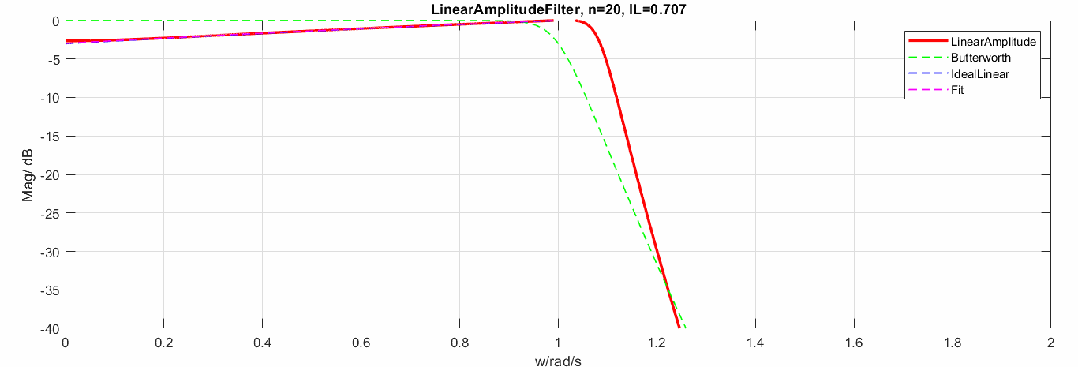
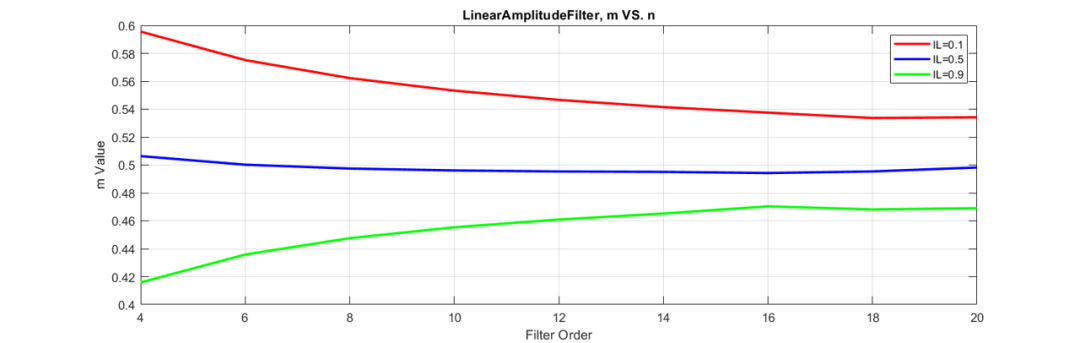
归一化参数与阶数的关系如下，当阶数升高，最终值会趋于0.5。图中16阶后曲线有偏移是因为计算精度问题。

奇数阶滤波器设计

目前还未找到一个有效的办法解决奇数阶直线幅度滤波器的设计(探索了几个方案均不满意)。

线性幅度滤波器多项式

和勒让德滤波器类似，线性幅度滤波器多项式并没有统一的公式来求解，这里采用了Matlab的符号计算工具来进行求解：

 

%--------------------------------------------------------------------------
% Edited by bbl
% Date: 2023-07-03(yyyy-mm-dd)
% 线性幅度滤波器系数设计
% 注意返回值低次在前，高次在后
%--------------------------------------------------------------------------
function [Ln] = funGenLinearAmpPoly(FilterOrder, IL)
if mod(FilterOrder, 2)
    Ln = [];
    warning('FilerOrder must be even');
    return;
end
% 使用chebfun函数计算m和b，使得在w=1处有单位增益和最大值
[m, b] = funLinearAmpGet_mb_chebfun(IL, FilterOrder);
if FilterOrder > 20
    dig = 100;
else
    dig = 16;
end
syms x
% 定义了直线幅度滤波器传递函数
f = 1/((1-IL)*sqrt(x)+b)^2;
a = sym(m);
coeffsx = sym(0);
for k = 0:FilterOrder
    kk = sym(k);
    % 使用在x=m处的麦克劳林展开得到系数
    coeffsx = coeffsx + vpa(subs(diff(f, x, kk) / factorial(k), x, a)*vpa((x-a)^kk, dig), dig);
end
polyx = coeffs(coeffsx);
% 计算平方的系数
Ln = vpa(zeros(1, length(polyx)*2-1), dig);
Ln(1:2:end) = polyx;
end

 

输入，的到参数：

 

>> [Ln] = funGenLinearAmpPoly(2, 0.707)
Ln =
[1.4882, 0, -0.9764, 0, 0.4882]

 

也即得到2阶直线幅度滤波器多项式：

这里给出数值计算出的线性幅度滤波器前14阶偶数滤波器多项式(注意这里不是特征多项式)：

滤波器阶数
2
4
6
8
10
12
14

在s平面取其左半边极点得到前14阶偶数线性幅度滤波器系数为(时幅度为1，时幅度为0.707)：

滤波器阶数
2
4
6
8
10
12
14

前14阶线性幅度滤波器极点为(时幅度为1，时幅度为0.707)：

滤波器阶数
2
4
6
8
10
12
14

线性幅度滤波器零极点

不同参数对线性幅度滤波器的极点影响如下图所示，其极点分布推测和高斯滤波器一样符合某种Szegő曲线分布(其中两个参数为0.5，另外一个参数从0.1扫描到0.9)：

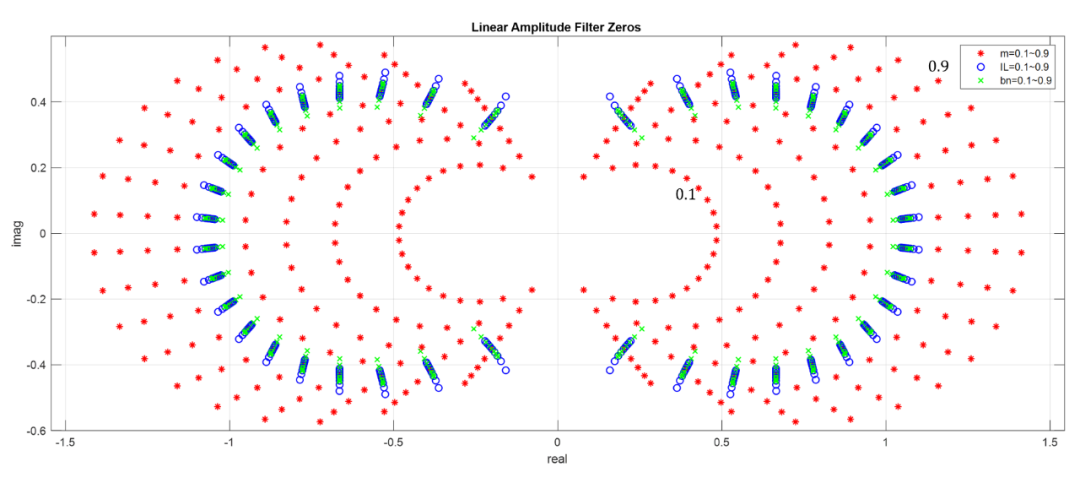
当滤波器阶数非常高时就极点分布规律就非常明显（以下展示100阶滤波器极点分布）：

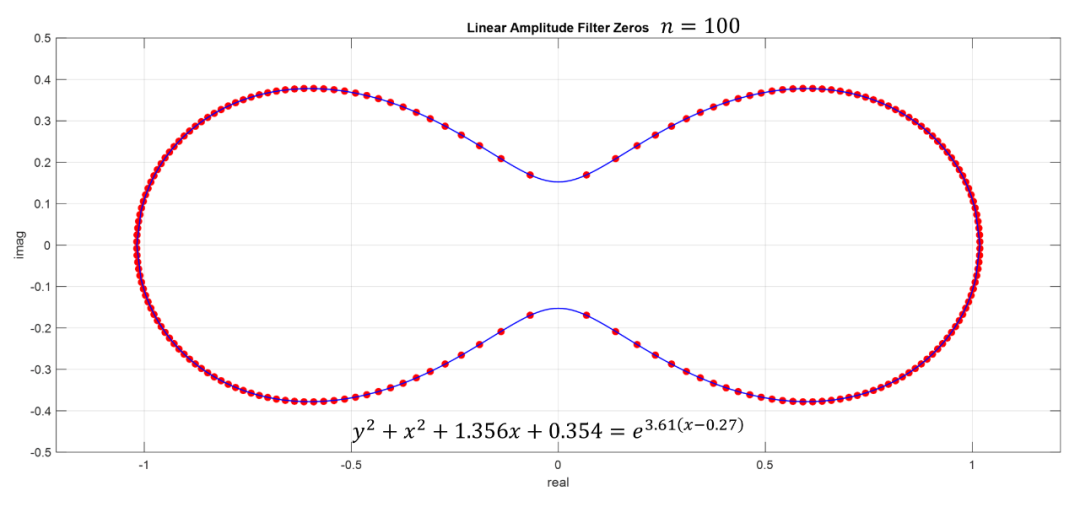
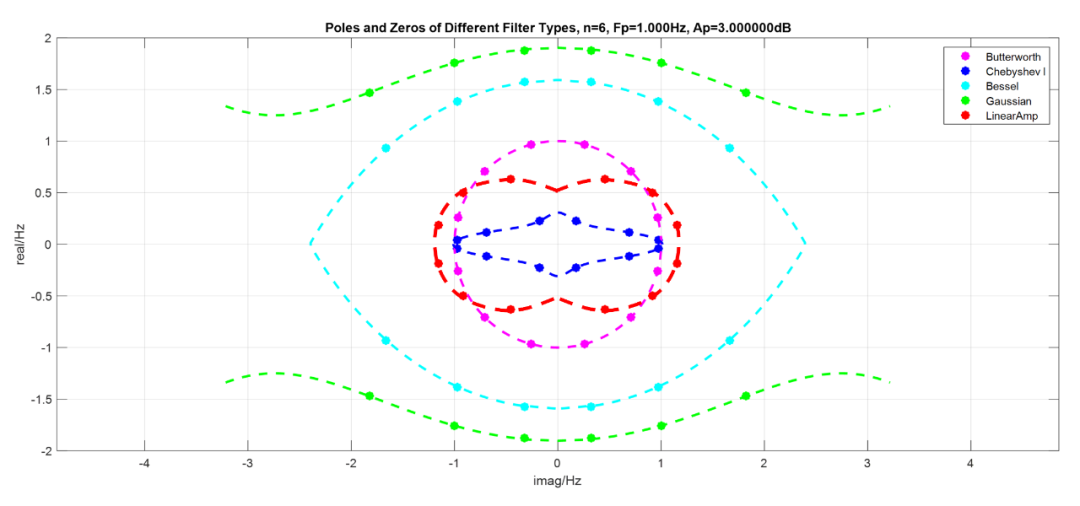
下图是不同类型滤波器的零极点分布图，红色曲线和点是6阶直线幅度滤波器极点分布：

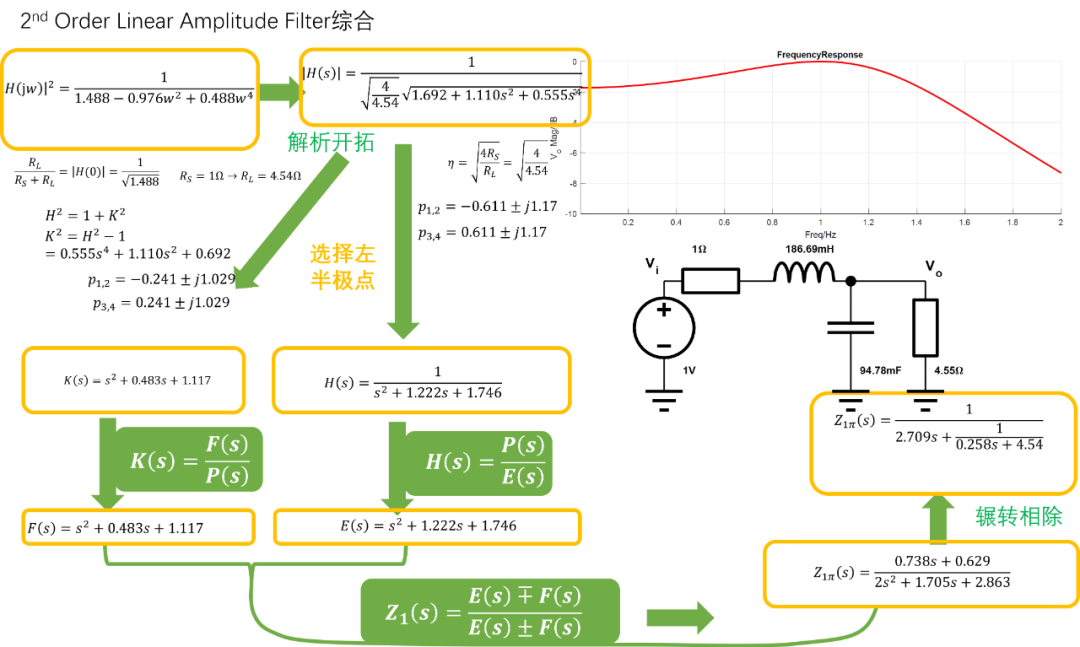
直线幅度滤波器综合

这里仅使用全极点滤波器来综合，列出一个简单的2阶3dB直线幅度滤波器综合实例，以供参考：

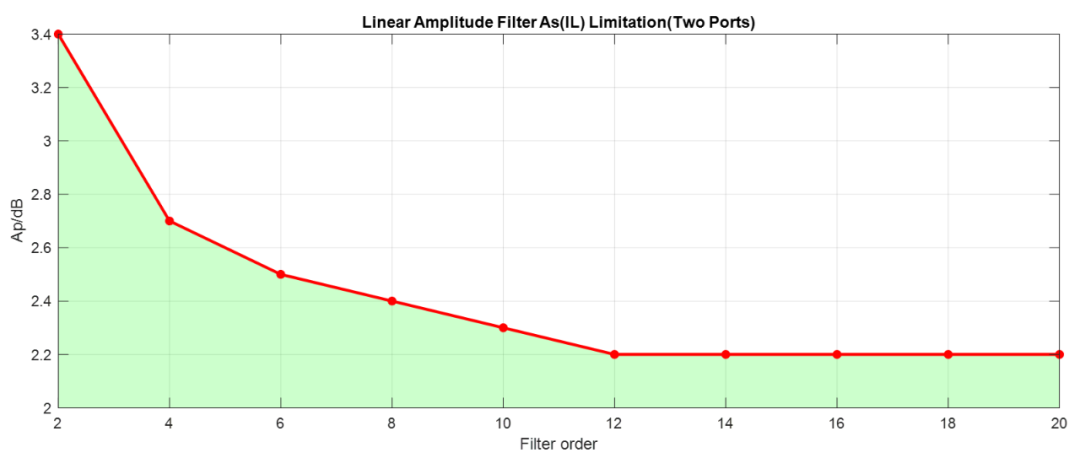
直线幅度滤波器IL(As)限制

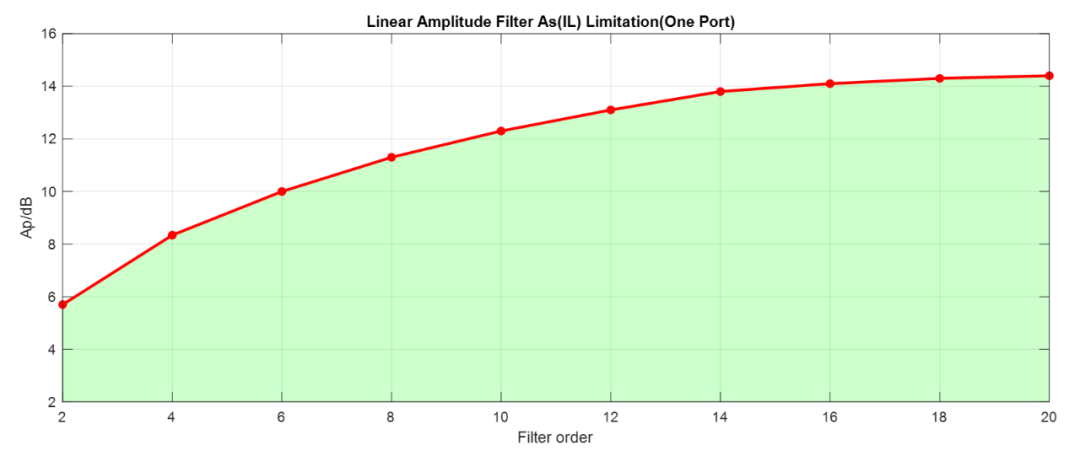
对于上述线性幅度滤波器，由于综合实现方面的限制，对于两端匹配线性幅度滤波器，只能满足特定IL(As)目标，比如对于2阶线性幅度滤波器，其As必须小于3.4dB，对于10阶线性幅度滤波器，其As必须小于2.3dB。

具体如下图所示(图中阴影部分是可实现的部分)：

但是对于单端匹配状态下的线性幅度滤波器，可以综合出来的幅度调整范围就宽很多，如对于终端开路的直线幅度滤波器，假设，那么可以得到如下的综合结果：

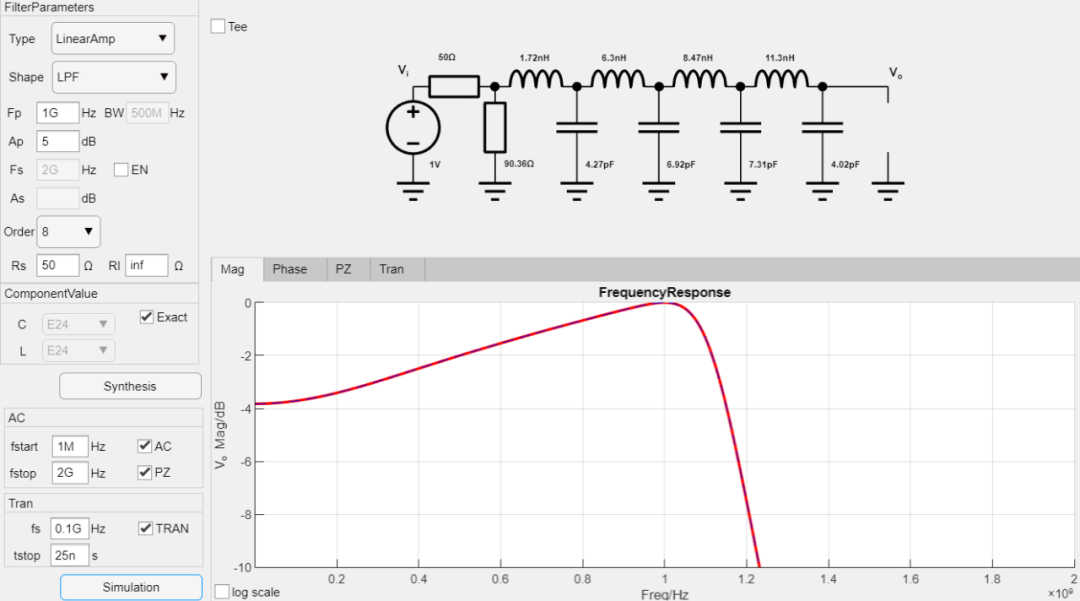
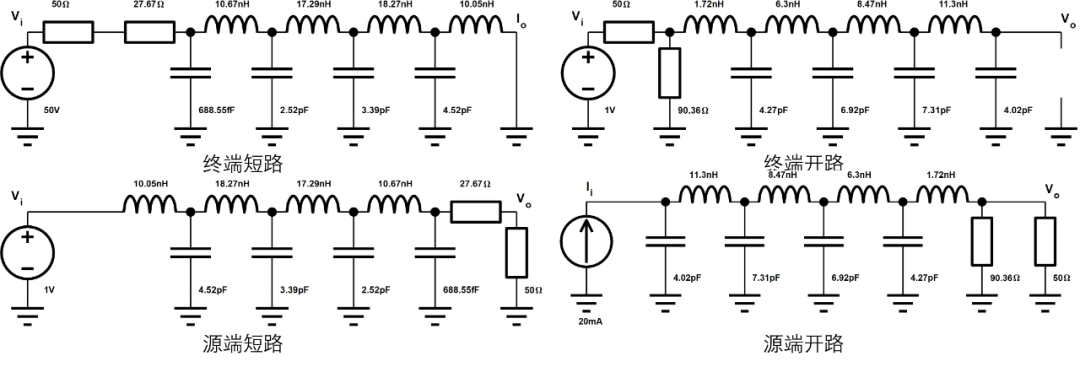
同样的参数4种不同终端情况汇总如下，均可以综合出实际的电路出来：

当然两端口直线幅度综合限制也是有的，如下所示(图中阴影部分是可实现的部分)：

直线幅度滤波器设计软件

基于Matlab的appdesign工具开发了一套滤波器设计软件, 主要特点是：

支持直线幅度滤波器(Linear Amplitude Filter)、勒让德滤波器(Legendre Filter)、高斯滤波器(Gaussian Filter)、贝塞尔滤波器(Bessel Filter)、椭圆函数滤波器(Elliptic/Cauer Filter)、切比雪夫滤波器(Chebyshev I)、逆切比雪夫滤波器(Chebyshev II, Inverse Chebyshev)、巴特沃斯滤波器(Butterworth)设计

支持4种不同滤波器通带类型(LPF,HPF,BPF,BRF)设计

T型和PI型结构滤波器随意切换

可以设置阻带衰减决定滤波器阶数

可以设置通带衰减来综合滤波器

可以随意配置负载和终端阻抗, 并支持一端接载(源端电阻短路, 源端电流源, 终端开路, 终端短路)设计

可以幅频响应分析、零极点分析、瞬态分析

可以显示理想频率响应、零极点和实际仿真的的频率响应、零极点

可以支持实际标准器件逼近设计

LinearAmp LPF设计举例

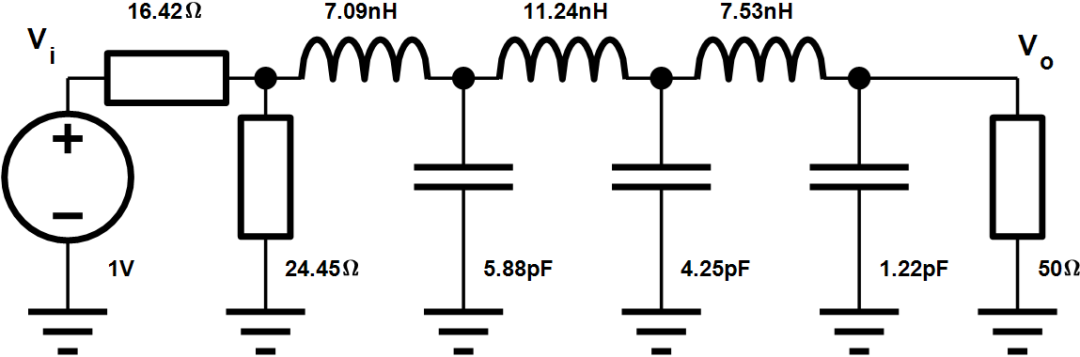
设计一款-2.0dB截止频率为1GHz, 8阶低通线性幅度滤波器，输入输出阻抗为50欧姆，设计过程如下：

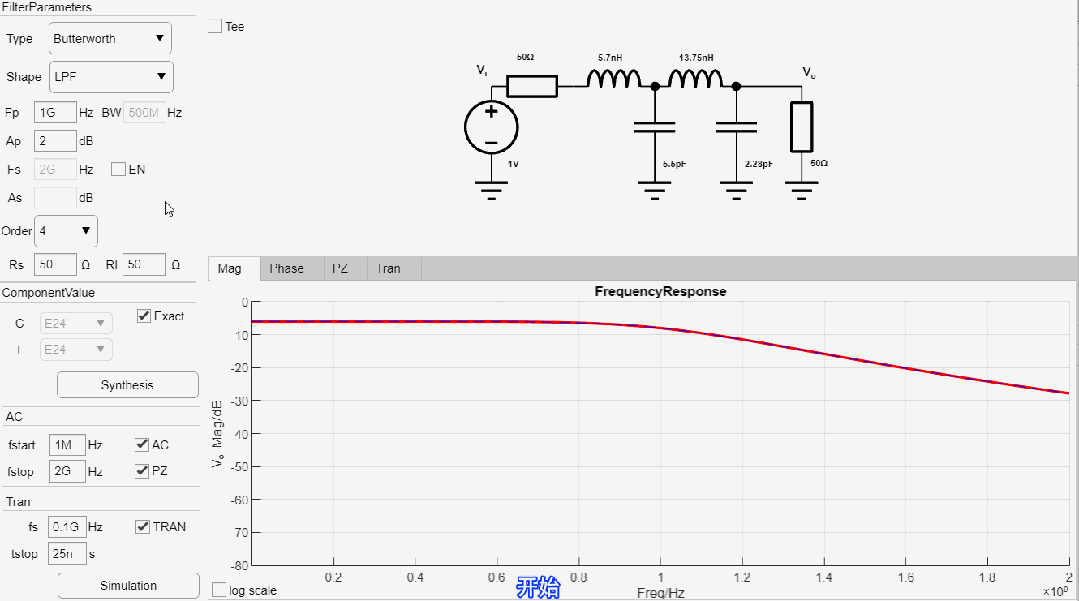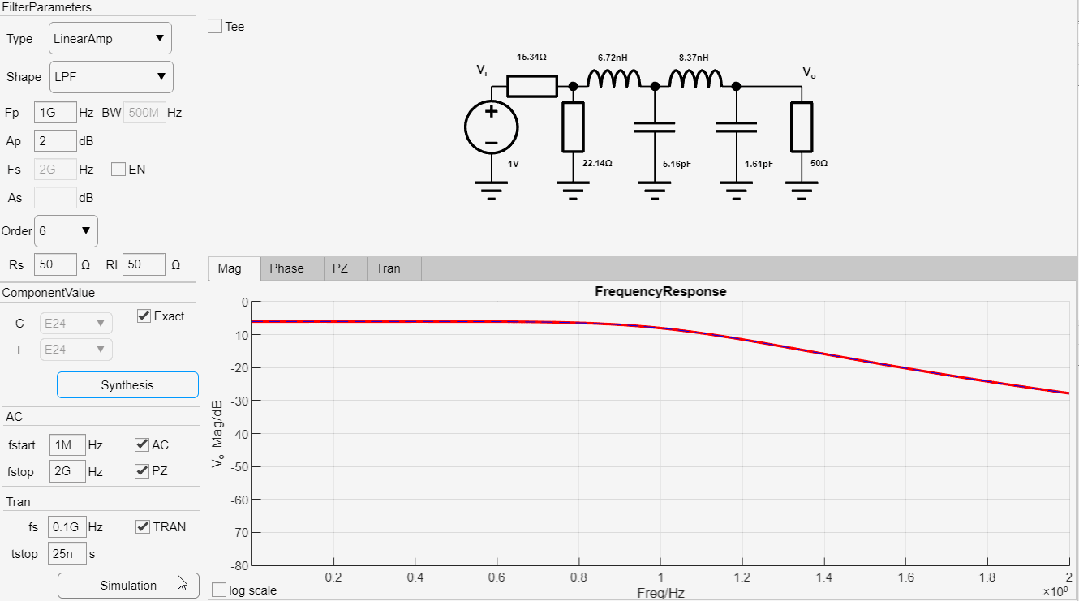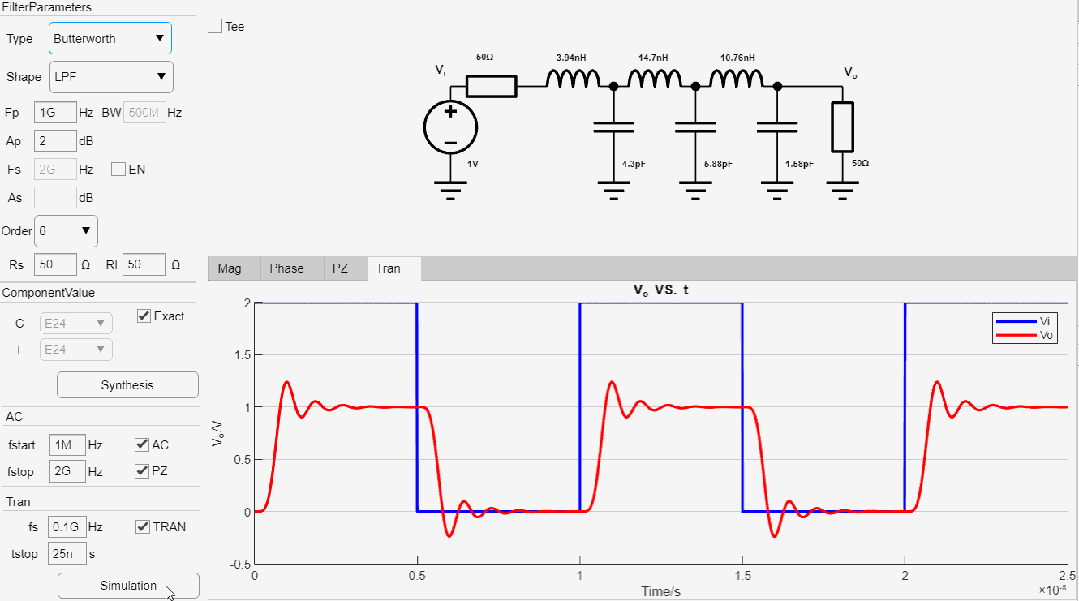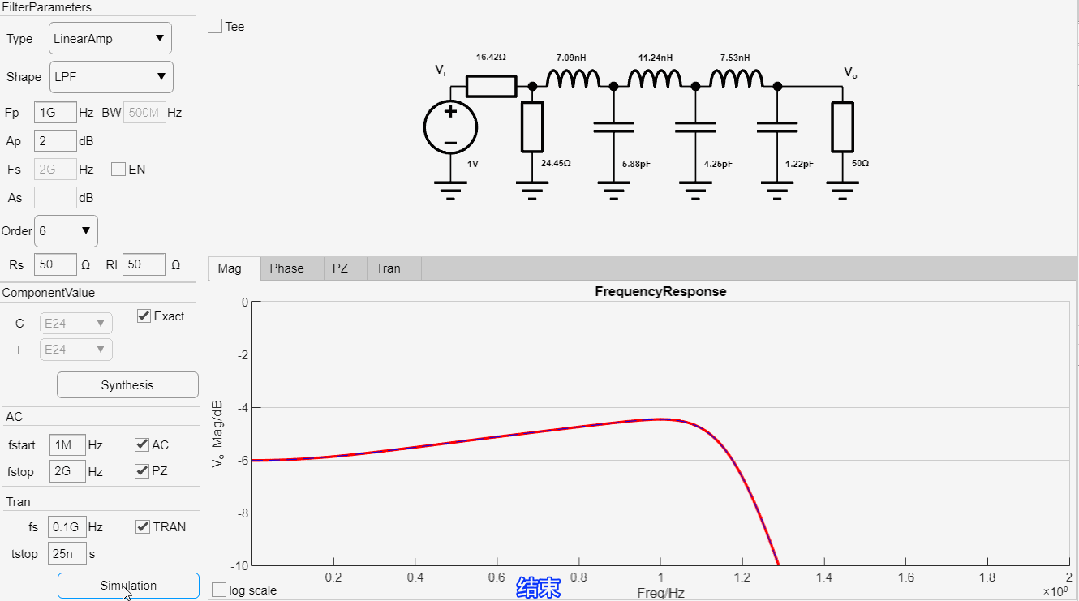
最终设计参数如下：

线性幅度滤波器瞬态仿真结果：

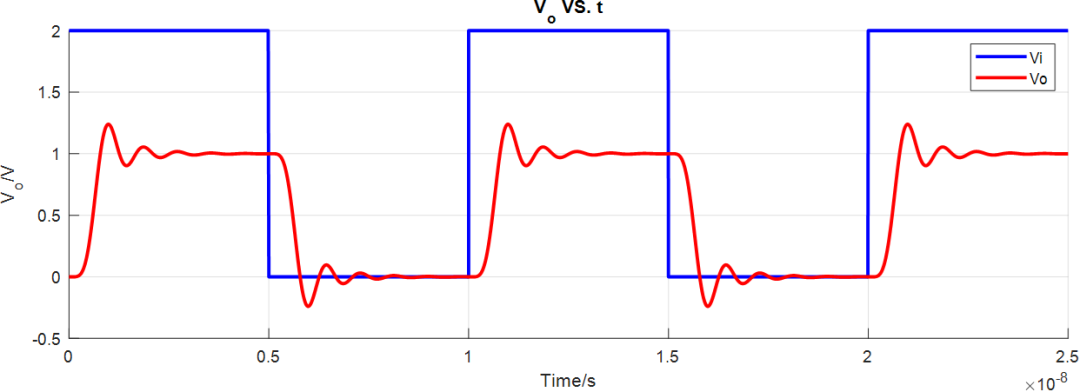
线性幅度滤波器AC仿真结果：

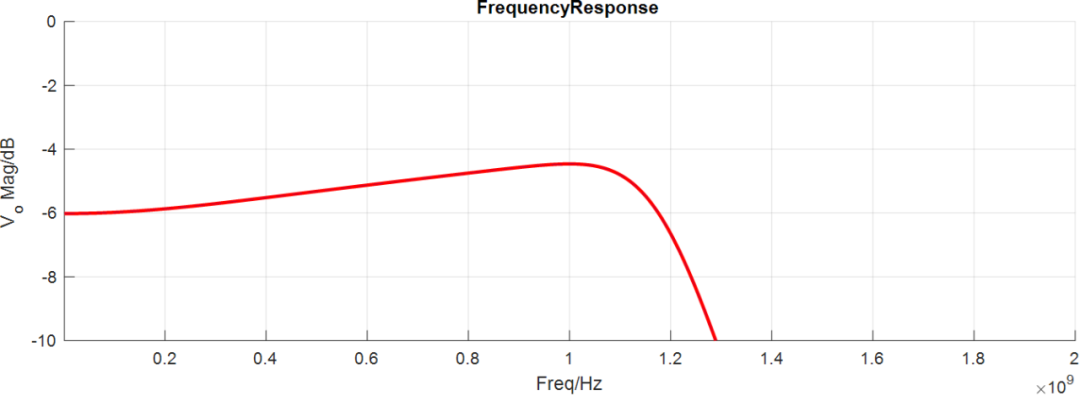
程序的Matalb源码已经上传GitHub中(https://github.com/etools361/MatlabLinearAmpFilterDesignApp)，有兴趣的同学可以下载试用体验，当然也欢迎技术交流。

展望

本文只提出了偶数阶滤波器的梯形网络实现方法，还可探索奇数阶滤波器设计；

理论上还存在多种不同实现方案，比如使用电阻和电容网络实现；

两端匹配衰减幅度的范围也可以进一步拓宽；

匹配特性还可改善，比如将对地电阻衰减更换为衰可以进一步改善驻波；

　　审核编辑：汤梓红