基于FFT的DSSS序列偶捕获

 

　　在直接序列扩频通信中，使用PN码与信号相乘将信号带宽扩展，这样如果仍然使用传统的接收机将无法恢复信号。所以在接收端，用于发射端扩展用的相同的伪随机序列对接收到的扩频信号进行相关处理，恢复出原来的信息。干扰信号由于与伪随机序列不相关，在接收端被扩展，使落入信号频带内的干扰信号功率大大降低，从而提高了系统的输出信噪比，达到抗干扰的目的。由此可见，扩频码在直扩系统中的作用十分重要，在一般情况下，PN码的选取遵照接收端和发射端必须使用完全相同的PN码(即PN码要求同步)才能完成扩频解扩。但是扩频码在发射端和接收端可以使用不同的扩频码，只需要满足一定条件即可。所以满足扩频解扩要求序列偶可以应用于直扩系统中。

　　1 序列偶

　　序列偶是一维数组，假设给出一组最佳序列偶X=(x0，x1，x2，…，xN-1)和Y=(y0，y1，y2，…，yN-1)，N为长度，组成一组最佳序列偶(X，Y)，它们是双极性的，所以X和Y中的取值为“+1”或“-1”。二者的互相关函数为：

　　

 

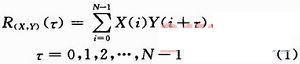
　　若τ=0，则称R(X，Y)(τ)为同阶自相关或自相关主瓣宽度，同理若τ≠0，则称R(X，Y)(τ)为不同阶自相关或自相关旁瓣宽度。最佳序列偶其旁瓣的自相关函数值为0。PN码的相关性是广泛用于扩频通信中的关键，而最佳序列偶便是具有性能优越的自相关性，使其可以被广泛应用在扩频通信中。例如：X=+1+1+1-1-1-1+1+1+1-1-1-1-1+1+1+1-1-1-1-1，Y=+1-1+1+1-1+1+1-1+1-1-1+1-1-1+1-1-1+1-1-1。根据公式得到最佳序列偶的相关值为

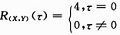
，其主瓣值为4，旁瓣值为0。X的自相关值RX(0)=20，其他为13，11，10，8，7，5，4，3，2，1和0;Y的自相关函数值与x的相同。虽然(X，Y)的相关性不是理想的，但其相关性性能方面有了极大的提高。然而在直扩系统中，若扩频码的次大相关值比较大时会影响到相关峰值的捕获，进而导致PN码不同步，因此性能优越的自相关性在直扩系统中起着重要作用。为了研究比较最佳序列偶和GOLD码及m序列的自相关特性，假设(X，Y)=(4E23E944，4623E944)，GOLD码为(74FAB3AA)，m序列为(483E3750)，序列均采用十六进制，转换为二进制后“1”代表“1”，“0”代表“-1”，自相关值为负时，也会影响到对最大相关值的判断，所以要将其考虑进去。由图1可以看出，当序列长度相同时，m序列的自相关性最好，最佳序列偶的自相关性比GOLD码的好，不仅最大相关值小于GOLD码，而且次大值也同样小于GOLD码，最佳序列偶的最大相关值与次大相关值之比为6/29=0.206 9，而GOLD的为9/31=0.290 3，所以本文认为最佳序列偶自相关性能优于GOLD码。序列偶就是以削弱主峰来换取对旁瓣的抑制，所以自相关性能的排序为m序列、序列偶、GOLD码。

 

　　

 

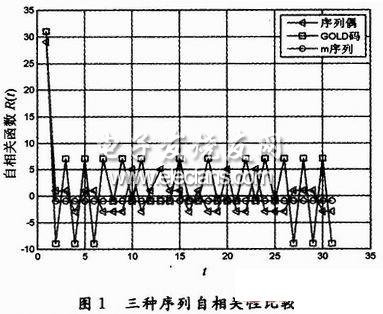
　　既然序列偶的自相关性优于GOLD码，则它可以应用到DSSS中，只是与一般的DSSS不同的是，序列偶的X用于扩频，Y用于接收端解扩。

　　下面可以对序列偶用于扩频的过程进行数学分析。设传输信号为：

　　u(t)=Acd(t)X(t)cos(2πfct)

　　式中：d(t)是基带信号;Ac和fc是调制载波的振幅和频率。接收信号r(t)=Acd(t)X(t)cos(2πfct)+i(t)+n(t)，其中i(t)=Acos(2πfIt)为正弦波干扰信号;n(t)为噪声，对信号解调解扩：

　　

 

　　当系统处于有正弦干扰的环境时，使用序列偶的误码率性能优于m序列和GOLD码。若没有正弦干扰则序列偶的性能最差。

　　下面研究序列偶这种比较新的理论用于猝发式直扩系统中。

　　2 DSSS序列偶捕获

　　2.1 基于FFT序列偶捕获算法

　　采用基于FFT的伪码捕获方案，具体搜索过程描述如下：本地载波对准初始频率估计值，这样就能使产生的信号对准一个频率搜索单元，系统启动FFT捕获环路，程序通过找出所有的相关峰值，对其进行比较找出其中相关峰值的最大值，如果最大值大于已经设定的检测门限时，表明信号捕获，得出信号所在位置载频和码相位，系统进入跟踪阶段。反之则表明信号未捕获，可以控制逻辑来改变频差搜索单元，再次重复以上过程。在理想状态下，码相位若按照Tc/2搜索，且在所有载频估计单元内完成搜索，则FFT并行捕获系统比串行捕获系统的搜索速度快2N倍，可实现快速捕获目的。算法描述如下：

　　(1)设置参数，包括数据速率为10 Kb/s;调制方式为BPSK或QPSK调制;扩频处理增益为31;抽样频率为40 MHz;载波频率为10 MHz;每bit采样点为4 000。

　　(2)生成数据，包括产生一组随机数，CRC校验，卷积编码，单极性变为双极性，加入位同步头，帧同步头。

　　(3)生成扩频码，采用序列偶，码长为31。

　　(4)选择调制方式，若是采用QPSK，则数据先串并变换，若为BPSK则不需要串并变换。

　　(5)计算每bit采样点为4 000，获得1 b采样点内序列偶，每chip采样点为4。

　　(6)扩频，同时计算下1 b内序列偶初相。

　　(7)计算各采样点载波相位、调制信号，同时计算下1 b内载波初始相位。

　　(8)调制信号进入高斯白噪声信道。

　　(9)通过信道信号进行FFT变换取共轭。

　　(10)本地PN码及本地载波信号相乘得到信号进行FFT变换。

　　(11)两信号进行IFFT后进行码相位一多普勒频移值二维搜索。

　　(12)搜索比较所有相关峰值，若有超过门限即最大相关峰，实现捕获，停止搜索，启动跟踪电路;若失锁产生跟踪脉冲调整产生序列偶的本地时钟，直到同步锁定。

　　(13)得到序列偶相位及多普勒频移值，进行解调，通过抽样判决取样，进行滚降滤波后再进行序列偶解扩。

　　(14)位同步帧同步，卷积译码，恢复数据。

　　2.2 仿真分析

　　实现序列偶捕获的相关峰值输出，当系统完成序列偶捕获以后，就会输出一个最大相关峰。仿真得到误码率如图2所示，它和系统采用解调方式及扩频增益有关，相干解调误码率性能优于差分解调，高扩频比优于低扩频比，误码率要低于10-3以下，信噪比要大于8 dB，扩频增益越大，误码率越低，扩频增益足够大的时候，在一定信噪比情况下可以得到很小的误码率。图3表明高扩频比优于低扩频比。

　　

 

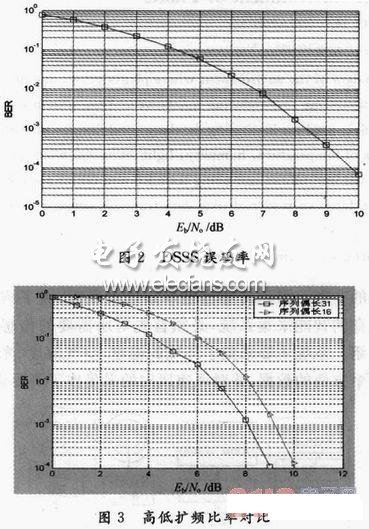
　　3 结语

　　本文重点研究了序列偶的自相关特性和m序列及GOLD码对比分析，并且研究了将序列偶用于DSSS系统中的PN码捕获问题，提出了捕获算法的思路并且仿真实现。虽然序列偶并不是最佳的，但是若能找到一种最佳的序列偶，那么它会比其他的PN码具有更高的应用价值，可以应用于各个领域如CDMA系统。