

交流电的有功功率、无功功率和功率因数你知多少?
电子说
描述
1
交流电的有功功率、无功功率和视在功率
交流电路中功率的计算远比直流电路复杂。就其负载而言,就有纯电阻、纯电感、纯电容和感性、容性等多种,生活中较常见的有接近于纯电阻的负载(例如白炽灯、电炉、电热水器和电烙铁、电熨斗等)和感性负载(最常见的是各种电动机,另外还有荧光灯、电视机、微波炉等)。
纯电阻负载产生的功率叫做有功功率 ,用符号P表示,基本单位为瓦特(W),较大的数值用千瓦(kW),它是实实在在地将电能转化成了其他的能量,例如热能、光能或机械能等。
**纯电感负载和纯电容负载只起储存和释放电能(在这一过程中,也会有能量的转化问题)的作用,并不消耗电能。所以将这种功率叫做无功功率。**无功功率的符号为Q,基本单位为乏(var)。
感性负载是电路中同时存在电阻、电感的负载,也包括还存在电容负载,但电容的作用小于电感负载。这种负载在生活中最常见。
容性负载是电路中同时存在电阻、电容的负载,也包括还存在电感负载,但电感的作用小于电容负载。
**当交流电流通过上述感性负载或容性负载时,将产生三种不同的功率,即视在功率、有功功率和无功功率。**这三种功率的数值关系和向量关系刚好是一个直角三角形,其中有功功率和无功功率分别是两个直角边,视在功率为斜边。该直角三角形被称为交流功率三角形。
表示视在功率的斜边和表示有功功率的直角边之间的夹角φ叫功率因数角,简称为功率角。它是电路总电流滞后(对于感性负载)或超前(对于容性负载)于电路端电压的相位差角,如图1所示。
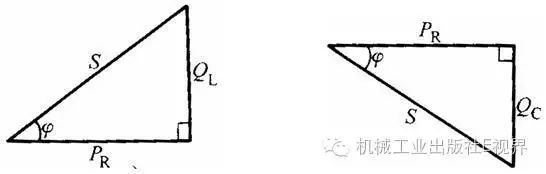
a)只有电阻和电感 b)只有电阻和电容

c)三种负载都有,但感性负载大于容性负载 d)三种负载都有,但容性负载大于感性负载
图1 正弦交流电功率三角形
功率因数角的余弦(即cosφ)被称为功率因数。它是交流电路中一个很重要的参数,也是交流用电设备的一个重要性能参数。
由图1可以得出如下关系式(用于单相电路):

式中 I—— 电路的总电流; U—— 电路的端电压。
2
交流电路功率因数的定义和常用计算方法
功率因数在数值上等于有功功率与视在功率的比值,这里的视在功率可理解为总输入功率,从这一点上来说,功率因数就是总输入功率的有效利用率。
在一定意义上来讲,功率因数也表示了电源功率的利用率。
得到功率因数的最直接方法是使用专用仪表进行测量,该仪表被称为功率因数表或相位表;否则,要用仪表测得电路的输入有功功率P、电流I和电压U,然后用公式计算求得。
用后一种方法时,对单相电路(包括三相电路中的某一相),所用公式较简单,即有功功率P(W)除以电压U(V)乘电流I(A),对于三相电路,应为被求相的相电压和相电流:

即口诀“有功除以压乘流”。
对于三相负载平衡的电路,若求三相的功率因数,则应求出三相的总有功功率P(W)、线电压平均值U(V)和线电流的平均值I(A),然后用下式进行计算。

即口诀“三相电路负载平,测取线压和线流,三相有功做分子,根三、压、流做分母”。
当使用相电压平均值Uφ(V)和相电流的平均值Iφ(A)时,将上述公式分母中的根号3改为3即可。即

举例
【例1】某单相交流电路负载的有功功率为1kW,负载电压和电流分别为220V和5.8A。求其功率因数。
解:已知条件是P=1kW=1000W,U=220V,I=5.8A。求cosφ=?
根据计算单相负载功率因数的口诀“有功除以压乘流”,可得

答:功率因数为0.7837。
【例2】某三相平衡的交流负载输入有功功率为4.5kW,负载三相线电压和线电流的平均值分别为380V和8.2A。求其三相功率因数。
解:已知条件是P=4.5kW=4500W,U=380V,I=8.2A。求cosφ=?
根据已知线电压和线电流计算三相负载功率因数的口诀“三相电路负载平,测取线压和线流,三相有功做分子,根三、压、流做分母”,可得

答:功率因数为0.8338。
3
用并联电容提高感性负载电路功率因数的计算方法
提高电路功率因数的意义在于提高电源的利用率、减小无功电流在线路中产生的热损耗和电压损失,提高电路的总体效率。
由于用电设备中,绝大部分是感性负载,所以电路的功率因数也都会小于1(滞后,即电流相位滞后于电压相位),在某些用电场合,还不到0.5,这会造成电能和电源设备的大量浪费。因此应设法提高。
**提高功率因数的常用办法是在负载两端并联电容器。**其原理是利用电容与电感的电流在相位上刚好相差180°(方向相反),可以相互交换无功电流,从而减少从电源中再摄取无功电流造成的电源浪费以及由此造成的线路热损耗和电压损失。
设负载的功率(有功功率,以下内容中不特别指出时,均指有功功率)为P(单位为W),相电压为U(单位为V),电源频率为f(Hz),当时的功率因数为cosφD,预计提高到的功率因数为cosφG,则需并联的电容器容量C(F)为

当电源频率f=50Hz时,上式中的2πf≈314(即口诀中所说的“再除三一四得商”中的“三一四”)。上式即变为

上式即后一部分口诀所描述的内容,其中的两个正切值是由当时的功率因数(下角标用D)和预计达到的功率因数(下角标用G)通过反三角函数求得各自的功率因数角(口诀中说“反角函数求角度”)后再计算得到的。
若功率P的单位为kW,电容量C的单位为μF,则
(1)当电压U=220V时,上式将进一步简化为
C=65.8P(tgφD-tgφG)
(2)当电压U=380V时,上式将进一步简化为
C=22P(tgφD-tgφG)
这就是口诀的第三部分“功率单位用千瓦,电容单位用微法,功率乘以正切差,再乘系数看电压。单相电压二百二,系数六十五点八;系数若为二十二,电压数值三百八”所描述的内容,其中的“正切差”即是前面口诀中讲述的两个正切值之差。
举例
某感性负载,其额定功率为1.1kW,接在电压为220V、50Hz的电源上工作时,电路的功率因数为0.5。若想将功率因数提高到0.8,求需并联多大容量的电容器?
解:由题意可知:P=1.1kW=1100W,U=220V,f=50Hz,cosφD=0.5,cosφG=0.8,则需并联的电容器容量C为可用公式求取:
用反三角函数先求出现有功率因数为cosφD=0.5的功率因数角φD=60°,再求出该角的正切值tgφD=tg60°=1.732,即口诀中所说的“先知现有功因数,反角函数求角度,求出该角正切值,作为上面第一数”。
再求出预计提高到的功率因数为cosφG=0.8的功率因数角φG=36.9°,tgφG=tg36.9°=0.751,即口诀中所说的“再设预想功因数,同样方法求角度,也求该角正切值,作为上面第二数”。

直接用公式得:
C=65.8P(tgφD-tgφG)=65.8×1.1(1.732-0.751)=71μF
答:需并联容量为71μF的电容器。
-
有功功率和无功功率的区别和特点2018-07-27 11493
-
电源技术之无功功率教程2020-09-23 3928
-
功率三角和功率因数教程2020-09-25 6630
-
电功率你理解透了吗?怎么算功率因数?2021-07-09 730
-
三相交流电路的功率也分有功功率和无功功率吗2021-09-14 2373
-
交流电路的功率和功率因数2008-09-25 8586
-
无功功率与功率因数补偿方式2021-03-16 6836
-
有功功率与无功功率有什么关系2023-01-30 11019
-
国网智能电表视在功率kVA、有功功率Kw、无功功率kVar的区别2023-04-12 2479
-
电路的功率因数怎么计算 功率因数偏低如何解决2024-02-14 7835
-
功率因数和有功功率无功功率的关系2024-01-19 12674
-
提高功率因数进行无功功率补偿有什么意义?无功补偿有哪些方法?2024-01-22 2598
-
为什么补偿无功功率因数会提高?功率因数低如何补偿?2024-01-23 3635
-
功率因数偏低如何解决 功率因数和有功功率无功功率的关系2024-02-04 19168
-
无功越高功率因数越高吗2024-03-06 2561
全部0条评论

快来发表一下你的评论吧 !

