基于内点法-退火因子法的主动配电网无功优化

大规模分布式电源(distributed generation，DG)接入主动配电网对配电网的潮流、节点电压和网络损耗有很大的影响。在主动配电网(active distribution network，ADN)中，具有一定的功调节能力。本文研究了风力发电、光伏发电和其他DG的有功功率与无功功率的关系，结合传统的电压调节方法，对有源配电网的潮流进行了优化。根据DG的有功功率预测，动态调整DG的无功出力，以保持局部电压稳定，实现最优分配。

一

DG无功特性

正栅极耦合变换器反映基本的无功供电能力。整个DG 单元决定了有功功率的可控范围和最大无功功率的可用性。DG 在提供无功功率的能力时，需单独分析网格耦合转换器和DG 单元[12]的其余部分。定性总结了不同的网格耦合技术时的针对无功功率控制、直流电压控制、电压增量和故障穿越4种状态[2]，对比结果如表1 所示。

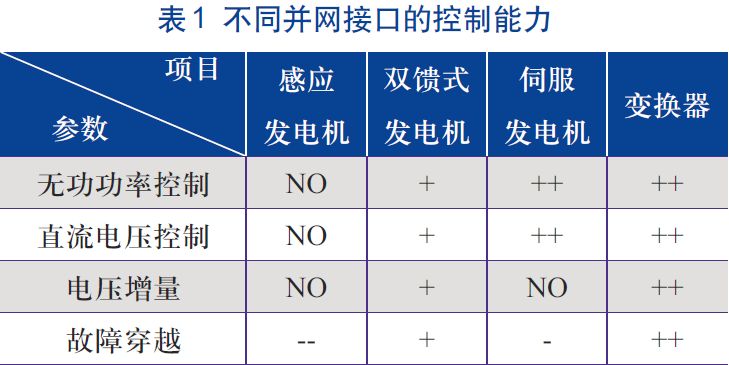
** 备注：++ 表示有极好的能力，+ 表示有较好的能力，-表示有少量能力，-- 表示有极少的能力，NO 表示不存在此情况目前，DG 主要以风力发电和光伏发电为主。本文在DG 并网技术的基础上，重点对双馈式风力发电系统与光伏发电系统的无功功率特性进行了研究。**

1.1

双馈式风力发电机功率特性

双馈式风力发电机无功功率特性受定子绕组、转子绕组和转子侧电流等因素的影响[13]，其中转子侧电流最大值对无功功率运行范围起到主要作用。电网侧转换器的无功功率输出原则上可以独立于有功功率输出而进行控制，但不会超过视在功率。

在约束条件下，风力发电机最大无功输出功率Qmax 与有功功率P、最大视在功率Smax 的关系如式(1)所示：

双馈式风力发电机的机械和电气特性在很大程度上取决于转差率，转子的有功功率与转差率成正比。因此，风力发电机的无功功率容量也取决于转差率，式(1)可简化为：

式中， s 为风力发电机定转子转差率， Ptot为总功率，另外则表示总功率受限于转差率。

风力发电机的总功率是定子功率和有效转子功率之和。转差率受限于转子电压，因此转差率不会太高，同时会进一步降低无功功率Qmax 。

由此可得双馈式风力发电机的P-Q 曲线，如图1 所示。

1.2

光伏发电系统功率特性

并网光伏系统可向电网注入有功功率或无功功率，并入电网后的电压关系为：

式中， PPV、QPV 分别为光伏系统注入电网的有功功率、无功功率； Pload、Qload 分别为负载的有功功率、无功功率；V0 为初始电压；Vs 为计算电压；Rs 为光伏系统电阻；Xs 为光伏系统电抗。

当并网点电压发生△u 的增量变化时，则相应发生△i 的增量变化，则：

式中， ΔPPV 为光伏系统有功功率变化量；ΔIQ 为光伏系统无功电流变化量； φ 为等效阻抗角； θ 为光伏并网系统功率因素角； Sk 为视在功率。 逆变器发出的无功功率的约束条件为：

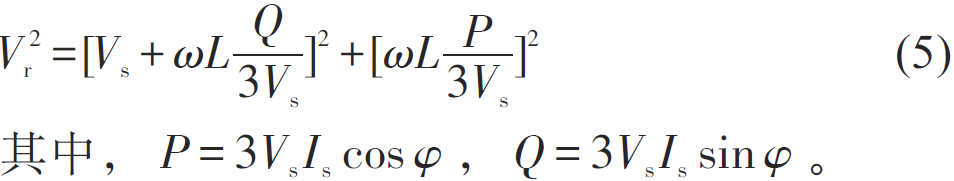
式中， Vr 为逆变器输出电压； Vs 为逆变器输入电压； ω 为相位旋转速度； L 为光伏系统电感； P 为光伏系统有功功率； Q 为光伏系统无功功率； Is 为输入电流。 系统无功约束条件为：

式中， Vdc 为直流输入电压。 逆变器容量约束条件为：

式中， S 为逆变器视在功率。 由此可得光伏功率特性图，如图2 所示。

式中，F 为目标函数；Ploss 为有功功率损失；△Vad 为i 节点的电压增量， V * i 为i 节点参考电压； γ1、γ2 为分布系数。 潮流约束条件为：

二

主动配电网无功优化数学模型

主动配电网在综合考虑系统的可靠性和经济性前提下，有功与无功协调控制通过优先DG 进行自我调节。考虑到主动配电网的全局最优性，本文以有功网损和系统电压偏移作为无功优化指标，并利用固定权重的方法将多目标优化问题转化为单目标优化问题，考虑到系统节点电压和发电机无功出力易出现越界的情况，引入高斯罚函数构建模型，如式(9)所示。

** 式中， PDG,i、QDG,i 分别为节点i 注入电网的有功功率、无功功率； Pik、Qik 分别为节点i 处的第k 台发电机组输出的有功功率、无功功率； Vi、Vj分别为i、j 节点电压幅值； θij 为电压相角差；**

Gij、Bij 分别为线路的电导、电纳； N 为节点数；δij 为线路相角差； QCi为节点i 的无功补偿；

式中，VGi 为i 节点注入电压；KTi 为电源频率；Qci 为并联电容器补偿容量； Vi 为i 节点的电压； QGj 为j 节点注入的无功功率。 DG 运行约束条件为：

三

模拟退火罚函数的解决方法

本文采用在原对偶内点法控制策略中引进高斯罚函数，以实现离散变量连续化；与非连续罚函数相比，高斯罚函数有连续可微的优势；而模拟退火惩罚函数[14-16]可以避免在高斯罚函数中陷入局部最优，从而达到全局最优化。

因此，本文提出了逐步翘曲与参数测试相结合的策略[17]。基于高斯罚函数法、模拟退火罚函数法、原对偶内点法，设计了一种求解离散变量无功优化问题的实用算法。相关参数的选择如下： Fmin 表示各变量连续过程所得到的目标函数的最优解；初始罚系数λ0 =10-5Fmin；M=105；邻域大小因子σ =0.25nd 。在求解过程中，离散控制变量分为松弛部分和固定部分。松弛部分是指连续的离散变量，其指数集表示为Islack；固定部分是指被翘曲化的离散变量，其指数集表示为Ifix。

设计的算法步骤如下：

1)初始化内点法[18-21]，设定λ =0，忽略离散控制变量的罚函数不翘曲。得到了连续过程中各变量的最优解(x*,uc,ud)T 和最优目标Fmin。

2)设置k =1,ν(k -1) =10-5Fmin ，整数ud 的范围为[U- ] d,Uˉd ，计算邻域中心vdi =|u | di +0.5，设置邻域大小因子σ =0.25nd，翘曲阈值为δ，惩罚系数增长因子β =2.5，迭代初值(x(0),u（0）c ,u（0）d )= (x*,u*c,u*d)T 。

3)设定(x(k),u（k）c ,u（k）d )=(x(k -1),u(k -1)c ,u(k -1)d )T ，它可以作为迭代初值。用高斯罚函数和原对偶内点法求解引入惩罚项的最优问题，同时启动模拟退火惩罚项，比较高斯惩罚函数与模拟退火惩罚函数取最优值，获得(x(k),u（k）c ,u（k）d )=(x(k 1),u(k -1)c ,u(k -1)d )T 的最优解。

4)搜索离散变量u（k）d 的每个分量u（k）di 并对其进行分类。如果u（k）di ≤ -Ud +δ，那么i ∈Ifix，u（k）di =-Ud，如果u（k）di ≤ -Ud -δ，设置i ∈Ifix，u（k）di =Uˉd；否则设置i ∈Islack。

5. 如果没有新的范围下限Ifix，设置λ(k) =βλ(k -1)(β＞1) ，否则设置λ(k) =λ0。

6)如果Ifix =nd ，则跳到步骤7)；否则，设置k =k +1，跳到步骤3)。

7)验证最优解(x*,uc,ud)T 和最优目标Fmin，并输出结果。

模拟退火惩罚项计算步骤为：

1. 设定初始变量范围整数u*d 的范围为[U- ] d,Uˉd ，随机选定初定状态x0，计算模拟退火惩罚项p(x0) 。
2. 选取xr1,xr2,...,xrm 个绕动变量， △p(x)=p(x)-p(x0) 。

3)在温度参数T 下，重复一定次数的步骤2)，步骤3)。

4)逐渐降温， Tk +1 =αTk，0＜α＜1。

5)重复步骤2)，步骤5)，直到收敛。

四

算例

IEEE 14 节点分布系统的基础上，在配电系统3 台变压器设置有载调压变压器；添加3 个DG 和2 组并联电容器；线路参数和荷载参数不变。并联电容器的补偿容量与欠载分压容量(ULTC)比值范围是0.91.1，可分为8 档，步长为0.025。假设DG1 和DG2 是带有一定无功容量的光伏电源，分别连接到10 节点和13 节点。对于每个光伏DG，视在功率Sg =0.033p.u，有功功率输出Pg =0.03p.u；DG3 是一个有一定无功容量的双馈式风力发电机，并连接到4 节点，其视在功率Sg =0.4p.u，有功功率Pg =0.3p.u 。各个DG 的无功功率都满足无功约束方程。两组并联电容器的档位分别为0.06p.u ×(-14) 和0.05p.u ×(18) ，所有P、Q 点的电压范围是0.951.05p.u ，光伏节点的电压范围是0.9~1.1p.u 。

不同罚函数下无功优化结果最优解如表2所示，表2 中内点-高斯法、内点-退火法的最优解是指连续过程中所有变量的最优值。对比优化前与优化后可知， 整个系统的净损失从13.39MW 下降到9.35 MW，下降了30.17%。每个节点电压在约束条件范围内波动较小。因此，利用DG 的无功补偿能力，可为电网电压提供良好的支持，大幅降低能量损耗。

由表2 可知，数据功率损失由0.1339 降至0.0935，通过对比可发现，采用退火法优化有限的罚函数迭代，使高斯法能够跳出局部最优，进而达到无功功率优化，最终实现系统有功功率损失最小的目的。

根据最优化理论，引入罚函数的最优值大于或等于原连续问题的最优值，在罚函数处理上引进模拟退火罚函数防止高斯罚函数陷入局部最优。从这个角度分析，罚函数提高了松弛解的可行性，同时保持了最优解的折中。在无功就地控制方案的控制公式中，根据DG 参与电网辅助服务的目的，调整部分损耗，以维持局部电压稳定或为电力系统提供足够的无功功率。

五

结论

1)本文引进高斯罚函数法既保持了寻优的连续性，又将最优结果归整化，能够有效应用于无功优化离散变量归整问题。

2)本文在目标函数中引进模拟退火罚函数，既可以提高算法收敛精度和速度，同时有效解决了目标函数中只含高斯罚函数算法致使陷入局部最优的问题，得到全局最优结果。