

离散傅里叶变换DFT的定义及计算方法
电子说
1.4w人已加入
描述
3.1 背景
为什么需要定义一种“新”的变换?
计算机处理的两个基本条件:第一,只能处理离散的数据(时域和频域都要离散);第二,要有限长。
DTFT,时域上离散,但频域是连续的;DFS,时域频域都是离散的,但同时又都是周期的,周期序列长度为无限长。但同时我们也注意到,周期序列实际上只有有限个序列值有意义,因而它的离散傅里叶级数也适用于有限长序列,这就得到有限长序列的离散傅里叶变换(DFT)。
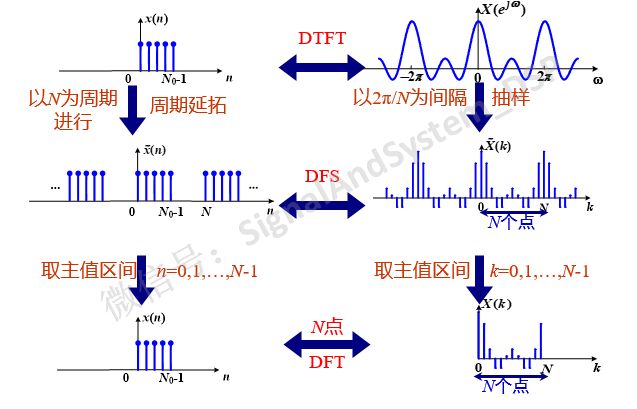
所以, DFT并不是一种新的变换 。它只是将DFS时域和频域上都取一个周期而已。**DFT正反变换的定义式与DFS相同,只是加了一个取值范围的限定而已。**换汤不换药。
3.2 DFT的定义及物理含义
重点:DFT与DFS、DTFT的关系


DFT不是序列x(n)的真正的频谱。x(n)的真正的频谱是DTFT,DFT只是对其真正频谱的一个周期上的离散抽样值。
3.3 DFT的计算
重点:DFT的两种计算方法。

下面的例题,分别用这两种方法进行求解。


对于本题来说,方法二特别直观,便于理解DFT与DTFT的关系。

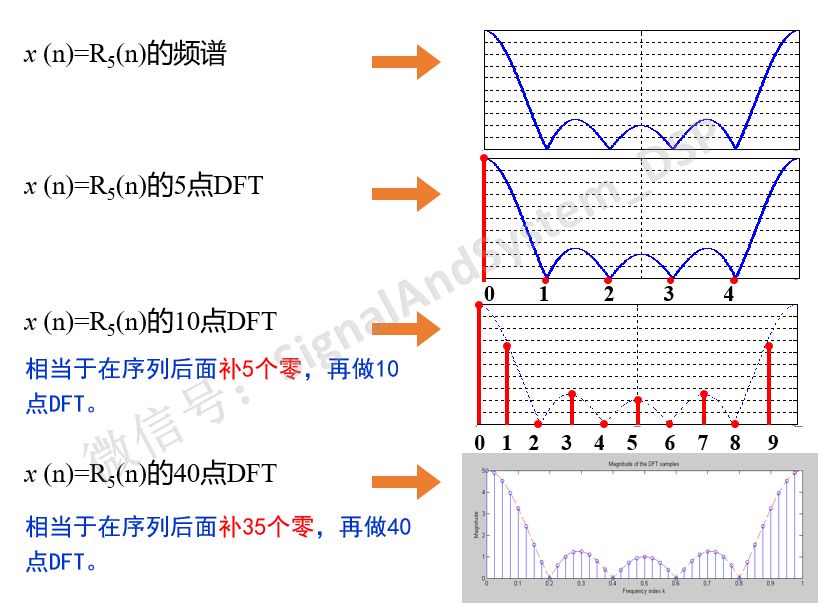
可见,同一个序列的不同点数的DFT,得到的结果不同。DFT的点数N越大,X(k)越能反映连续频谱的形状。
当DFT的点数N>序列的长度N0时,相当于在序列后面补上N-N0个零,故称为” 补零DFT “。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
DFT与离散时间傅里叶变换的关系 DFT在无线通信中的应用2024-12-20 2744
-
如何实现离散傅里叶变换2024-11-14 2287
-
傅里叶变换的实现方法2023-09-07 2298
-
Vivado中快速傅里叶变换FFT IP的配置及应用2023-07-20 6374
-
离散傅里叶变换DFT在电阻网络分析中到底起到什么作用2022-08-19 3059
-
利用快速傅里叶变换计算相关面2017-11-27 1838
-
离散傅里叶变换(DFT)及其快速算法(FFT)2016-12-28 1072
-
离散傅里叶变换,(DFT)Direct Fouriet Tr2009-07-25 2227
-
离散傅里叶变换及其快速算法2008-10-30 967
全部0条评论

快来发表一下你的评论吧 !

