

机器学习之人工神经网络(感知机算法)
人工智能
描述
如图一所示,神经元的MP模型输出y的表达式为:
y=φ(∑ωixi+b)=φ(ωTX+b)
其中,ωT=(ω1,ω2,…,ωi)T,X=(x1,x2,…,xi)。
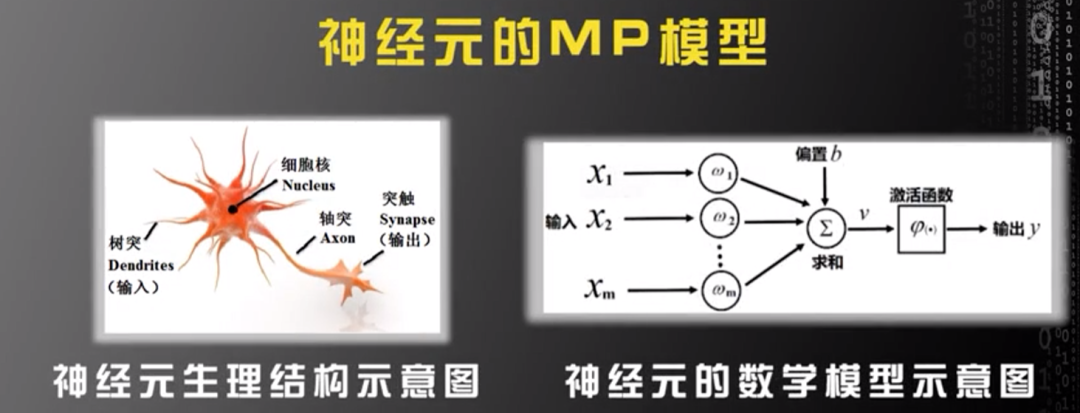
图片来源:中国慕课大学《机器学习概论》
1957年,弗兰克·罗森布拉特(Frank Rosenblatt)从数学角度考察MP模型,并提出可以通过若干成对的输入输出数据和机器学习方法获得ω和b的值,罗森布拉特依此提出感知机算法(Perceptron Algorithm)。
一、感知机的求解问题
求解问题为:假设二分类问题的输入为(Xi,yi),i=1~N,其中,Xi是训练数据,yi=±1,需求解一个向量ω和一个常数b,使得对i=1~N,有:
(1)若yi=+1,则ωTXi+b>0;
(2)若yi=-1,则ωTXi+b<0。
若训练数据满足上述条件,则称该数据获得平衡,否则该数据没有获得平衡。当训练数据没有获得平衡时,该数据满足:
(1)若yi=+1,则ωTXi+b<0;
(2)若yi=-1,则ωTXi+b>0。
若要求解可使所有训练数据均获得平衡的ω和b的值,则训练数据集需线性可分。
二、感知机的求解过程
(1)随机选择ω和b;
(2)取一个训练样本(X,y)
1)若ωTX+b>0,且y=-1,则:ω=ω-X,b=b-1;
2)若ωTX+b<0,且y=+1,则:ω=ω+X,b=b+1;
(3)再取另一个训练样本(X,y),重复步骤(2);
(4)终止条件:直到所有训练样本(X,y)均不满足(2)中的所有条件。
三、感知机的求解过程的步骤(2)的解释
(1)当ω训练样本(X,y)满足ωTX+b>0,且y=-1时,该训练样本未达到平衡状态,需通过ω(新)=ω(旧)-X,b(新)=b(旧)-1的方式调整。通过上述方式调整后:
ω(新)TX+b(新)
=[ω(旧)-X]TX+b(旧)-1
=[ω(旧)TX+b(旧)]-(XTX+1)
=[ω(旧)TX+b(旧)]-(||X||2+1)
≤[ω(旧)TX+b(旧)]-1
即通过调整后,新ωTX+b值比旧ωTX+b值至少小1,在旧值的基础上向平衡状态方向移动。
(2)当ω训练样本(X,y)满足ωTX+b<0,且y=+1时,该训练样本未达到平衡状态,需通过ω(新)=ω(旧)+X,b(新)=b(旧)+1的方式调整。通过上述方式调整后:
ω(新)TX+b(新)
=[ω(旧)+X]TX+b(旧)-1
=[ω(旧)TX+b(旧)]+(XTX+1)
=[ω(旧)TX+b(旧)]+(||X||2+1)
≥[ω(旧)TX+b(旧)]+1
即通过调整后,新ωTX+b值比旧ωTX+b值至少大1,在旧值的基础上向平衡状态方向移动。
编辑:黄飞
-
人工神经网络原理及下载2008-06-19 9721
-
神经网络教程(李亚非)2012-03-20 56638
-
人工神经网络课件2016-06-19 6376
-
人工神经网络算法的学习方法与应用实例(pdf彩版)2018-10-23 9352
-
【专辑精选】人工智能之神经网络教程与资料2019-05-07 3773
-
机器学习神经网络参数的代价函数2019-05-22 1730
-
人工神经网络实现方法有哪些?2019-08-01 3422
-
【AI学习】第3篇--人工神经网络2020-11-05 4117
-
如何用卷积神经网络方法去解决机器监督学习下面的分类问题?2021-06-16 2912
-
卷积神经网络模型发展及应用2022-08-02 13207
-
卷积神经网络简介:什么是机器学习?2023-02-23 25379
-
不可错过!人工神经网络算法、PID算法、Python人工智能学习等资料包分享(附源代码)2023-09-13 3958
-
卷积神经网络算法是机器算法吗2023-08-21 1398
-
人工神经网络模型包含哪些层次2024-07-05 2246
-
人工神经网络的原理和多种神经网络架构方法2025-01-09 2384
全部0条评论

快来发表一下你的评论吧 !

