谐振式电源的基本原理 谐振开关的动态过程分析

电路的谐振现象

为了更好地理解谐振式电源，这里回忆一下电路谐振的条件及其特点。

一、串联电路的谐振

一个R、L、C串联电路，在正弦电压作用下，其复阻抗：

Z=R+j(ωL-1/ωC)

一定条件下，使得XL=XC，即ωL=1/ωC ，Z=R，此时的电路状态称为串联谐振。

明显地，串联谐振的特点是：

1．阻抗角等于零，电路呈纯电阻性，因而电路端电压U和电流I同相。

2．此时的阻抗最小，电路电流有效值达到最大。

3．谐振频率：ωo=1/√LC 。

4．谐振系数或品质因素：

Q=ωoL/R=1/ωoCR=（√L/C）/R。

由于串联谐振时，L、C电压彼此抵消，因此也称为电压谐振。从外部看，L、C部分类似于短路。

而此时Uc、UL是输入电压U的Q倍。Q值越大，振荡越强。

这里的Z0=√L/C，我们称为特性阻抗，它决定了谐振的强度。

5．谐振发生时，C、L中的能量不断互相转换，二者之间反复进行充放电过程，形成正弦波振荡。

二、并联电路的谐振

一个R、L、C并联电路，在正弦电压作用下，其复导纳：

Y=1/R-j(1/ωL-ωC)

一定条件下，使得YL=YC，即1/ωL=ωC ，Y=1/R，此时的电路状态称为并联谐振。

明显地，串并谐振的特点是：

1．导纳角等于零，电路呈纯电阻性，因而电路端电压U和电流I同相。

2．此时的导纳最小，电路电流有效值达到最小。

3．谐振频率：ωo=1/√LC 。

4．由于并联谐振时，L、C电流彼此抵消，因此也称为电流谐振。从外部看，L、C部分类似于开路，L、C各自有效电流却达到最大。

5．谐振发生时，C、L中的能量不断互相转换，二者之间反复进行充放电过程，形成正弦波振荡。

谐振式电源的基本原理

谐振式电源是新型开关电源的发展方向。它利用谐振电路产生正弦波，在正弦波过零时切换开关管，从而大大提高了开关管的控制能力，并减小了电源体积。同时，也使得电源谐波成分大为降低。另外，电源频率得到大幅度提高。PWM一般只能达到几百K，但谐振开关电源可以达到1M以上。

普通传统的开关电源功率因素在0.4-0.7，谐振式电源结合功率因素校正技术，功率因素可以达到0.95以上，甚至接近于1。从而大大抑制了对电网的污染。

这种开关电源又分为：

1．ZCS——零电流开关。开关管在零电流时关断。

2．ZVS——零电压开关。开关管在零电压时关断。

在脉冲调制电路中，加入L、C谐振电路，使得流过开关的电流及管子两端的压降为准正弦波。下面是这两种开关的简单原理图。

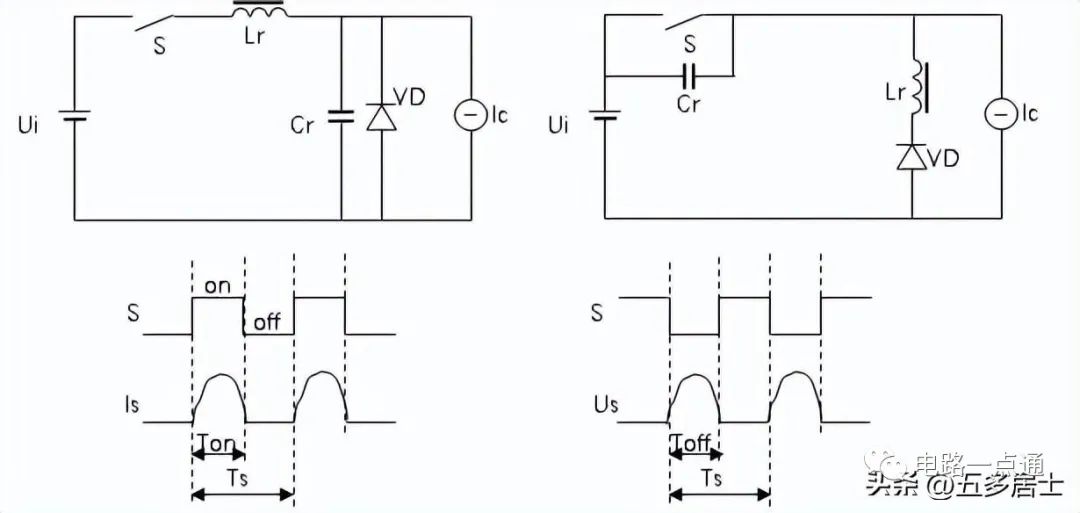
图1：电流谐振式开关电路 电压谐振式开关电路

ZCS电流谐振开关中，Lr、Cr构成的谐振电路通过Lr的谐振电流通过S，我们可以控制开关在电流过零时进行切换。这个谐振电路的电流是正弦波，而Us为矩形波电压。

ZVS电压谐振开关中，Lr、Cr构成的谐振电路的Cr端谐振电压并联到S，我们可以控制开关在电压过零时进行切换。这个谐振电路的电压是正弦波，而Is接近矩形波。

以上两种电路，由于开关切换时，电流、电压重叠区很小，所以切换功率也很小。

以上开关电源是半波的，当然也可以设计成全波的。所以又有半波谐振开关和全波谐振开关的区分。

谐振开关的动态过程分析

实际上，谐振开关中的所谓“谐振”并不是真正理论上的谐振，而是L、C电路在送电瞬间产生的一个阻尼振荡过程。下面，我们对这个过程做一些分析，以了解谐振开关的工作原理。

一、零电流开关

实际的零电流开关谐振部分拓补又分L型和M型。如下面两组图形所示：

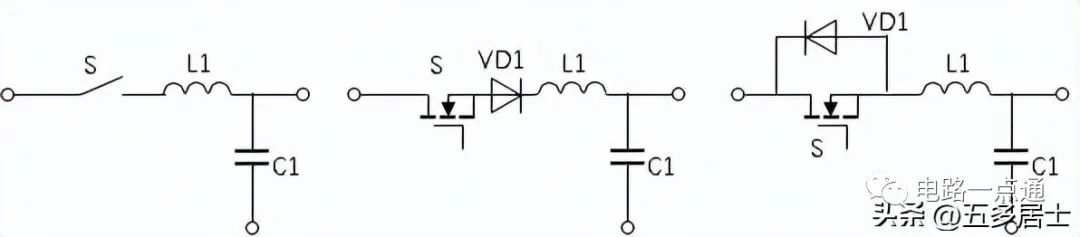
图2：L型零电流谐振开关（中半波，右全波）

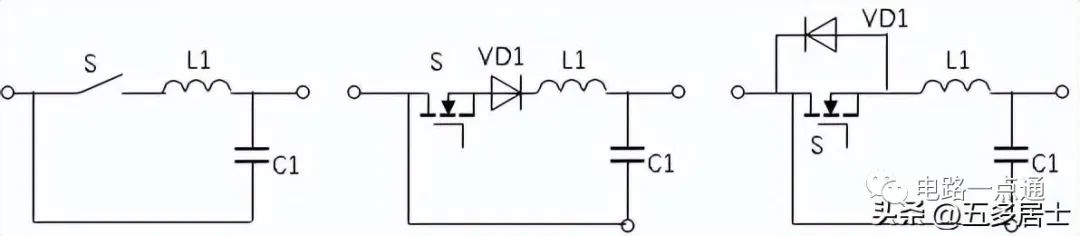
图3：M型零电流谐振开关（中半波，右全波）

这里的L1用于限制di/dt，C1用于传输能量，在开关导通时，构成串联谐振。用零电流开关替代PWM电路的半导体开关，可以组成谐振式变换器电路。按照Buck电路的拓补结果，可以得到如下电路：

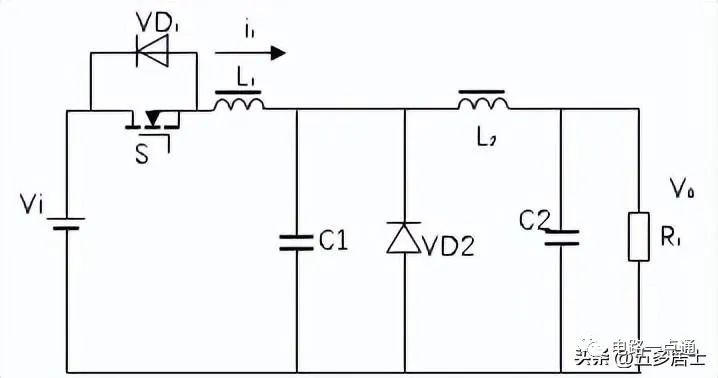
图4：Buck型准谐振ZCS变换器（L型）

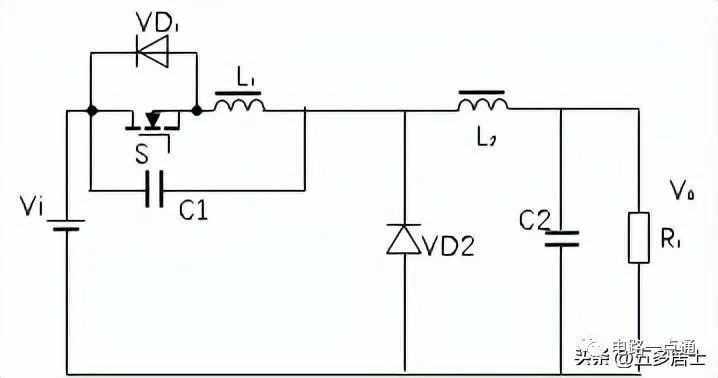
图5：Buck型准谐振ZCS变换器（M型）

这里，我们分析一下L型电路的工作过程。

假定这是一个理想器件组成的电源。L2远大于L1，从L2左侧看，可以认为流过L2、C2、RL的输出电流是一个恒流源，电流I0。谐振角频率：

ω0=1/√L1C1 。

特性阻抗：

Z0 =√L1/C1）。

动态过程如下：

1．线性阶段（t0-t1）：

在S导通前，VD2处于续流阶段。此时VVD2=VC1=0。S导通时，L1电流由0开始上升，由于续流没有结束，此时初始VL1=Vi。

由VL1=Vi=L1di/dt，且L1初始电流为0，有：

i1=Vi(t-t0)/L1
----------------------------------式1

到t1时刻，达到负载电流I0，因此：

此阶段持续时间：

T1=t1-t0=L1I0/Vi

由式1，可以看出，此阶段i1是时间的线性函数。

2．谐振阶段（t1-t2）：

在电流i1上升期间，当i1小于I0时，由于i1无法供应恒流I0，续流过程将维持。当i1=I0时，将以i1-I0对C1充电，VD2开始承受正压，VD2电流下降并截止。L1、C1开始串联谐振，i1 因谐振继续上升。

iC1=C1dVC1/dt=i1-I0

VL1=L1di1/dt=Vi-VC1

因而：

i1=I0+ iC1=I0+Vi/Z0*sinω0 (t-t1)------------------式2

其中，iC1为谐振电流。

VC1=Vi-VL1= Vi -Vicosω0 (t-t1)= Vi [1-icosω0 (t-t1)]--式3

谐振到ta时刻，谐振电流归零。如为半波开关，则开关自行关断；如果是全波开关，开关关断后，将通过VD1进行阻尼振荡，将电容能量馈送回电源，到时刻tb电流第二次为0。本阶段结束，这时的时刻为t2。

VC1在i1谐振半个周期，i1=I0时，达最大值。i1第一次过零（ta）时，S断开。如为半波开关，则谐振阶段结束。如为全波开关，C1经半个周期的阻尼振荡到电流为0（tb）时，将放电到一个较小值。

从式2、3，可以看出谐振阶段ta前，i1、VC1是时间的正弦函数；如为全波开关，还有一段时间的阻尼振荡波。

3．恢复阶段（t2-t3）：

由于VC1滞后1/4个谐振周期，因而在t2后，因L2的作用还将继续向负载放电，直至VC1=0。这阶段，如考虑电流方向性：

I0=-C1dVC1/dt

故：VC1= VC1（t2）-I0（t-t2）/C1
------------------------------------式4

因此，这个阶段的VC1是时间的线性函数，电压从VC1（t2）逐步下降到零。如为半波开关，则开关分压也将线性上升到输入电源值。

4．续流阶段（t3-t4）：

当电容放电到零后，VD2因反压消失而导通，对L2及负载进行续流，以保持电流I0连续。

此时，我们可以根据电路的要求，选择在适当时间再次开通S，重新开始线性阶段。

根据以上导出的各公式，可以得到如下的波形图：

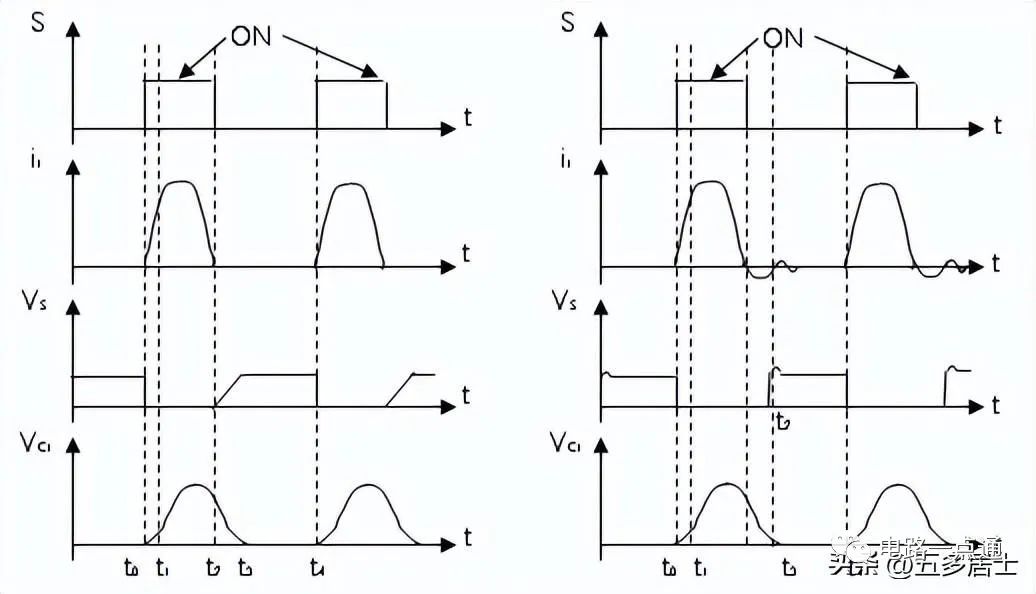
图2-18：半波ZCS开关波形 全波ZCS开关波形

从以上分析可以看出，ZCS谐振开关变换器的开关管总是在电流为0时进行切换。

实际情况与理想分析有所不同，VC1将有所超前。

M型电路分析方法类似，不再赘述。

二、零电压开关

ZCS在S导通时谐振，而ZVS则在S截止时谐振，二者形成对偶关系。分析过程大体类似，此处从略。

综合以上分析过程，我们可以看出，该拓补谐振结构只能实现PFM调节，而无法实现PWM。原因是脉冲宽度仅受谐振参数控制。要实现PWM，还需要增加辅助开关管。

审核编辑：汤梓红