量子磁性有谱么⸺有SU(3)中子散射谱

老生常谈，凝聚态物理的基本任务之一，就是构建材料结构与物理效应间的内在联系。这里的结构，包括晶体结构、电子结构和介观微结构 (如畴) 等。时至今日，为达此目的，物理人长期探索，积累了成系统的结构表征方法。其中广泛应用的方法应属散射谱学，覆盖从光 / 声波谱、到电子散射、再到中子散射和 X 射线散射等大类，另有诸多小类不提。其中每一类技术，依然在不断更新、拓展，以追求更快、更细、更强。这里，需要提及，虽然波的“衍射 (diffraction)”和“散射 (scattering)”从本源定义上有所不同 (衍射更多与波的属性相联系)，但从材料与波相互作用角度，不妨将衍射归属于散射之一类，用“散射”统达。

在学生时代，Ising 学习使用光学显微术和 XRD 时，并不十分理解散射表征的物理和内在机缘，只是被动从老师那里学习如何使用和知其然。一般材料人，也不过是从布拉格定理那里理解 XRD 原理：晶体结构之某一晶面满足 2d‧sin(θ) = nλ，就有相干增强的衍射而出，形成衍射峰。后来，又接触诸如劳埃斑图、ϕ 扫描、单晶极图等衍射技术。得益于老友杨平博士指点，Ising 作为用户也算是走到左右开弓、熟能生巧 XRD 的大门外了。不过，即使如此，那时候还是很少去理解散射谱的博大精深，更别提散射测量乃非破坏表征技术这一优点。

由此，基于前人积累的计算或表征结果，基于对晶体结构与原子占位的初步认知，我们从 XRD 测量原则上能解构出材料微结构的一些信息，如结晶度、取向、晶粒大小、单晶与否和晶格畸变大小等。这里的结构信息是静态的，尚无法得出结构动力学的信息，如晶格振动、电荷转移跃迁、自旋激发转换等。XRD 也因此与常见的红外 / 拉曼 (IR / Raman)、光电子能谱等散射谱学方法不同。前者呈现的只是散射强度与波矢的关系；后者则携带了能量交换转移的信息、具有动力学特征，因此是功能更强大、广谱和更有价值的散射方法。

当然,话虽如此，非行家尚不能深刻理解其中门道。二十年前，为了糊口，Ising 开始接触量子材料，就读到十八般表征武学中以散射表征最为广博常见。到今天，已有了粗浅感受：散射谱学 (scatteringspectroscopy)，如果将电子显微术也算上，毫无疑问是量子材料人“表征”和“理解”结构 - 效应关系的主体方法。从长波到 X 射线各种波源，从电子电荷、自旋、轨道到晶格畸变与声子模等散射结构自由度，各类谱学相互对接、对应、佐证，虽不能说全域覆盖而面面俱到，但也构筑了材料表征的主干与最大群体。

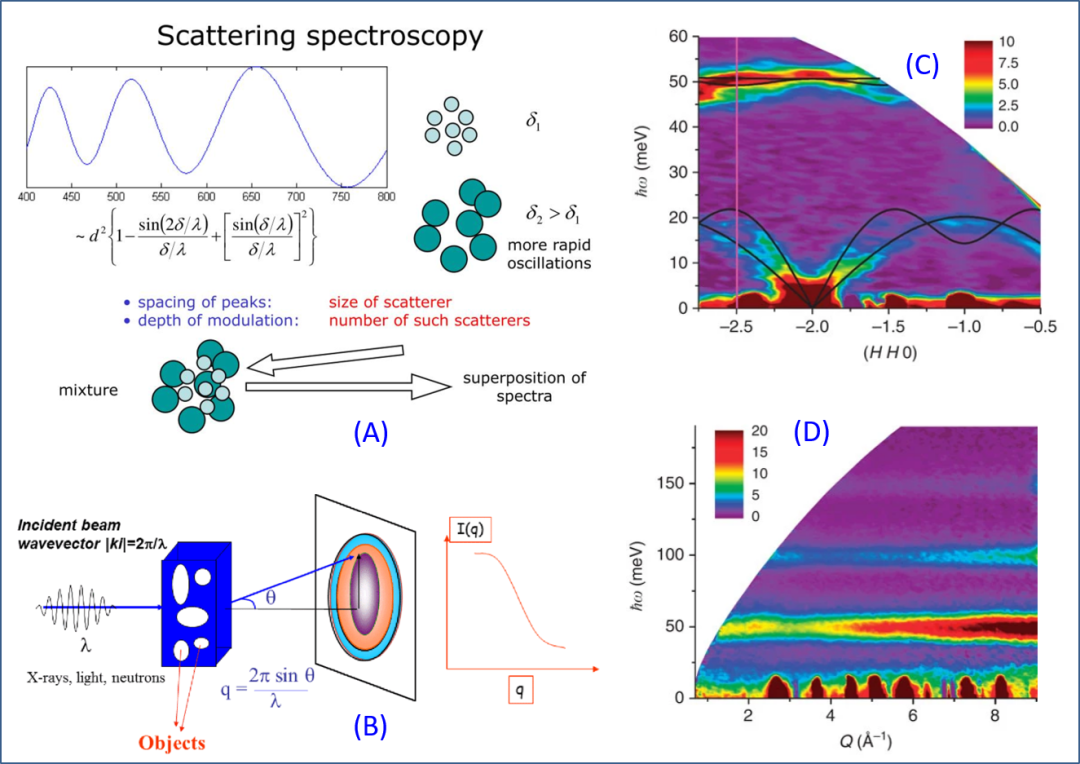
图 1.(A) & (B) 凝聚态物质对波的散射谱学之直观表达：散射强度 I 与波矢 q (或 k) 的关系 I(q / k)，更多则表达为散射强度与波矢 (q)和波动能量 (E = hω) 的两维关系 I(q, ω)。后者通常称之为动力学散射谱。作为散射谱的示例，(C) & (D) 显示化合物 UN 的非弹性中子散射谱 (Inelastic neutron scattering data from compoundUN measured at SEQUOIA for T = 5 K)。特别值得指出，在图 (C) 中，那些位于高散射强度附近的低能标物理，很可能因为存在寿命短和能量低而淹没于高强度主峰的背景中，难以提取！

图 1 以简单的方式展示了散射谱学的一些初级物理。这里需提及两个名词：“表征”、“理解”。前者乃表达客观实验探测，后者乃表达主观理论计算，它们是“散射谱学”这枚物理品牌的两面，不可或缺。为了好的“表征”，除技术提升和更新本身，需要有一些关于材料结构的基本认知，以便选择测量方法和参数条件。相关详细内涵，读者可参见相关专著和教程。而为了好的“理解”，存在两个互为因果的环节：

(1) 正向理解，指从前人的研究结果中得出结构的基本认知，由此去理解散射谱包含的新信息。不妨以拉曼散射探测结构畸变为例来说明。假定材料的结构及其拉曼散射模式已知，如果测到的拉曼谱偏离标准谱或出现新的散射模式，就可从结构畸变角度去理解偏离所蕴含的新效应。

(2) 反向理解，指对材料的结构几无所知，完全依赖从散射谱倒推结构。这样的操作可能是散射谱学最精彩和独特之处，从而让物理人着迷及废寝忘食。通常的做法是通过类比和经验，假设结构模型，包括第一性原理计算推演结构及动力学，将预测的散射谱与实验测量进行细致比对。如此多重反馈，以求达到计算与实验的契合。

如上所言，说起来容易，但真要很好实施，还是有难度的。要满足量子材料的需要，难度会更大。为了说明之，需对散射谱学的主干与脉络有所了解。如图 1(B) 所示，散射谱学的基本内涵可能包括：

(1) 首先，它立足于波与物质相互作用。特定波长 λ (或频率 ω) 的波，入射到样品内，经历散射后的波信号 (依赖波矢 q / k)，携带了材料内不同尺度结构 (如原子核、电子、晶格和畴) 激发的动量 (k) 与能量 (E = hω)信息。此乃所谓“表征”的原理，其信息含有动力学特征。

(2) 其次，除非是那种超高精度的 focused 会聚波束，一般散射谱信号覆盖了样品足够大区域，散射来自大数粒子集合或宏观整体行为。因此，散射谱学反映的是 collective 模式的物理，贴合凝聚态物理致力于大数粒子集体行为研究的本质特征，为建立结构 – 效应之间的关系搭建了更直接的“表征”桥梁。

(3) 过去数十年，甚至两百年，物理人围绕散射表征已建立起五花八门的方法。一个例子是图 1(C) & 1(D) 所示例的、针对“氮化铀 UN”的非弹性中子散射谱 (Inelasticneutron scattering data from compound UN measured at SEQUOIA for T = 5 K)。由图可见，现在可得到的散射谱，称得上是美轮美奂，就如江山瑰丽、催人探寻。

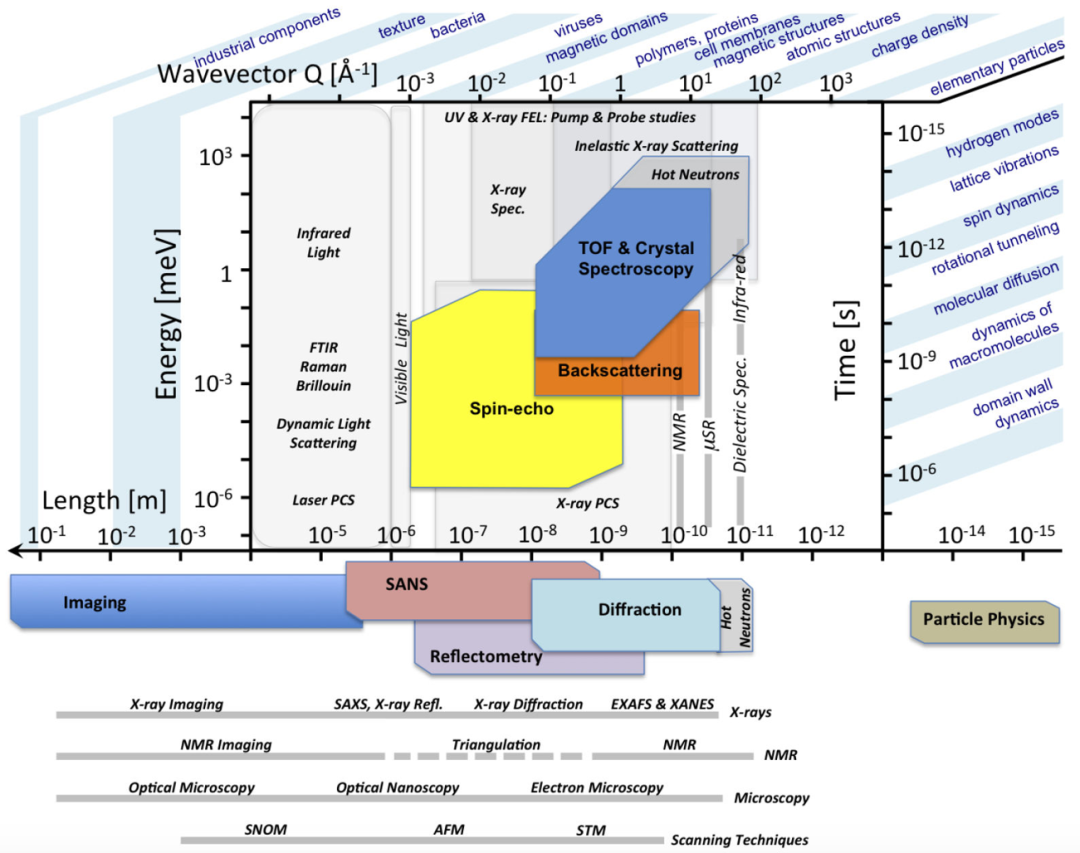
图 2. 欧洲散裂光源 (The European Spallation Source) 绘制的中子散射谱物理与应用领域。这幅图足够我们仔细学习揣摩一周，并激发更多新的物理新谱。

实现如上内涵，硬件平台技术是前提。图 2 给出了欧洲散裂源 (The EuropeanSpallation Source) 绘制的散射物理与应用集成图，令人印象深刻，虽然不限于凝聚态！对其中所展示的各种技术之原理和细节，这里无法一一描绘，读者可参考相关专著。本文姑且写写“理解”散射谱的读书笔记，特别是针对结构及动力学未知的情况。对传统或经典材料，Ising 学到一些皮毛知识：

(1) 对一新体系，确定化学组成之后，用 XRD 和中子衍射等技术解构其晶体结构，已经不是难事。有了晶体结构，就有了解构散射谱的基础。植入晶格对称性的知识，物理人从第一性原理出发，对电子结构、声子结构等决定散射谱的主要要素做出初步描绘，应算水到渠成。这是凝聚态中大能标物理，所涉及的问题是经典材料学的主题。

(2) 基于这些 (晶格、电子、声子) 初步知识，利用诸如红外、拉曼、光电子、同步辐射、中子等散射谱学方法，能够得到与材料化学键合、声子振动、载流子激发、自旋涨落等有关的谱学信息。将这些信息与计算预测的散射谱进行比较对照，通过精修而最终达到准确和全面理解材料结构。

行文至此，依稀感觉到散射谱解谱的环节：如何从已有的零星结构知识去计算预测散射谱？对散射谱的解谱，事实上也已形成相对专门化的理论和计算方法 (软件包)。而且，这些方法也在变得复杂、细致。不过，最基本的物理，依然是求解参与波散射的那些结构自由度之间的关联函数或结构因子 (correlationfunction or dynamical structure factor)。众所周知，特定的散射，对应于特定的结构自由度。例如，中子散射，特别适合提取自旋相关的散射，对应地需要计算自旋结构因子 (spin structurefactor)。再例如，光散射，可提取晶格声子层面的散射，对应地就需要计算声子相关的结构因子。以自旋结构的中子散射为例来说明结构因子计算：如果已知自旋结构 (即磁结构)，就能写出自旋对中子束的散射截面 (自旋散射因子)。然后，将所有自旋散射截面 (scatteringcross-sections) 叠加起来，就是常说的结构因子。这一结构因子与测量得到的散射谱有正比关系，构建了计算与测量结果之间反复比对精修的基础。

好吧，在如上散射谱解谱的框架下，物理人面临的问题是：(A) 您怎么能知道自旋结构？(B) 自旋结构如果出现时空涨落演化，散射谱又是如何模样？如果这样的结构自由度由大能标相互作用决定，如晶格构型、电荷有序相、自旋有序相、声子模等，粗略的第一性原理计算或唯象理论预测，大致可以“八九不离十”地接近真相。其中道理，无非是能标大了，对应的结构将一家独大，那些难以被考量的不准确性和实验误差，难以撼动这一家独大！

问题是，到了量子材料那里，情况可能就不同了。量子材料感兴趣的结构自由度与对应的效应，大多由能标为 ~ meV 的相互作用所决定。此时，计算预测的不准确性、实验条件限制、各种实验误差等，就足以严重扭曲变形所得到的散射谱，也就扭曲了对所追求的本征结构自由度及其动力学的“理解”。

不妨以“量子磁性”为例来述说一二，以展示散射谱所面对的问题。所谓量子磁性，Ising 狭隘理解是指那些高度磁阻挫的体系。它们或许是缺乏长程序的自旋纠缠态 (如量子自旋液体)，或许有多个自旋简并态，或许会展现量子涨落等引发的诸多低能磁激发。这些激发包括自旋波 / 涡旋激发、磁振子等低能磁激发态，展现出强烈量子特征，也就是低能标物理。由此，马上就可提出若干令人抓狂的疑虑：

(1) 需要用量子理论去处理量子磁性自由度及其动力学？量子磁性的哈密顿求解，其计算量与自旋数目呈现指数发散关系，大尺度的磁性问题必然难倒牛人一片。事实上，即便是有可能将量子磁性问题近似成经典哈密顿模型，其求解计算量与自旋数目也大致成正比关系。这个正比关系已经让多少物理人白了少年头，而指数关系则干脆就是鸿沟无限、难于上青天、难住 99.99 % 的物理人。到头来，剩下那 1 %% 的人们，不得不去思考有什么解决之道！时至今日，结果依然不那么乐观，似乎机器学习和 Chat GPT 也不行。

(2) 需要探测的是自旋自由度的散射，散射谱应包含了自旋位置和取向两个变量的信息，对非共线自旋结构殊为重要。众所周知，非共线磁结构，是包括散射谱学在内的磁结构探测技术的硬骨头，其中难处一言难尽^_^。

(3) 无论是基于应用，还是基于基础探索，拓展到宽温区和高温区总是必要的。一个量子磁性体系，其量子涨落问题不能忽视。而到了高温区，其经典热涨落效应会更显著、更难处。

总之，量子磁性问题涉及的能标小，给散射谱学“理解”其中磁结构及动力学带来挑战。当然，即便是充满挑战，依然会有量子材料人偏向虎山行、取得进展。

审核编辑：刘清