AI芯片上利用Poly进行软硬件优化的一些问题

1. 关于IR

我们在这篇文章中主要关注的是Poly的IR。在之前的内容中，我们主要基于Poly传统的schedule tree表示介绍了如何实现AI芯片上的软硬件优化。Google MLIR[29]针对schedule tree的不足，提出了一种简化的Poly IR。以图22中所示的代码为例，用schedule tree对该部分代码进行表示，可以得到如图23所示的IR形式，而MLIR则是将其表示成图24的形式。（注：图23中的schedule tree与图18-21表示的内容一样，只不过这里用文字的形式表示出图的内容，图23中schedule后的标量维度可以对应为图18-21中的sequence节点。）

图22 另一个简单用例

图23 图22代码的scheduletree表示

图24MLIR对图22中的简化Poly IR

通过对比可以看出，MLIR的Poly IR对循环进行了更加显式的表达，而省略了schedule tree中的domain、schedule等信息。这种Poly IR简化了Poly在实现循环变换之后的代码生成过程。例如，在实现倾斜变换时，MLIR可以直接基于图24生成如图25所示的Poly IR。

图25 经过倾斜后的MLIR的Poly IR

但是相比于传统的schedule tree表示，循环变换的过程更复杂了。在schedule tree上，循环变换，如这里的倾斜，可以直接修改schedule的仿射函数来实现，可参考图6；但在MLIR中却要对应地修改显式表达的循环变量及对应的下标信息。

笔者对这种方案存在两点疑问。一是在Poly的整个流程中，虽然代码生成也比较复杂，但是循环变换的时间开销可能比代码生成的开销更高，虽然简化了代码生成，但是循环变换更加复杂，不知道这样的代价是否值当？当然，Google MLIR团队集结了编译领域最顶级的专家和最熟悉Poly的研究团队，笔者相信他们提出这种简化的Poly IR肯定是经过深思熟虑的，可能后期需要向Google MLIR的Poly专家再请教之后才可能解答这个疑惑。二是这种简化的Poly IR是为了简化从ML Function到CFGFunction的代码生成过程，那如果Poly变换之后的输出不是基于LLVM IR的框架是否还有必要采用这种简化的Poly IR？毕竟，目前深度学习框架的“IR之争”还没有结束。

2. 关于循环变换

Poly的调度算法[19-22]基于线性整数规划来求解新的调度仿射函数，而这个过程中会考虑到几乎所有的循环变换及多个循环变换之间的组合。以图26[30]为例是线性整数规划问题求解的示意图，其中蓝色的点表示整个空间上的整数，而图中的斜边可以看作是循环边界等信息给出的约束，这些约束构成了一个可行解区间（图中绿色部分）。那么调度问题可以抽象成在这个绿色的解空间内寻找一个目标问题（红色箭头）的最优解（在Poly 里，就是寻找按字典序最小的整数解）。

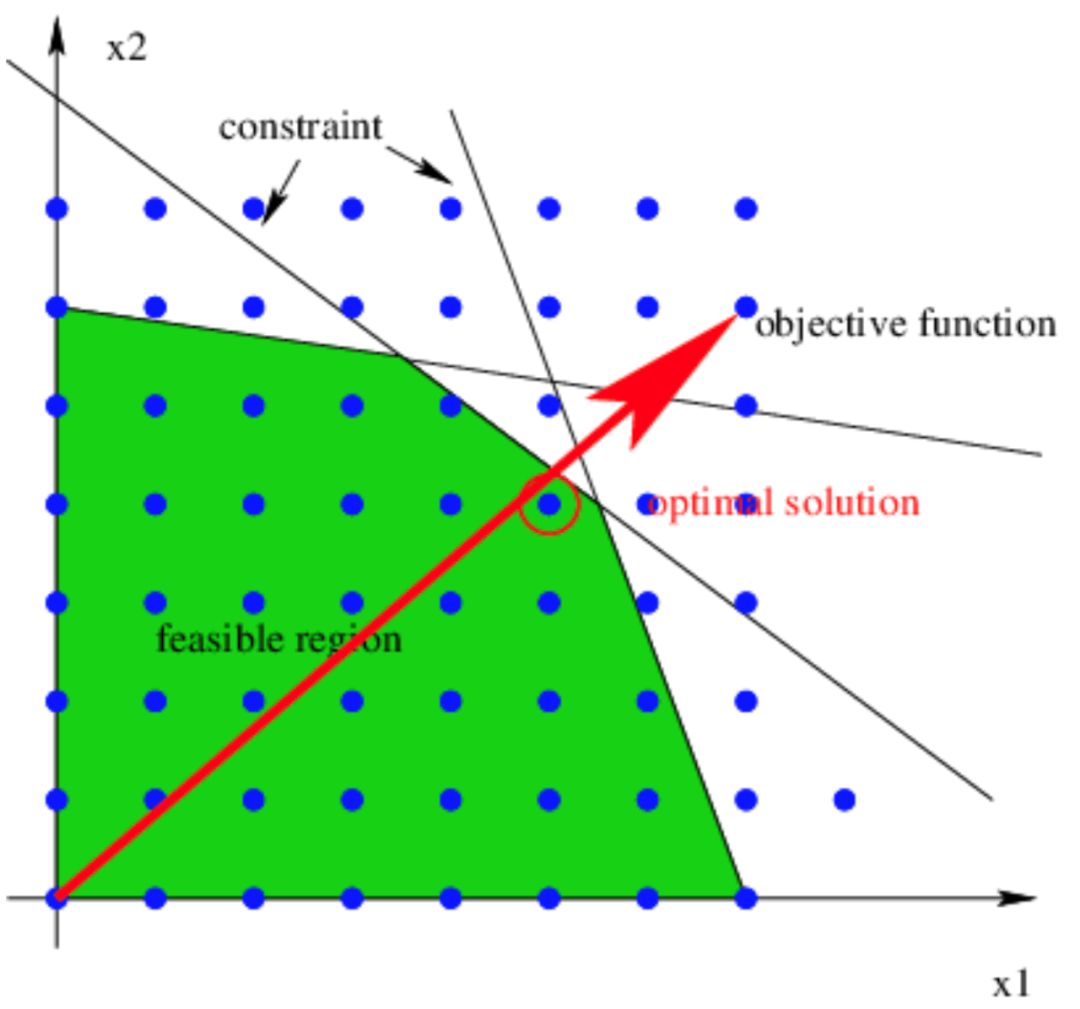
图26 线性整数规划问题示意图

但是，一个重要的前提条件是Poly是面向通用程序设计语言的编译数学模型，如果我们将Poly应用到如深度学习这样的特定领域，是否需要考虑和通用语言一样的循环变换集合？一个很简单的例子是对于一个卷积算子，卷积核的循环嵌套会嵌套在输入图像的循环嵌套内部，而卷积核的循环维度范围可能会比输入图像的循环维度范围小很多。当Poly计算新的调度时，输入图像的循环维度和卷积核的循环维度可能发生倾斜变换，但这种倾斜似乎对卷积计算后面的变形、代码生成等问题都不太友好。所以，Poly调度算法考虑的循环变换，在深度学习领域是否都需要，还是只需要比较核心的、对性能提升比较关键的几种变换？如果我们减少了需要考虑的循环变换个数及其组合，也就是说在图26中我们缩小了可行解的区间，那么求解起来是不是会更高效一些？

如果上面问题的答案是肯定的，那么笔者认为目前而言Poly能实现的循环变换中，对深度学习应用最关键的循环变换应该是分块和合并（可能有待商榷）。假设只考虑分块和合并这两种循环变换，这种情况下问题似乎简单一些。但是编译优化中还有一个比较关键的问题就是如何决定实现的循环变换的顺序。是先做合并后做分块，还是先做分块再做合并？事实上，对于循环变换的顺序判定问题，传统的Poly中间表示没有给出明确的答案，而不幸的是，MLIR也没有解决这个问题。当然，这只是极简情况下的假设。只有分块和合并显然是不够的，因为循环变换后的代码生成还要借助distribution（分布）来保证向量化等问题的发掘。

3. 关于分块

我们前面针对GPU、TPU以及昇腾910的架构都进行了分析，（多级）缓存是目前市场上AI芯片采用的架构趋势，而专用AI芯片如TPU、昇腾910等专用计算单元的设计似乎也引领了AI芯片的另一种方向。可以说，在当前的AI芯片上，分块是软件栈必须实现的一种优化手段了。

而针对分块这一种变换而言，仍然还有很多值得研究的问题。比如，以图27[31]中的二维卷积为例，卷积核（kernel）通过在输入图像（input）上进行“滑动”来计算输出图像（output）的结果。当卷积核针对输入图像的某一个像素点（图中深蓝色的方块）进行计算时，需要通过对其周边特定区域的像素点（图中浅蓝色的方块）进行加权（即卷积操作）后得到输出图像上的一个像素点（图中红色方块）。由于卷积核需要在输入图像上进行滑动，这种滑动的过程在大多数情况下会导致输入图像的数据被多次访问。以图27为例，当滑动的步长（stride）为1时，除输入图像上第一列和最后一列的像素点之外所有的像素点都会被重复计算。如果我们按照卷积核的大小对输入图像进行分块，那么分块之后输入图像的每个分块之间都会存在overlap（数据重叠）问题。如何利用Poly在深度学习应用中自动实现这种满足数据重叠的分块？

图27 卷积操作示例

一种方式是采用PolyMage[6]类似的方法利用Poly的调度来求解这样的overlap的区间，但是这种方式有可能会导致过多的冗余计算，而且用调度来求解分块的形状在某种程度上会使Poly的过程变得更加复杂，代码生成亦如是；另一种方式是在schedule tree上利用特殊的节点来实现，但是目前这种方式的代码实现都还没有公开。

另外一个问题是在上一期的内容中有读者提问到关于分块和冗余计算的问题。冗余计算的确会给性能的提升带来一定的影响，但是这种冗余计算的引入是为了实现分块之间的并行。我们在前文提到过，并行性和局部性有的时候是冲突的，为了达到两者之间的平衡，往往是需要作出一些其它的牺牲来达到目的[32]。而更重要的是，这种带有冗余计算的分块形状是目前几种分块形状中，实现降低内存开销最有效的一种形状。以图28[6]为例，图中列出来三种不同的分块形状，其中最左侧的梯形分块引入了冗余计算，但是这种分块在一次分块计算完成（水平方向）后，分块内需要传递给下一次计算的活跃变量（红色圆圈）总数最少，而其它形状如中间的分裂分块和最右侧的平行四边形分块剩余的活跃变量总数都很多，无法实现有效降低内存开销的目的。（注：图中未分析钻石分块[25]和六角形分块[26]，但是这两种分块可以看作是分裂分块的一种特殊形式。）

图28 不同分块形状分块内活跃变量的分析对比

除此之外，分块面临的问题还有很多。比如，Poly中实现的分块都是计算的分块，而数据分块只是通过计算分块和计算与数据之间的仿射函数来计算得到，这种结果能够保证数据的分块是最优的吗？在分布式结构上呢？而针对TPU和昇腾910等专用AI加速芯片，多级分块应该如何实现才能更好的发挥这些加速芯片的特征呢？

4. 关于合并

循环的合并是一个挖掘局部性的过程。我们仍然想强调的问题是，局部性和并行性是加速芯片上两个非常重要的变换目标，但是这两个目标有的时候是互斥的，就如我们在图10和图11中所示的例子一样。合并的循环越多，破坏计算并行性的可能性越大；而如果要保持计算的并行性，可能就要放弃一些循环的合并。

然而，在不同的架构上哪些合并是最优的，似乎静态判定是不太可能的。就如我们在第一部分分享的那样，在CPU上生成OpenMP代码可能一层并行就足矣，这时局部性的效果可能就比并行性的效果更好；而在GPU上，由于有两层并行硬件的抽象，可能并行性的收益比局部性的效果更佳。所以，现在许多深度学习软件栈也采用了Auto-tuning的方式来通过实际的多次运行来判定哪种策略是最优的。然而，即便是Auto-tuning的方式，能够保证遍历到所有的合并形式吗？如何选择一个合适的合并策略，是必须要通过调优的方式来确定吗？利用静态分析的方式来遍历所有合并策略的工作也研究过[33]，但是这种动态规划的方式是不是又会带来时间复杂度的问题？

5. 关于Poly时间复杂度和对Poly的扩展

关于Poly的时间复杂度问题，我们在上文中已经提到Poly的调度实质是线性整数规划问题的求解过程，而实际上Poly的代码生成过程也会涉及到线性整数规划问题的求解。我们在讨论深度学习领域是否需要所有的循环变换及其组合的时候，设想从减少循环变换的个数来减小解空间，以此来加速调度的过程；另外，MLIR的初衷也是为了降低代码生成的复杂度。而文献[34, 35]也试图对特定情况或者将线性整数规划问题简化为线性规划问题来降低时间复杂度。不过，诸此种种都没有从实质上解决掉问题的关键，因为问题的实质仍然是NP级别的难题。想要从质上改变这个现状，可能还需要一段比较长的时间，其它的计算机科学领域的方法比如constraint programming说不定也能是一个解决的方法。

另外，Poly的静态仿射约束对稀疏tensor等领域的扩展也提出了挑战。关于稀疏tensor的工作目前也有了一定的研究[36, 37]，但Poly无法直接应用于含有非规则下标的tensor的情况，怎么样在这个领域对Poly进行扩展也可能是深度学习利用Poly优化的另一个需要解决的问题。因为Poly在解决稀疏矩阵问题的研究时，有了一定的进展[38-41]，这说明Poly的non-affine扩展还是可行的，而深度学习框架的可定制性给这个问题也创造了更多的机会。