

电机轴承外圈蠕变的不同机理
工业控制
描述
轴承蠕变的研究在20世界50年代就已经开始,并形成了系列蠕变理论,有些理论一直沿用至今。轴承蠕变是指在轴承配合面之间相对发生滑动,分为内圈蠕变和外圈蠕变。 电机轴承蠕变引起的最常见失效模式是机壳轴承座磨损产生铁屑,产生的后果轻则影响NVH,重则影响系统高压绝缘/轴承损坏 ,因此电机轴承蠕变专题主要讨论的是电机轴承外圈蠕变。
(一)
电机轴承通常采用深沟球滚动轴承,轴承外圈与壳体之间的配合是间隙,轴承内圈与转轴之间的配合是过盈。电机轴承工作环境可以参考下图中的奥迪E-TRON剖视图。

前面谈到轴承蠕变是指在轴承配合面之间相对发生滑动,有两种情况:一种是轴承外圈与内圈旋转方向相同,另外一种则是轴承外圈与内圈旋转方向相反。
1. 反向旋转蠕变
N. Soda在1964年指出了两种反向旋转轴承蠕变机理。 其中一种是众所周知的,由于轴承外圈与轴承座间隙引起的蠕变 。当旋转载荷作用在轴承上时,如果装配表面与环之间的间隙为c,则轴承每旋转一周时,轴承外圈会延迟πc,从而导致与转轴旋转方向相反的蠕变。
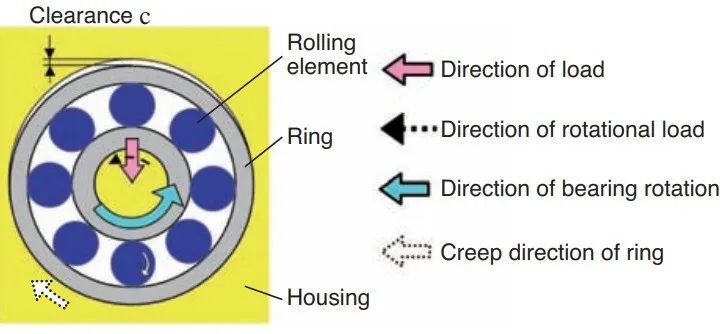
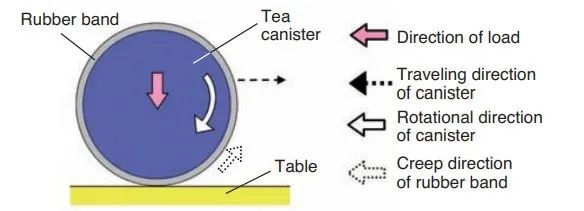
另一种是由于无间隙时轴承外圈的弹性变形和滑动引起的 。研究者以带橡皮筋的塑料罐来做说明:由于橡皮筋和茶叶罐之间的小滑动,在低于负载的某个点处,随着塑料罐滚动,其向前累积。
起初,橡皮筋会因茶罐的负荷而变形,并沿圆周方向伸展。这种变形是对称的,左右之间的滑动也相同,因此,不应发生向一个方向移动的蠕变。但是,当茶叶罐滚动时,由先前的滑移引起的变形仍然保留,导致不对称。随着向一个方向的滑动增加,就会产生蠕变。橡皮筋向与罐的滚动方向相反的方向蠕动。
2. 相同旋转蠕变
2.1 有限元模拟轴承蠕变机理的研究
为了更好的理解相同旋转蠕变的机理,首先我们以NSK基于有限元分析的结果来进行说明。轴承模型如下所示(无旋转载荷)
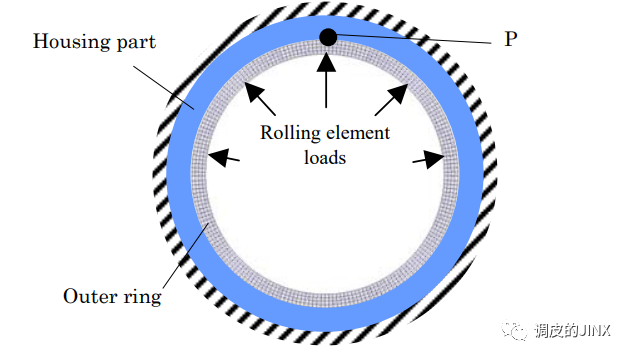
下图显示了轴承外圈的弹性应变分布的结果。图(a)为周向应变的分布,图(b)为径向应变的分布,图3(c)中的曲线图显示了外圈外径上的应变分布。

在基准点P附近的外径的局部区域内,周向应变εθ为正值,径向应变εr为负值。 这表明在轴承外圈与壳体之间的接触压力下,外圈在圆周方向上拉伸并且在径向上收缩 。显然,当轴承载荷沿内圈旋转方向旋转时,局部应变的分布相应地沿相同方向移动。
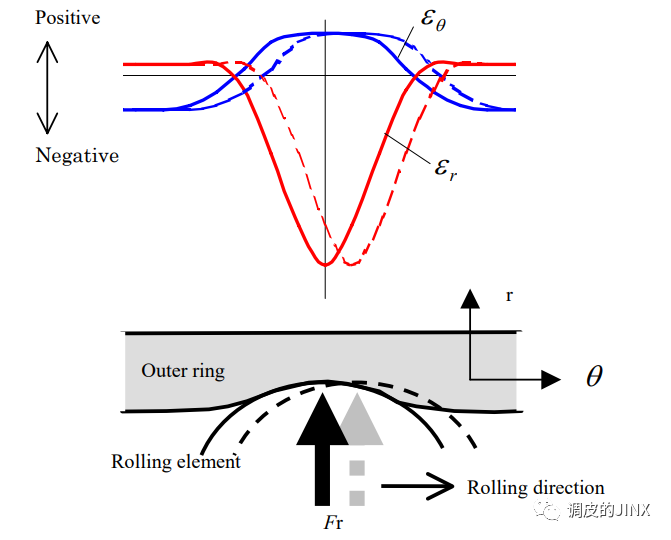
下图给出了与轴承运动相关的应变变化(Δεθ,Δεr)的分布。根据轴承的运动方向,应变变化在前后有不同的分布。Δεθ的分布在轴承的前面正值,在其后面负值。同时,Δεr在滚动元件前面负值,后面正值。
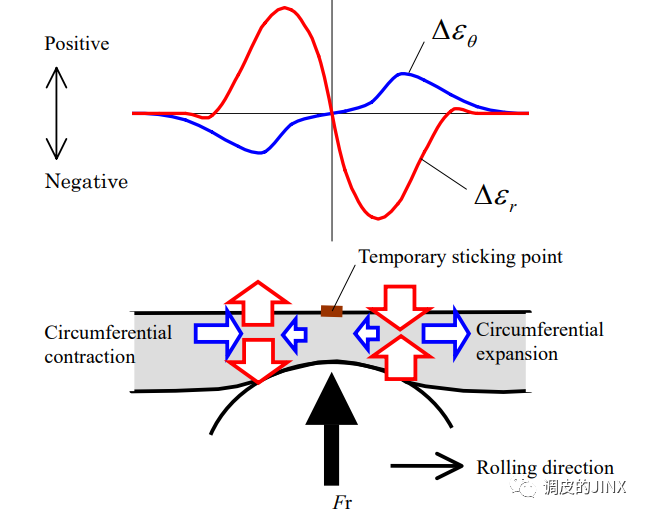
也就是说,在圆周方向上,轴承滚珠的每次通过都会反复发生前面的局部拉伸和后面的局部收缩 。
为了验证上述有限元分析的准确性,研究者进行了实测试验。在该测试中,通过摄像机记录了外圈蠕变,便于计算蠕变速度。在测试中,使用通过连杆连接到外圈的称重传感器测量蠕变扭矩。同时,在驱动轴上测量了轴承的动态扭矩。

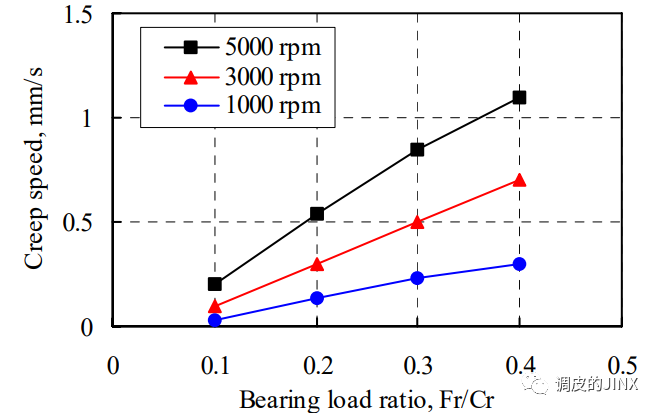
试验结果如下所示:
- 外圈蠕变速度随着内圈的旋转速度而变化,并随着轴承负荷的增加而增加
- 蠕变转矩和动转矩随着轴承负荷的增加而增加
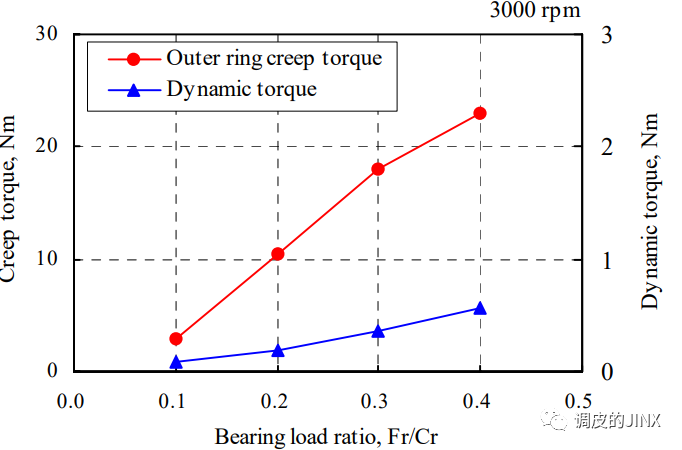
- 蠕变转矩和动转矩随着内圈转速的增加而几乎没有变化

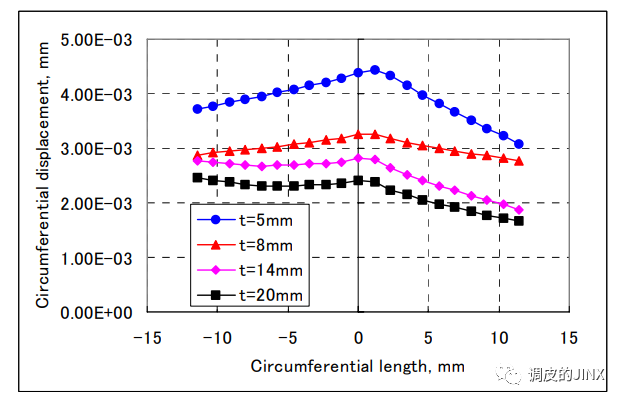
除了轴承的载荷和内圈的转速外,还有许多因素,如外圈的刚度,滚动元件的数量,轴承座与外圈之间的间隙等,都会影响外圈蠕变的可能性。下图显示了出了针对不同厚度的壳体(t)的周向位移的变化。 明显的趋势是,外圈蠕变可能在具有较小刚度的较薄外壳中容易发生。 通过有限元模拟和测试,得出结论,非旋转载荷下的外圈蠕变是滚动体引起的局部应变和波纹变形的结果。
2.2 基于行波原理的轴承蠕变研究
在另外一项研究中,研究者提供了一个假设: 轴承外圈表面上产生了行波 (行波是指平面波在传输线上的一种传输状态,其幅度沿传播方向按指数规律变化,相位沿传输线按线性规律变化) ,该行波移动了轴承外圈并产生了蠕变 。使用有限元分析,可以相对容易的理解蠕变,但无法指出蠕变是行波传播的现象。因此,研究者使用熟悉的设备来解释这种机制,并讨论产生行波原理来限制蠕变的条件。
在盘型超声波马达中,行波被弹性体表面上的压电元件激发。这在转子上沿与弹性体的表面上的行波相反的方向产生椭圆运动。
下图示出了超声波马达的传递机构。压在弹性体上的转子通过表面的椭圆运动沿与行波相反的方向移动。
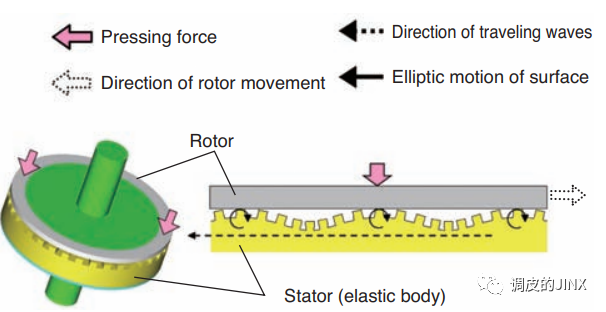
随着轴承外圈的蠕变,行进波会产生到外圈本身。就蠕变方向而言,外圈在滚动体行进方向的相反方向上作用在壳体上。然而,由于壳体是固定的,所以将外圈推回,导致其沿与滚动元件相同的方向行进,即沿与轴承旋转方向相同的方向旋转。

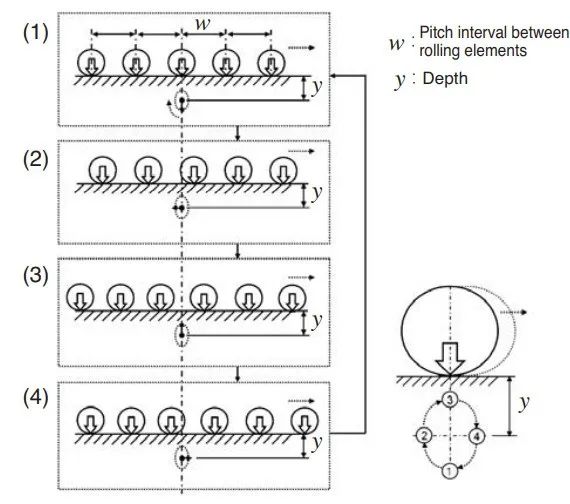
来自行进的滚动元件的载荷施加在主体的表面上时,位于主体的相对浅的区域处的点以环形运动。当滚动元件刚好经过(1)上方时,该点被向下压,而当该点位于两个滚动元件(3)之间时,该点向上移动更靠近表面。在这些位置(2)和(4)之间,它移动到滚动元件的相对侧。因此,轴承在旋转过程中会不断重复这种微观行为,也就是所谓的行波。
研究者通过Bussinesq位移方程建立轴承微观内部微观位移计算模型,在该模型中,假设qi遵循正弦函数分布。


下图显示了上述模型的利萨如图形( 由在互相垂直的方向上的两个频率成简单整数比的简谐振动所合成的规则的、稳定的闭合曲线)。通过利萨如图形,可以清晰的知道不同情况下,振幅A的变化。

通过分析,研究者得出以下结论:
- 外圈局部幅度A与轴承载荷成正比
- 当轴承壁厚/轴承滚珠之间的距离比值达到一定时,轴承载荷对外圈局部幅度A几乎无影响,即已收敛


总结
本文是电机轴承蠕变专题的第一篇,分享了轴承外圈两种蠕变的机理研究。无论是哪一种机理,研究者的研究对象都是轴承本体,因此在分析电机轴承蠕变问题,我们要充分考虑到系统的复杂性(轴承外圈与轴承座有间隙、电机系统存在磁拉力、电机系统存在不平衡等),不能盲目的套用任何一种理论。
当电机轴承发生蠕变,轴承外圈与内圈旋转方向是什么样呢?
一直同向还是一直反向,或同向和反向同时存在(存在某一状态临界点)?
-
轧机减速机轴承跑外圈如何修复的2024-03-14 312
-
电机轴承发热和损毁的原因2023-10-07 3095
-
电机轴承发热损毁的常见原因2023-09-24 2778
-
电机轴承噪声为什么这么麻烦?为什么电机轴承噪声问题这么难呢?2023-07-28 1312
-
电机轴承温度的时域与分布分析2023-07-21 1130
-
驱动电机轴承电腐蚀原罪—趋肤效应2023-07-18 1856
-
减速机轴承跑外圈怎么处理2022-12-08 629
-
轧机轴承外圈爆裂的原因及对策 压缩机轴承温度高的处理方法2021-12-13 2255
-
伺服电机轴承过热的原因是什么2021-06-28 1699
-
影响电机轴承系统问题的因素有哪些2020-08-25 2138
-
电机轴承发热的要素及处理办法2020-05-01 2802
-
电机轴承设计“8不要”保证安全运行2018-10-18 4114
全部0条评论

快来发表一下你的评论吧 !



