PWM调制器在小信号环路中，究竟是何等效模型？

本文将继续研究电压模式Buck，从频域边带效应和多频率模型的角度，深度揭秘：

• PWM调制器在小信号环路中，究竟是何等效模型？在中高频段，小信号的精确模型与传统平均模型的偏差何在？
• 在中高频段，精确的小信号模型与真实PWM变换器的系统是否仍有偏差？

LTI系统频率响应的适用性

频率响应，即稳态下线性时不变(LTI)系统的幅值/相位随频率的变化。它反映了任意频率下，系统正弦输出和对应正弦输入的一一对应关系，且LTI系统的输出响应和输入信号的注入时刻无关。

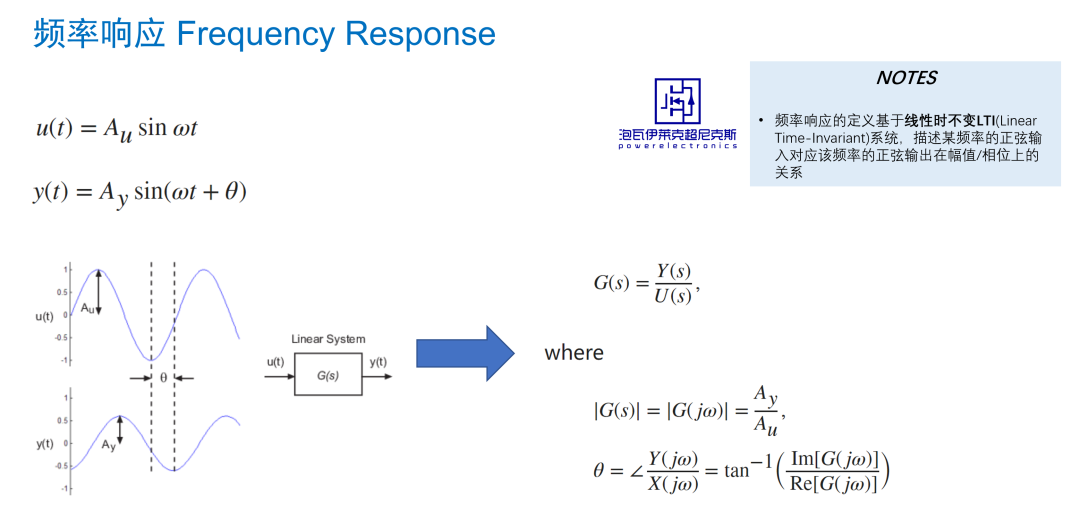
LTI系统频率响应的定义

然而，前文提过PWM调制器具有时变的采样特性，时变系统本身已经破坏了LTI系统的分析基础。若从频域上考察PWM变换器，在闭环回路中注入一个接近fsw的高频扰动 fx ，可以明显看到Buck的输出电压* vo存在一个 ** fsw -fx的差频响应(beat frequency)，这是由于fx经过开关频率fs的载波自然采样下的边带效应造成的。如此，系统在某频率下的输出响应并不仅仅由该频率的扰动输入贡献，这是LTI系统频率响应无法描述*的特性。

非LTI系统中频率响应不再适用

PWM变换器的时变特性，导致越往高频处越远离一个LTI系统，在LTI波特图理论下的频响指标(带宽/稳定裕量等)参考价值越低。有学者提出利用线性周期LTVP/LTP系统理论建模和分析，这是足够严谨的，但分析手段在数学上过于复杂且物理意义并不直观。

小信号精确模型的意义

在介绍系统大小信号建模时，已简单归纳过小信号建模的部分手法，本文将中高频小信号精确建模的途径重新归纳如下。

小信号精确建模的方法分类

PWM调制器在中高频的时变特性已然不可忽略，势必造成使用LTI系统理论下的小信号模型，即便是环路分析仪直接扫频的结果，也无法精准描述实际PWM变换器的全部特性(下图可形象说明这个问题)。但是，从理论上建立小信号精确模型仍然是有必要的，因为 频率响应和波特图分析方法是工程实践普遍接受的设计习惯 ，精确建模可在中高频无限接近实际的环路扫频结果，从而给基于频率响应的 环路补偿和高带宽设计提供理论指导 ，同时也可从小信号频域的角度大致预测中高频的不稳定行为(如次谐波振荡)。另一方面，基于平均模型的建模思路不断改进而来的频域精确建模方法，最容易被工程实践人员理解和使用。

各数学模型的关系

既然通过频域波特图设计环路依然是工程实践的绝对主流，本文将从频域的角度介绍边带效应和多频率小信号精确模型，以帮助大家理解PWM调制器在中高频究竟带来了什么。

边带效应和频率混叠/耦合

下图通过例子说明了开环的PWM调制器，自然采样下的时变特性：占空比的输出响应和输入调制波的注入时刻相关。

PWM调制器自然采样的时变特性

开环情况下，如果把PWM调制器看做fsw的采样环节，调制波在某频率的小信号扰动输入下，会在频域以nfsw为中心，产生周期性的延拓，这些因fsw采样产生的高频信号称为 **nfsw **的 边带效应 。

PWM调制器的边带效应与频率混叠

然而，闭环中的PWM调制器比仅考虑开环PWM调制器的特性更为复杂。环路是一个低通滤波器，调制波的扰动产生的边带会在闭环绕一圈后重新回到调制器参与调制，导致PWM占空比输出的响应既含有扰动频率成分，又含有各边带频率成分， 扰动频率和边带频率相互耦合 (有文献也称这种耦合是PWM调制器的频率混叠，这取决于频率混叠如何明确定义)。

PWM调制器的边带效应在考虑闭环以后的频率耦合

由上图容易知道：扰动频率越高，越接近 nfsw * ，则越容易在低频处产生差频的输出响应； 且环路的带宽设计得越高，更多落在低频的边带成分将被有效放大，边带效应造成的频率耦合越严重 ，传统的小信号平均模型造成的误差是非常显著的。

频率越高，越不可忽略边带效应和闭环的频率耦合

多频率模型

逐步考虑高频和大纹波

基于频域边带的小信号精确建模被称为“多频率模型”，始于CPES邱阳在2005年左右的研究，考虑采样带来的高频边带效应以及在闭环系统中的频率耦合。

多频率模型的发展

近年来，众多学者对邱阳多频率模型的精度不断优化，考虑的边带数越来越多，配合对大幅度调制纹波具体形状的分析，可以突破“低频假设”和“小纹波假设”的双重限制，求得和环路分析仪扰动法扫频几乎一致的结果。

不同多频率模型考虑的边带数

在调制波幅值和载波相比不可忽略的情况下，调制波含“大纹波”对小信号全频段增益和中高频段相位带来的影响也是显著的。学术界从引入纹波的开关频率正弦基波开始，结合多频率模型共同分析。

调制波是“大纹波”情况下对小信号模型的影响

为了同时解决所有高频边带和所有纹波频率分量对小信号的影响，本文引用南航李鑫博士的“拓展频率模型”及其结论说明PWM调制器在小信号模型中的特性。

拓展频率模型

完整的PWM调制器小信号模型

在已知补偿器参数进而考虑“大纹波”形状的PWM调制下，结合边带效应和闭环频率耦合，可得到一个完整的PWM调制器小信号模型。下图给出的是PI补偿器的闭环Buck，其PWM调制器的小信号传递函数GPWM的近似结果。

PI补偿的闭环Buck，完整的PWM调制器小信号模型GPWM

由下图的例子可以明显看到：

• GPWM不再是平均模型中的恒定增益，而是和纹波形状(补偿器参数、主电路参数、开关频率、占空比共同决定)相关
• GPWM近似为一阶系统，在平均模型1/Vm基础上多了一个增益调节量和一个极点，它们均和补偿器的Kp相关(一个正相关，一个反相关)
• 试图提高带宽的过程中，增大补偿器Kp往往会增大全频增益，但会降低中高频的相位，无法保证充足的相位裕量
• 有两点可能性是相当反直觉的，因GPWM的增益调节量和极点均可正可负：
  ①有时，增大补偿器Kp反而有可能降低 GPWM的增益 ，导致环路增益和带宽不再提升
  ** ②有时， 极点也有可能成为右半平面的开环不稳定极点**

GPWM和小信号环路随增益Kp的变化趋势

两个反直觉的实例

尝试把带宽提升到逼近fsw/2

综上所述，我们将PWM调制器的特点总结如下。

用边带效应理解PWM调制器的总结

当我们试图通过增大补偿器Kp，尽可能地提升带宽直至逼近 fsw /2的过程中，不难遇到上述两点反直觉的可能性，即增大补偿器Kp对环路增益/带宽的提升无效，和产生中高频的右半平面极点。如下的仿真实例可以印证。

必须再次强调，正如本文一开始所谈的那样，从结果上看，带宽可以提高直到逼近 fsw /2系统仍是稳定的，但此时依然是基于LTI系统理论的分析手段，波特图上的带宽和相位裕量等指标已经部分失去了参考价值。 这也是设计经验提示我们要把小信号环路的带宽设计在开关频率1/10-1/5范围内的深层原因 。