为什么使用有源组件？讲讲有源滤波器

介绍

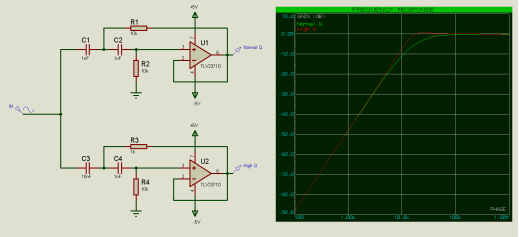
有源滤波器将有源元件引入滤波电路;有源元件是由外部电源而不是信号本身单独供电的组件。通过在滤波器后增加一个缓冲运算放大器，我们可以用信号驱动更高的负载而不会衰减。下面为高通滤波器示例：

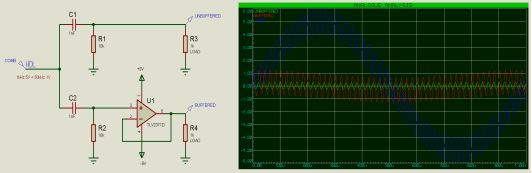
请注意观察，与缓冲输出（红色迹线）相比，无缓冲输出（绿色迹线）的衰减程度如何显著增强。

为什么使用有源组件？

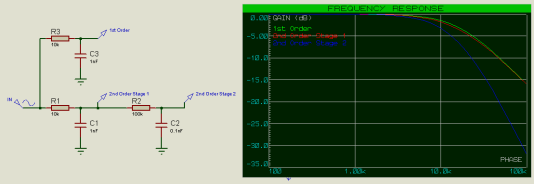
在高阶滤波器链中添加缓冲器还可以减少链中每个环节之间的衰减，并防止链中的滤波器元件扭曲链中其他滤波器元件的滤波器特性。如果我们以下面的二阶低通滤波器为例，那么我们可以看到，第二滤波器看到的电阻元件不仅仅是R2=10k，而是R1 + R2 = 20k，第一个滤波器看到的电容不仅仅是C1的电容，而且C2的电容也需要考虑在内。

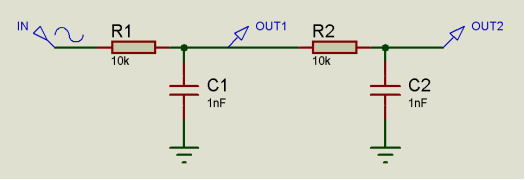
得出：Cutoff Frequency = 1/2πRC（截止频率=1/2πRC）

这具有降低滤波器截止频率的效果。

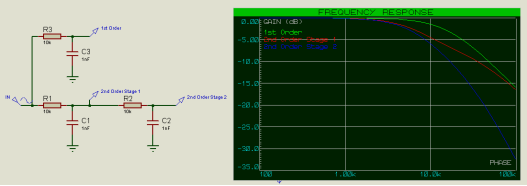
对于 10k 和 1nF 的 R 和 C 值，我们期望截止频率（第一滤波器级为 -3dB，第二滤波器级为 -6dB）为 15.9kHz，但我们看到它略低于此。请注意，二阶第1级的频率响应最初如何遵循二阶第2级的频率响应，因为在低频下，电容器充当开路（好像它们不存在），但是在较高频率下，二阶第1级的频率响应随后跟随一阶滤波器的频率响应，因为C1开始充当短路，与R2相比电阻低。

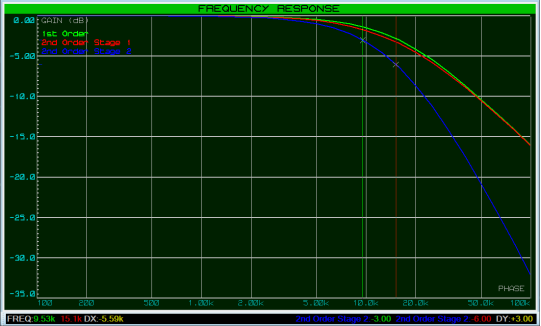
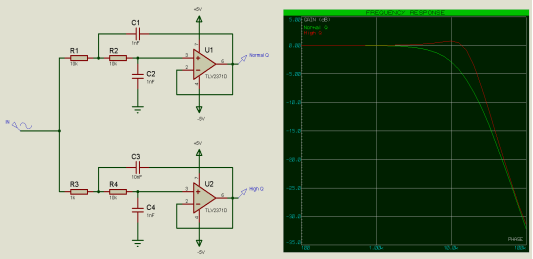
如果我们在滤波器第2级中降低电阻并增加电容（但保持相同的RC常数），则这一点更为明显：

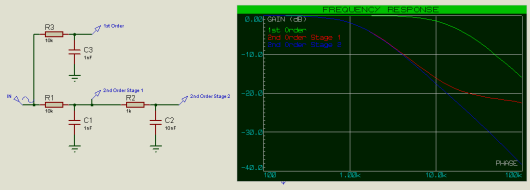
这会将截止频率调低。

缓解这种情况的一种方法是使第2级的输入阻抗至少比第1级的输出阻抗大一个数量级（10倍），即使R2比R1大10倍（C2小10倍，保持RC恒定）。

现在我们可以看到，二阶滤波器第1级的频率响应与一阶滤波器的频率响应非常匹配，截止频率也更接近预期的15.9kHz。

进一步降低第1级的输出阻抗或增加第2级的输出阻抗将继续使截止频率更接近预期;然而，它永远不会完全到达那里，并且添加第 3 个（或第 4 个等）过滤器阶段会使情况进一步复杂化。这就是我们引入有源组件的原因。

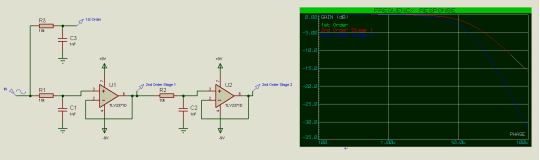
在这种情况下，我们可以看到二阶滤波器的第1级与一阶滤波器的级完全匹配，截止频率如预期的那样为15.9kHz。

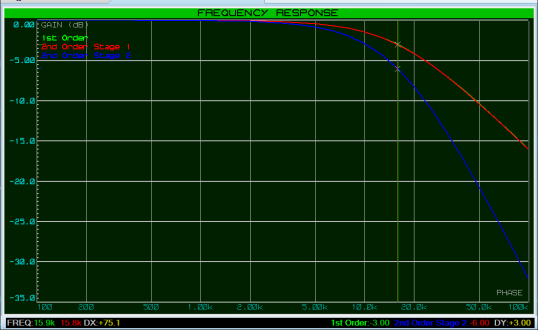我们可以根据需要轻松添加额外的过滤级，以获得所需的滚降清晰度。

请注意，每增加一个滤波器级，截止频率处的衰减（以dB为单位）就会增加-3dB。一阶滤波器在截止频率处的衰减为-3dB，二阶滤波器为-6dB，三阶滤波器为-9dB，依此类推。

Sallen-Key拓扑结构

Sallen-Key 拓扑是一种流行的二阶滤波器拓扑，它使用单个运算放大器。

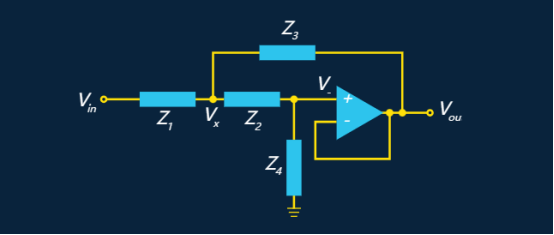Z 元件的选择取决于是否需要低通、高通、带通或带阻滤波器。

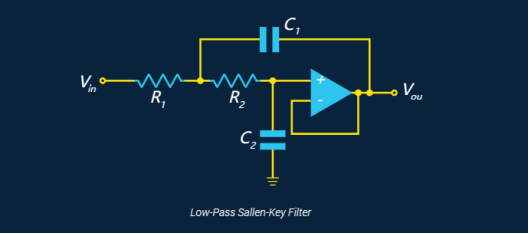
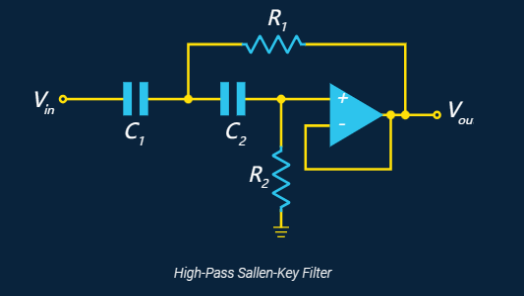
也可以选择添加增益（在运算放大器的反相输入端使用分压器）：

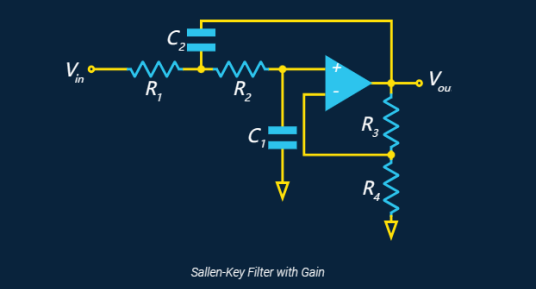
Sallen-Key滤波器的有趣之处在于，第1级不接地，而是连接到运算放大器的输出。这会将来自运算放大器输出的反馈添加回正输入，这可用于增加滤波器的“Q”。

质量系数Q

在科学上，一个振荡系统的质量系数或Q描述了它的阻尼程度（或技术上说，它的阻尼不足--与阻尼相反）。在空气中摆动的钟摆比在水中摆动的钟摆有更高的Q因子；在空气中摆动的钟摆在每次摆动时损失的能量会更少，因此摆动的时间会更长。

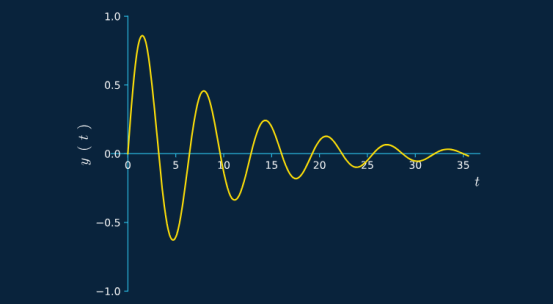
Q = 1表示没有阻尼/欠阻尼，信号幅度保持不变

Q > 1 表示信号被放大（增加）

Q < 1表示信号衰减（减小）

在滤波器响应方面，滤波器的Q值描述了它在截止频率周围的表现（下图为10kHz）：

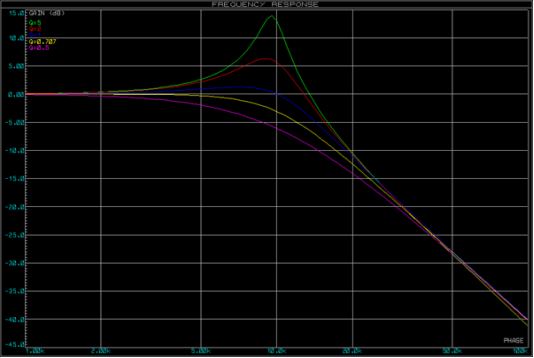
Q > 1将在截止频率下放大信号

Q = 1 将使信号幅度在截止频率下保持不变

Q < 1将在截止频率处衰减信号

另外请注意，Q值越高，截止频率处的拐角越尖。无源一阶滤波器的Q值为0.707（-3dB），无源二阶滤波器的Q值为0.5（-6dB）。然而，使用Sallen-Key有源滤波器拓扑，我们可以为我们的应用选择Q值。例如，我们可能更喜欢Q为1，为我们提供一个滤波器，使信号保持不衰减更接近截止频率，然后在截止频率处具有更清晰的滚降。其工作方式是，来自输出的滤波信号被反馈到输入信号，在截止频率附近与其共振，从而增加其幅度（从而增加Q）。

低通计算

Sallen-Key 滤波器背后的数学原理很复杂，深入分析超出了本文的范围。有在线和离线计算器，可以方便地计算给定截止频率、Q 和增益的 R 和 C 值。然而，我们将简要介绍其中一种简化的情况，其中增益为1（单位），电阻和电容设置为彼此的比率（这类似于我们迄今为止创建高阶滤波器的方式）。

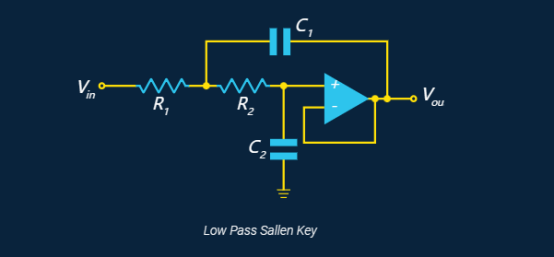
Let R2 = xR1, and C2=(1/x)C1.

这类似于我们之前所做的（当我们创建一个 2 级无源滤波器来减轻对截止频率的影响时），截止频率的公式仍然是 1 / 2πRC。

那么Q=x / (x + 1).

由此我们可以看到，如果 x=1（两个阶段的分量值相同），那么我们得到的 Q 为 1 / （1 + 1） = 1/2 = 0.5;这与我们使用通常的 2 级滤波器 （-6dB） 获得的 Q 相同。但是，如果我们将 x 增加到 10，那么我们得到的 Q 为 10/11 = 0.91，这比我们之前的要高得多。

高通计算

这里的计算方法都是一样的，所以还是让R2=xR1，C2=(1/x)C1。

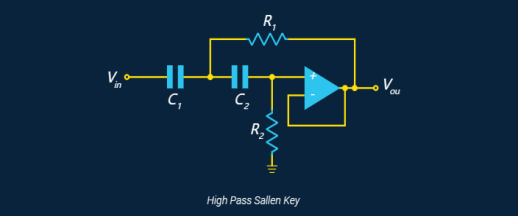
对于 x = 1，我们再次得到 Q = 0.5，对于 x = 10，我们再次得到 Q = 0.91。

*本文章版权归英国LABCENTER公司所有，由广州风标电子提供翻译，原文链接如下：*https://www.labcenter.com/blog/sim-active-filters/