

Python代码下的PSO实现及Matlab下的粒子群函数分享
电子说
1.4w人已加入
描述
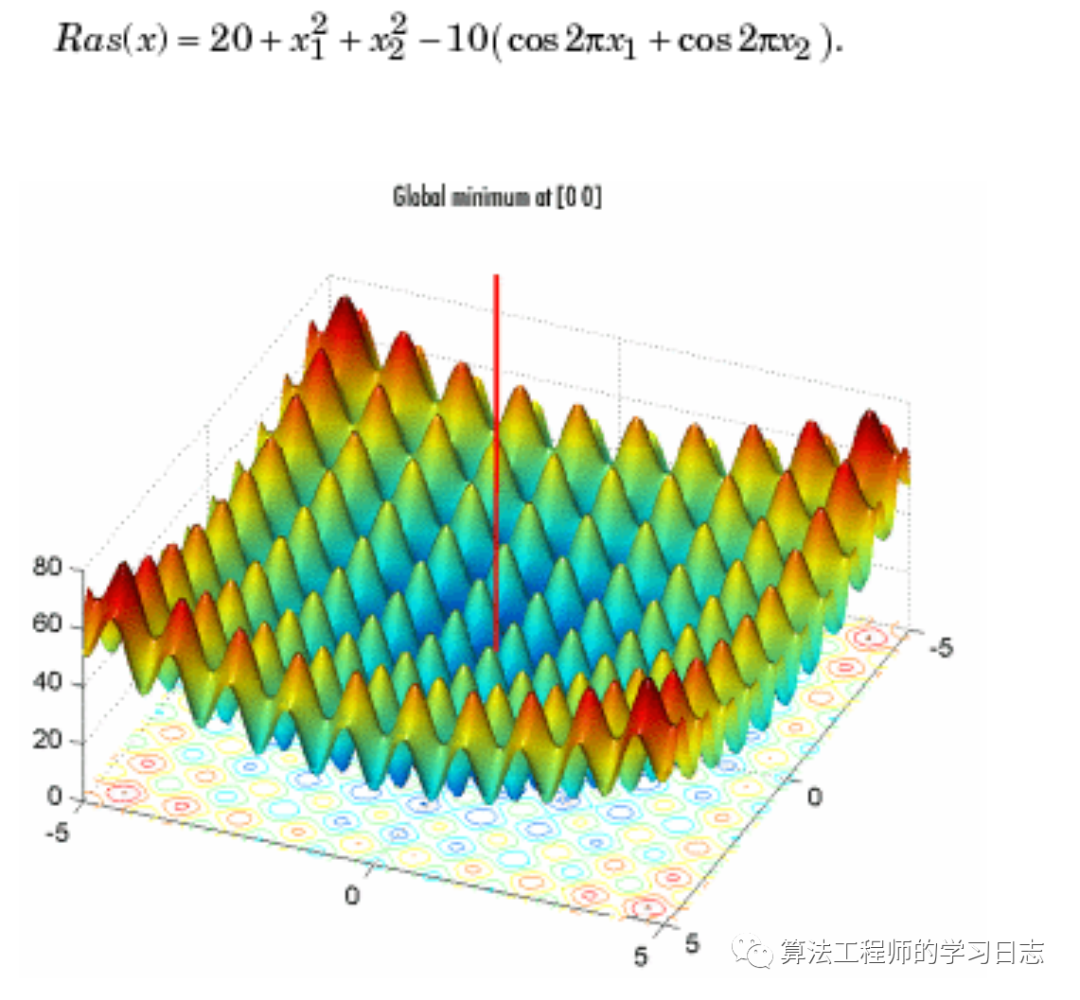
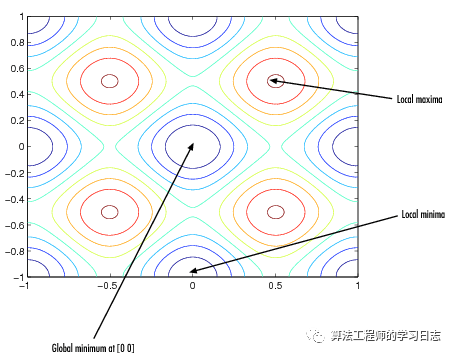
以Ras函数(Rastrigin's Function)为目标函数,求其在x1,x2∈[-5,5]上的最小值。这个函数对模拟退火、进化计算等算法具有很强的欺骗性,因为它有非常多的局部最小值点和局部最大值点,很容易使算法陷入局部最优,而不能得到全局最优解。如下图所示,该函数只在(0,0)处存在全局最小值0。
Python代码实现
import numpy as np
import matplotlib.pyplot as plt
# 目标函数定义
def ras(x):
y = 20 + x[0] ** 2 + x[1] ** 2 - 10 * (np.cos(2 * np.pi * x[0]) + np.cos(2 * np.pi * x[1]))
return y
# 参数初始化
w = 1.0
c1 = 1.49445
c2 = 1.49445
maxgen = 200 # 进化次数
sizepop = 20 # 种群规模
# 粒子速度和位置的范围
Vmax = 1
Vmin = -1
popmax = 5
popmin = -5
# 产生初始粒子和速度
pop = 5 * np.random.uniform(-1, 1, (2, sizepop))
v = np.random.uniform(-1, 1, (2, sizepop))
fitness = ras(pop) # 计算适应度
i = np.argmin(fitness) # 找最好的个体
gbest = pop # 记录个体最优位置
zbest = pop[:, i] # 记录群体最优位置
fitnessgbest = fitness # 个体最佳适应度值
fitnesszbest = fitness[i] # 全局最佳适应度值
# 迭代寻优
t = 0
record = np.zeros(maxgen)
while t < maxgen:
# 速度更新
v = w * v + c1 * np.random.random() * (gbest - pop) + c2 * np.random.random() * (zbest.reshape(2, 1) - pop)
v[v > Vmax] = Vmax # 限制速度
v[v < Vmin] = Vmin
# 位置更新
pop = pop + 0.5 * v
pop[pop > popmax] = popmax # 限制位置
pop[pop < popmin] = popmin
'''
# 自适应变异
p = np.random.random() # 随机生成一个0~1内的数
if p > 0.8: # 如果这个数落在变异概率区间内,则进行变异处理
k = np.random.randint(0,2) # 在[0,2)之间随机选一个整数
pop[:,k] = np.random.random() # 在选定的位置进行变异
'''
# 计算适应度值
fitness = ras(pop)
# 个体最优位置更新
index = fitness < fitnessgbest
fitnessgbest[index] = fitness[index]
gbest[:, index] = pop[:, index]
# 群体最优更新
j = np.argmin(fitness)
if fitness[j] < fitnesszbest:
zbest = pop[:, j]
fitnesszbest = fitness[j]
record[t] = fitnesszbest # 记录群体最优位置的变化
t = t + 1
# 结果分析
print(zbest)
plt.plot(record, 'b-')
plt.xlabel('generation')
plt.ylabel('fitness')
plt.title('fitness curve')
plt.show()
结果为
[0.99699579 0.00148844]
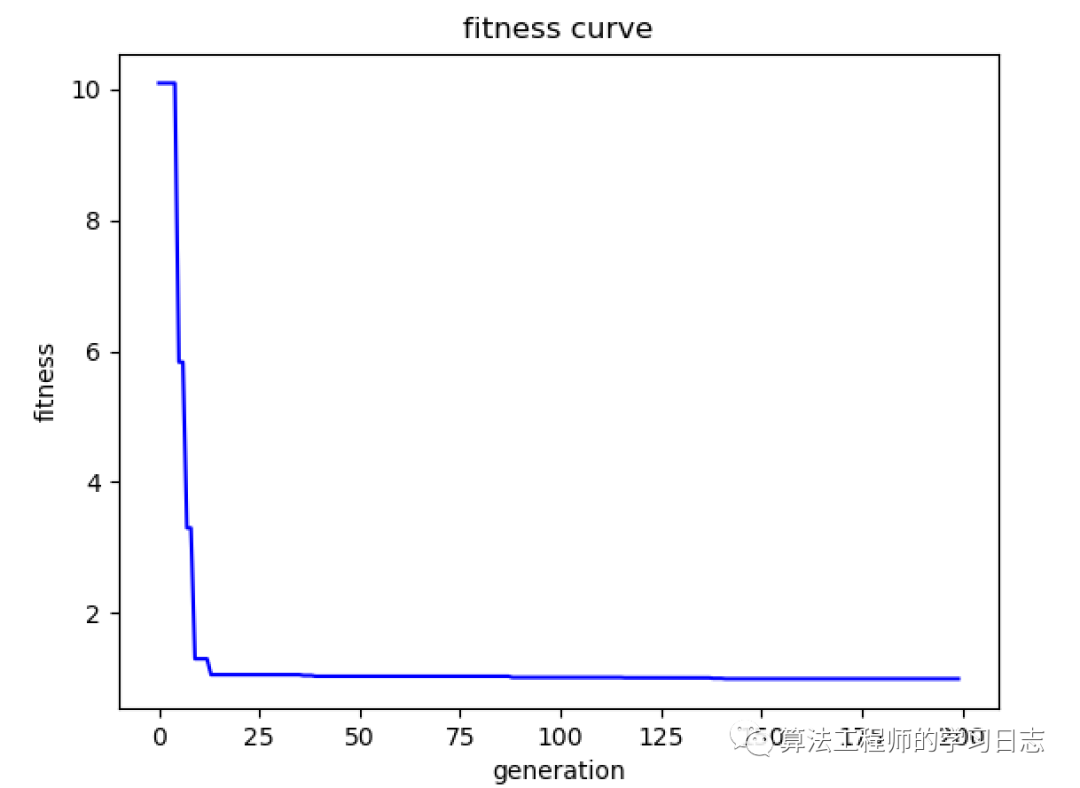
可以知道求解的点非最小值,算法陷入了局部最小值。
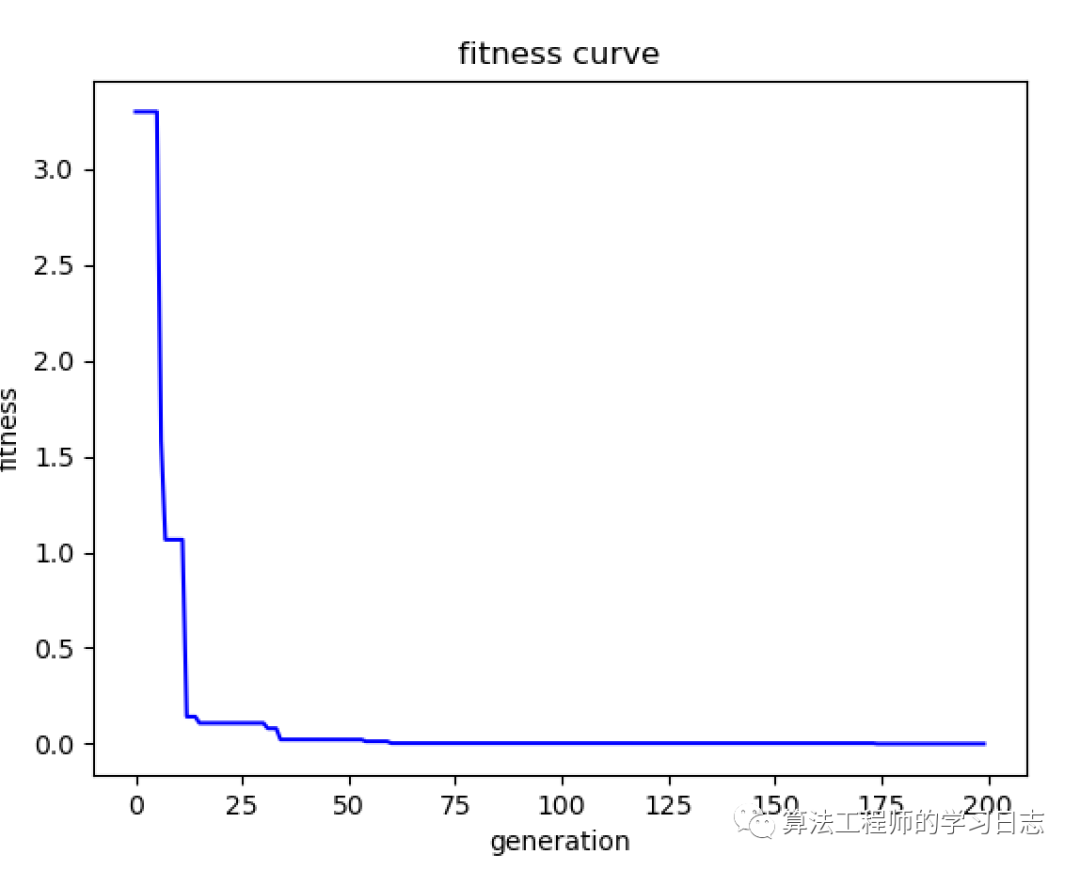
删除自适应变异部分的注释,运行后结果如下,可以看出收敛到全局最优解。
[0.00022989 0.00014612]
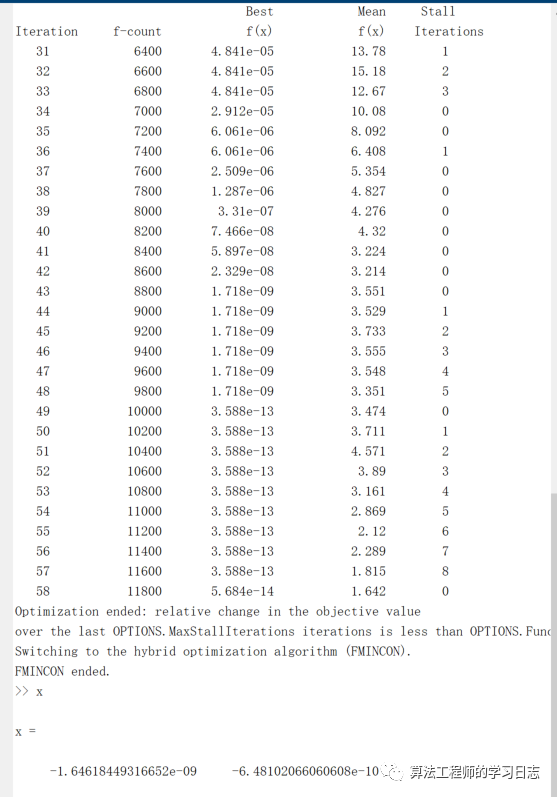
Matlab有个自带的粒子群优化函数particleswarm也可以使用。本例的代码如下:
y = @(x) 20 + x(1).^2 + x(2).^2 - 10*(cos(2*pi*x(1))+cos(2*pi*x(2)));
rng default
options = optimoptions('particleswarm','SwarmSize',200,'HybridFcn',@fmincon,'MaxIterations',200, 'Display','iter');
lb = [-5 -5]; % 这是变量的下限
ub = [5 5]; % 这是变量的上限
[x,fval,exitflag,output] = particleswarm(y,length(lb),lb,ub,options);
结果如下
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
粒子群算法的MATLAB实现(1)2023-07-21 3666
-
【物理应用】基于matlab粒子群配电网重构【含Matlab源码 764期】2022-01-12 625
-
基于matlab粒子群配电网重构简介2022-01-03 1839
-
基于模拟退火结合粒子群算法介绍2021-12-29 1437
-
【Simulink】粒子群算法(PSO)整定PID参数(附代码和讲解)精选资料分享2021-09-08 3209
-
粒子群算法城镇能源优化调度问题2021-07-07 1295
-
LabVIEW粒子群优化(PSO)算法实现2019-07-07 5672
-
基于粒子群优化PSO算法的部署策略2017-12-26 1136
-
基于灰度平均梯度与粒子群优化PSO算法的散焦图像模糊参数估计2017-12-21 1513
-
基于似然分布调整的粒子群优化粒子滤波新方法2017-12-04 957
-
基于混合粒子群算法的PID参数寻优2009-05-25 449
全部0条评论

快来发表一下你的评论吧 !

