

计量标准的重复性考核要求
描述
计量标准的重复性是计量标准的主要计量特性之一。
计量仪器的检定结果具有标准性、统一性和一致性和可靠性及可重复性
JJF1033-2008《计量标准考核规范》规定,计量标准的重复性是建标单位必须提供的主要技术指标之一。它是指在相同测量条件下,重复测量同一个被测量,计量标准提供相近示值的能力。
重复性之所以是计量标准的一个主要计量特性,是因为对于大多数的测量来说,测量结果的重复性往往都是测量结果的一个重要的不确定度来源。
计量标准的重复性规定用测量结果的分散性来定量地表示,即用单次测量结果yi的实验标准差s(yi)来表示。当测量结果由单次测量得到时,它直接就是由重复性引入的不确定度分量。当测量结果由N次重复测量的平均值得到时,则由重复性引入的不确定度分量为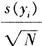 。
。
重复性的测量方法
在重复性条件下,用计量标准对常规的被检定或被校准对象进行n次的独立重复测量,若得到的各次测量结果为yi(i=1,2,……,n),则其重复性s(yi)可用贝塞尔公式计算。
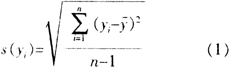
式中:y——n次测量结果的算术平均值;n——重复测量次数,n应尽可能大,一般应不少于10次。
对于可以测量多种参数的计量标准,应分别对每种参数进行重复性试验。
重复测量的次数
由于用贝塞尔公式计算得到的实验标准差s不是标准偏差σ的无偏估计量,也就是说,当用实验标准差s作为标准偏差σ的估计值时,除了存在随机误差之外还会存在系统误差,并且该系统误差随测量次数减少而增大。因此,在使用贝塞尔公式计算实验标准差时,一般要求测量次数较多,在计量标准考核中要求测量次数n≥10。但当重复性引入的不确定度分量不是主要分量时,允许适当减少测量次数,但不得少于6次。
关于重复性条件
JJF1001-1998《通用计量术语及定义》在术语“测量结果的重复性”的定义中指出,重复性条件包括:相同的测量程序,相同的观测者,在相同的条件下使用相同的仪器,在相同地点以及在短时间内重复测量等。
在进行重复性测量时,相同的测量程序,相同的观测者,使用相同的仪器,以及相同地点等要求一般均能得到满足而不会有任何问题。关键是如何理解“在相同的条件下”以及“在短时间内重复测量”这两条要求。
严格地说,要在完全相同的条件下进行两次重复测量是不可能的。这里的“在相同的条件下”应理解为测量时的环境条件应处于统计控制状态下。而要求“在短时间内重复测量”也是为了确保测量时的环境条件基本保持不变。如果测量时间较长,难免环境条件发生变化,因此在进行重复性测量时,测量时间应尽可能短。
在进行重复性测量时,从原则上讲所有的测量条件均应该保持不变。此时在进行重复性测量时应该使该不确定度来源所对应的影响量在合理范围内改变。所谓“合理范围”是指在日常检定或校准中该影响量的可能变化范围。不遗漏,也不重复计算每一个不确定度分量,特别是重要的不确定度分量,是不确定度评定的一项基本原则。
测量对象的选择
由于测量对象本身的不稳定性,并且还可能受到环境条件的影响,因此被测对象也会对测量结果的分散性有影响,特别是当被测对象是非实物量具的测量仪器时。于是由式(1)计算得到的分散性通常比计量标准本身所引入的分散性稍大。
《规范》规定计量标准的重复性应该包括被测对象对测量结果分散性的影响。但由于不同的测量对象对重复性的影响可能不同,因此就产生了应该选择什么样的测量对象来进行重复性测量的问题。
为了使评定得到的不确定度可以用在大多数的同类测量中,《规范》规定重复性试验所采用的测量对象应是常规的测量对象。所谓“常规”的测量对象应理解为其本身的稳定性是绝大多数的被测对象都能达到的,而不能采用稳定性最好的测量对象。无论被检定或被校准的测量对象是否稳定,计量标准的重复性是建标单位必须提供的主要技术指标之一。
被测仪器的分辨力对重复性测量的影响
测量仪器的分辨力是指测量仪器能有效辨别的最小示值差。对于数字式测量仪器,分辨力为变化一个末位有效数字时其示值的变化。对于模拟式仪表,读数时能分辨到几分之一格就是其分辨力。由于测量仪器的分辨力不可能做得无限小,于是测量仪器的有限分辨力也会对测量结果产生影响,若测量仪器的分辨力为δx,则分辨力所引入的不确定度分量为0.289δx。
由于重复性测量中的每一个测量结果都会受到被测仪器分辨力的影响,并且在大多数情况下对不同的测量结果其影响是不同的。因此,在通常情况下,由式(1)计算得到的实验标准差s(yi)同时包含了被测仪器分辨力对测量结果的影响。故此时应只考虑重复性所引入的不确定度分量,而不必再考虑分辨力所引入的不确定度分量。
但如果测量仪器的分辨力太大,而导致由贝塞尔公式计算得到的重复性引入的不确定度分量小于被测仪器的分辨力所引入的不确定度分量,或甚至由式(1)计算得到的重复性引入的不确定度分量等于零时,则应该用分辨力引入的不确定度分量代替重复性分量。总之,由贝塞尔公式计算得到的重复性分量和由被测仪器的分辨力引入的不确定度分量中,仅取两者中的较大者即可。
合并样本标准差
对于常规的计量检定或校准,当无法满足n≥10时,为使得到的实验标准差更可靠,如果有若干组类似的重复性测量数据可以利用,可以采用合并样本标准差sp。其计算公式为
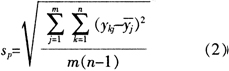
式中:m——测量的组数;n——每组包含的测量次数;ykj——第j组中第k次的测量结果;——第j组测量结果的平均值。
由式(2)计算得到的合并样本标准差的准确程度决定于根式中分母的大小。也就是说,如果每组的重复测量次数n不太大,通过增加所采用的组数m,同样可以得到较为准确的sp。
不是在任何重复性测量中都可以采用合并样本标准差,只有当已经存在若干组类似的重复测量数据可以利用时,才有可能采用合并样本标准差。所谓若干组类似的重复性测量数据是指在不同的时刻对同一测量对象,在规程或技术规范规定的条件下测得的各组重复性测量数据;或者虽然是对不同的测量对象(包括同一测量对象的不同测量点)得到的重复性测量数据,但实验结果或理论分析表明其重复性相差不大。
对重复性的要求
重复性所引入的不确定度,只是测量结果的不确定度中的一个分量。因此,从原则上来说,对重复性本身并无严格要求,只要最终得到的测量结果的扩展不确定度满足要求即可。但由于在新建计量标准时已经对计量标准的重复性进行了测量,并且已经证明最终得到的测量结果的不确定度满足要求,因此,可以将新建计量标准时测得的重复性数据作为判断的初步依据。
如果测得的重复性小于或等于新建计量标准时测得的重复性,则表明计量标准的重复性已满足要求。
如果测得的重复性大于新建计量标准时测得的重复性,在测得的重复性与以往重复性数据相比不存在较大突变的条件下,则应按新的重复性测量数据重新将各不确定度分量合成并得到测量结果的扩展不确定度。当评定得到的测量不确定度仍符合要求,判重复性符合要求,否则判为不符合要求。在任何情况下重复性的较大突变都是应该寻找原因并将其消除的。
《规范》规定,除了新建计量标准时应当进行重复性试验,并提供测得的重复性数据外,已建计量标准应至少每年进行一次重复性试验,并判断其是否符合要求。
对于已经有效建立测量过程统计控制的计量标准,由于控制图本身已经提供了大量的重复性测量数据,因此可以不必再单独进行重复性试验。
在计量标准考核中,我们关心的不仅是测量结果的不确定度到底是多少,更重要的是在最坏的情况下其测量不确定度是否仍能满足要求。
-
MFC测量重复性不高怎么回事?2024-10-23 1299
-
立仪科技光谱共焦应用之金属隔膜静态重复性测量2024-08-09 658
-
深视智能光谱共焦位移传感器检测透明玻璃平面度重复性2024-08-05 890
-
PySnooper:替代print的重复性工作2023-10-30 853
-
计量标准的重复性考核要求2022-03-18 4567
-
流量计重复性差的解决方法2022-01-05 1952
-
PGA-SAR系统无法达到12比特级别的可重复性时,Δ-Σ系统会怎么样呢?2021-04-07 1058
-
计量标准重复性的测量方法2020-11-12 22700
-
机器人技术的可重复性和准确性分析2020-09-17 3397
-
计量标准的重复性是计量标准的主要计量特性之一2018-08-08 8245
-
并行传感器如何提高倾斜测量的精度和可重复性2018-07-11 3758
-
基于赛灵思FPGA设计的整体时序具有完全可重复性2017-11-24 1005
-
相控阵探头的重复性与可靠性2010-03-20 595
-
测量系统的的重复性和重现性2009-08-16 1470
全部0条评论

快来发表一下你的评论吧 !

