MATLAB在数学中的应用有哪些？

• 多项式及函数

1.多项式的表示

MATLAB用一维向量来表示多项式，如多项式

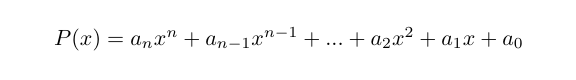
表示为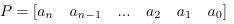,缺少的幂次系数用‘0’补充

2.多项式求根

求多项式的根即求使多项式为0的值，也即数学中的零点问题，MATLAB提供了 roots函数求根 ，用法如下：

 > > P=[1 2 1];%x^2+2x+1=0
 > > roots(P)
ans =
    -1
    -1

根据多项式的根反求多项式则用 poly函数 ,一般多项式是行向量，根是列向量，例如：

 > > r=[-1;-1];
 > > poly(r)
ans =
     1     2     1

3.多项式四则运算

加法：如果两个多项式大小相同时，则多项式相加与标准的数组加法相同

乘法：使用conv函数

除法：使用 deconv函数 ，[a,r]=deconv(b,c)其中a为b除c的商，r为余数

 > > a=[1 1];b=[1 -1];%(x+1)*(x-1)
 > > c=conv(a,b)
c =
     1     0    -1
 > > a=[1 3 1];b=[1 1];%x^2+3x+1除x+1
 > > [c,d]=deconv(a,b)
c =
     1     2
d =
     0     0    -1

4.多项式的导数、积分及其计算

导数：函数polyder可以实现多项式的求导

积分：函数 polyint(P,k) 返回多项式P的积分,积分常数项为k，默认值为0

计算：函数 polyval(P,x) 返回多项式在x处的值，x可为标量也可为向量

 > > a=[1 2 1];polyder(a)
ans =
     2     2
 > > a=[1 2 1];b=polyder(a)
b =
     2     2
 > > polyint(b,3)
ans =
     1     2     3
 > > polyval(a,1)
ans =
     4

5.有理多项式

函数 [r,p,k]=residue(num,den) 可执行部分分式展开的的运算，等式两边互换可实现逆运算

 > > num=[2 -19 29 40];
 > > den=[1 -15 68 -96];
 > > [r p k]=residue(num,den)
r =
    4.0000
    5.0000
    2.0000
p =
    8.0000
    4.0000
    3.0000
k =
     2

本例结果可表示为：

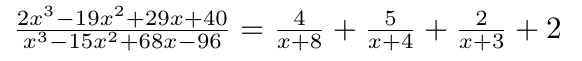
• 数据插值

数据插值是指数据缺失时所进行的一种处理，在数据分析、图像处理等很多领域经常用到，参加过数学建模比赛的小伙伴可能也用过，有多项式插值、分段插值、三角函数插值等。

1. 一维函数插值

当插值函数y=f(x)一元函数时为一维插值，使用interp1函数，语法格式为 **Vq=interp1(X,V,Xq,str)** :X为自变量取值范围，V为函数值或一向量，长度与X一致，Xq为插值点向量，str为字符串变量，设定插值方法。

str='nearest'： 邻近点插值 。插值点的值为与该插值点最近的数据点函数值。速度快但平滑性差。

str='linear'： 线性插值法 。根据相邻数据点的线性函数估计插值点的值。占用的 内存比邻近点多，运算时间长 ，但其结果是连续的，顶点处斜率会改变。

str='spline'： 三次样条插值 。在相邻数据点建立三次多项式函数确定插值。运算时间最长，但平滑性最好。此外还有'pchip'，'cubic'，'v5cubic'等。

y=interpft(x,n) 为一维快速傅里叶插值。当数据点呈现周期分布时，用傅里叶变换把输入数据x变换到频域，然后用更多点n的傅里叶逆变换变回时域，其结果是对数据进行增采样。

x=0:10;
y=sin(x);
z=interpft(y,20);
xx=linspace(0,10,20);%生成0到10之间20个线性等分点
plot(x,y,'-o',xx,z,':o')
legend('原始数据','插值结果','Location','North')

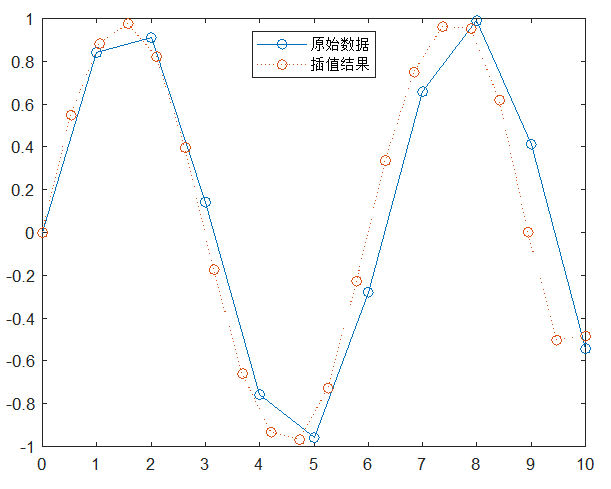
2.二维数据插值

当插值函数y=f(x)为二元函数时为二维插值，语法格式为 **Vq=interp2(X,Y,V,Xq,Yq,str)** 其中X,Y,V是具有相同大小的矩阵，V(i,j)是数据点[X(i,j),Y(i,j)]上的函数值；Xq,Yq为待插值数据网格，str为字符串变量表示不同的插值方法，和一维的相似，例如

[X,Y]=meshgrid(-10:0.25:10);%产生数据栅格点
Z=peaks(X,Y);  %计算已知点的函数值
[x,y]=meshgrid(-10:0.05:10); %产生更精密的插值点
z=interp2(X,Y,Z,x,y);
mesh(X,Y,Z),hold on;
mesh(x,y,z+20),hold off;
axis([-3 3 -3.5 3.5 -6 30])

• 函数极限

极限概念很简单，在中学时就有所接触，这里只简单介绍一些使用极限的函数

limit(fun,x,a) ：当x趋于a时，返回函数fun的极限值。

limit(fun)：默认当x趋于0时求极限

limit(fun,x,a,'left') ：求左极限，还有右极限'right'

• 函数积分

MATLAB支持三重及以下的积分运算

1. 一重积分

一元函数的数值积分有三个函数quad, quadl, quadv用法相同

[Q,num]=quad(fun,a,b,tol,str) fun为被积函数句柄，a,b为积分上限和积分下限，tol用于控制误差，增大tol可加快计算速度但精度下降，str非0时输出计算过程中的[num a b-a Q]，num为函数计算的次数。此函数适用于精度低、被积函数平滑性较差的数值积分。num,tol,str为可选参数

quadl适用于精度高被积函数较平滑的数值积分

quadv用于被积函数是一些列函数的积分

2.二重积分

Q= dbquad (fun,xmin,xmax,ymin,ymax,tol,@quad)

Q=dbquad(fun,xmin,xmax,ymin,ymax,tol,myfun)

MATLAB默认采用quad函数计算一维积分；@quad表示用户指定采用quadl函数来计算一维积分；myfun表示用自己编写的一维积分函数

3.三重积分

Q= triplequad (fun,xmin,xmax,ymin,ymax,zmin,zmax,tol,@quad)后面两个参数为可选项