

MACH3脉冲的工作与输出(三)
电子说
描述
前两篇我们知道了,MACH3的加速度参数之间的关系,那如何用数学公式做出分散的与加速度有关的时间间隔点呢???
我们知道一个物体的加速度有下面几个公式
V=V0+AT;
S=V0 T+1/2(A (T^2));
当V0为0时,则:
V=A*T;
S=1/2*(A*(T^2));
这几个公式都是在连续的时间段时的公式,但CNC只能按步来控制,也就是说这控制时间上时间是分散的,隔离的.
步进加速度分散点如下所示:
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
---------加速----------匀速---------减速-------------
从开始速度最小加速到速度最大(加速),后按最大速度运行(匀速),又从速度最大是降速到速度最小时(减速),每次的时隔不一,
这个怎才能算出来的呢??
推论:
常量:
Steps.per 每mm单位的步值
F 速度
A 加速度
加速到最高速时所用到的参数:
Nm 所用的脉冲数量
fmax 最大时速时的频率(HZ)
Tmax 最大时间
加速到最高速时的频率: fmax= (F/60)*(Steps.per)
加速到最高速时所用到的脉个数: Nm=(fmax*Tm)/2
加速到最高速时所用时间: Tmax =(F/60)/A
加速到最高速时所用脉冲个数: Nmax = (fmax*Tmax)/2
由前几个公式推出分散点n所要时间与参数之间的关系:
Tn^2= (2Tmaxn)/fmax;
Tn= sqrt((2Tmaxn)/fmax);
理论有了,现在就按这个思路写出程序:
<<预处理梯型加速时间表>> ******
因为运算中有开根号与双精度运算,每次所调用的时间很大,为了提供更大的空间给插补运算,
所以提前在程序头中算好所需的时间,填入时间表中
但请注意,这里所需的内存很大,不过为了运行时间,这个还是值的.
#define Steps_per 320
#define Steps_mms 1200 //速度 MM/分钟
#define Steps_A 120
u16 Fmax(u16 Steps_mms_s,u16 Steps_per_s)
{
return (Steps_mms_s/60)*Steps_per_s;
}
double Tmax(u16 Steps_mms_s, u16 Steps_A_s)
{
return (double)(Steps_mms_s/60)/Steps_A_s;
}
u16 Nmax(u16 Fmax,double Tmax)
{
return Fmax * Tmax/2;
}
Fm = Fmax(Steps_mms,Steps_per);
Tm = Tmax(Steps_mms,Steps_A);
Nm= Nmax(Fmax(Steps_mms,Steps_per),Tmax(Steps_mms,Steps_A));
for(i=0;i {
Tn=(sqrt((2*Tm*i)/Fm)*1000000)-Tn_z; //因为算出来为秒,但在程序中用秒为时间单位会太大,所以就换成微秒
Tn_z= sqrt((2*Tm*i)/Fm)*1000000;
}
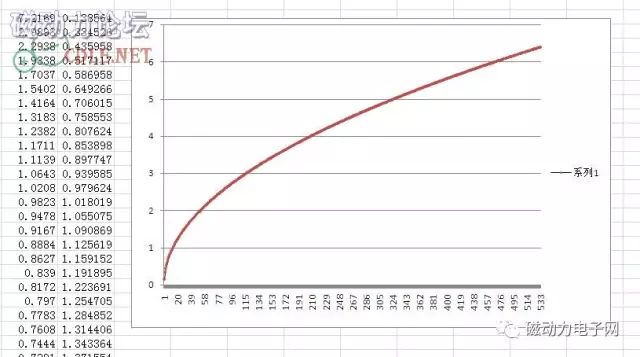
本来是想做到运算器程序里,因本人图个快捷,就电子表格生成一个:
把时间间隔倒数后导入到电子表格中生成如下加速曲线表
这样更直观地反应参数之间的关系
-
mach3控制卡怎样连接伺服2024-06-12 4896
-
MACH3脉冲的工作与输出(一)2023-07-20 4203
-
如何为mach3 bsmce04u连接传感器LJ12A3 4Z/BX2022-11-11 704
-
MACH3软件输入设置2021-09-18 2106
-
深入Mach3内核(中文)2021-08-31 3722
-
mach3雕铣创建2019-05-07 10050
-
Mach3汉化程序软件2014-06-22 1928
全部0条评论

快来发表一下你的评论吧 !

