

MACH3脉冲的工作与输出(四)
电子说
描述
近段来本人的简易CNC控制器有小小突破,也基本上完工了,整理控制器资料时顺手整理了"MACH3脉冲输出",感觉还有两篇没有贴出就接着续篇(基本是按照自问自答的方式出现).....
图片资料可以说是比效珍贵的,请珍惜(最少本人是这么认为的,因为这是MACH3实际输出的波形,并无半点人工干涉,真正想返原它成图并非是一件易事)
上几单元说过了,MACH3控制步进电机是按脉冲方向来完成的,但实际上是怎一回事呢???
最常见的是G0 G1,而G0到底是怎走的呢?? 查阅G指令表: G0是点到点运动的,这在机器是如何运作的呢???
G0 测试
假如从A点到达B点情况是如何呢??
为此本人在通过自己写的软件进行分析MACH3波形实际输出,从而清楚地解决了G0的实际运行方式:
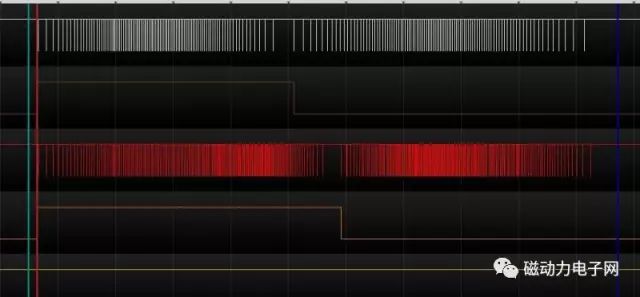
如图所示(G0X1Y1)
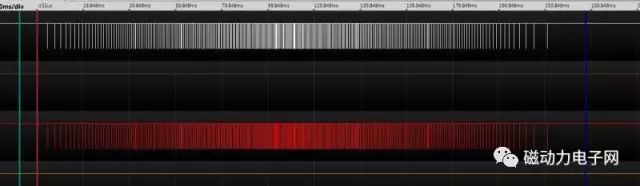
从这个波形来看,可以清楚地知道从A到B有三个过程,一加速过程,二均速过程,三减速过程,这三个过程中对XY来说是完全相同的,清认真看清下图的直线,实际上并非是真正的直线,而是曲线,XY是你一步我一步.你走,我走,你走,我再走,从而在失量合成时就成了一条与X坐标系成45度角的类直线实际效果如图
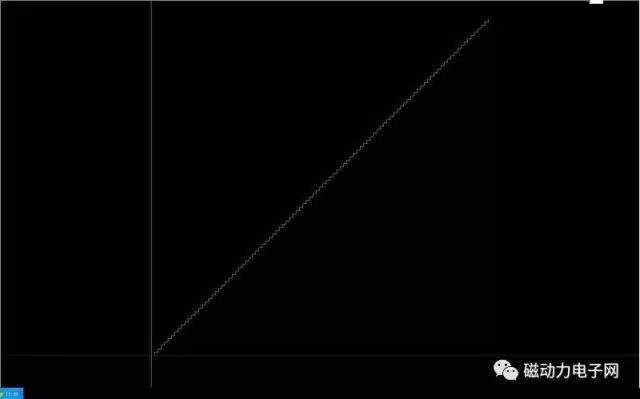
从图中可能清楚地反应:速度从零开始,最后以零结速,加减速度过程并没有改变直线的形状,!!!
这个就是插补的奥妙了!!
有人会说这个简单了,其实本人认为一点也不简单,此过程中所包函的知识太多太多了,各位看官要是想了解更多找渡娘.
G1 测试
接着就是在CNC中起了结定性关键的G1了,
G1到底是什么一个过程呢? 测试两个不同的图形
{
G0x0y0
g1x1y1f1200
g1x1y2
x0y0
}
{
G0x0y0
g1x0y2f1200
x2y2
x0y0
}
直接看图
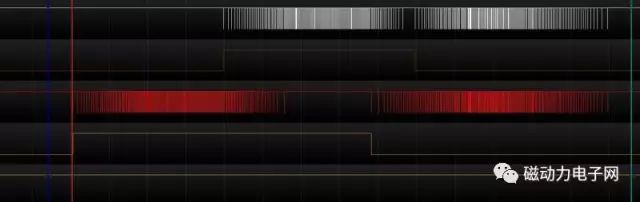

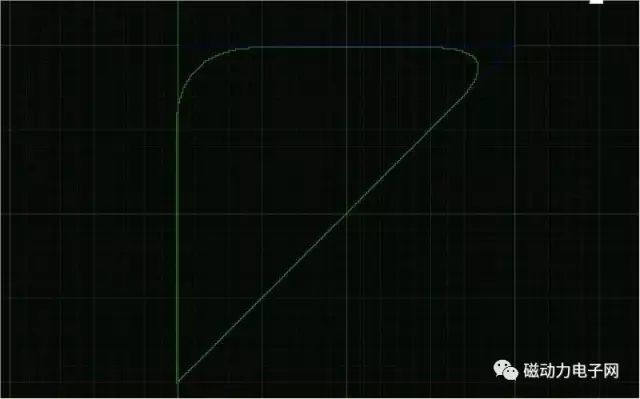
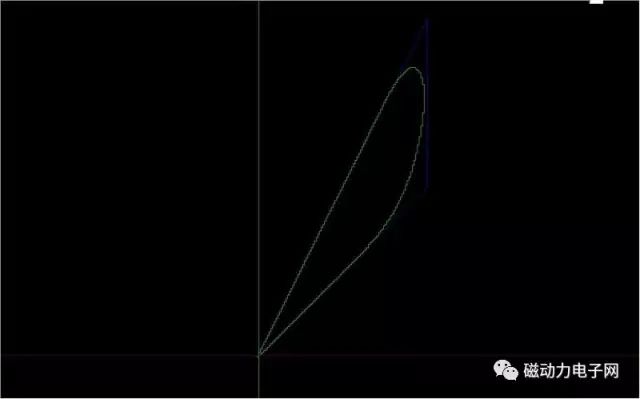
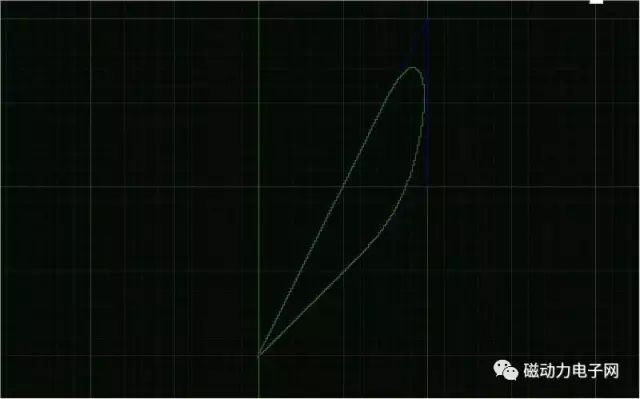
好奇怪的图形啊,为什么会拐弯呢?? 是谁偷了我的锐角呢??
其实一点也不奇怪,因为有牛顿的惯性定侓存在一切物体运动都不能突变,对此MACH3做了一个非常强的拐角过程,以前有网友问过,为什么我的MACH3会出现圆角呢?这个就是给予最好的解答了.
而这个过程是衡量一个CNC好坏的一个关健.为什么会拐得这么漂亮呢?这个拐角方程式又是什么呢? 对于多轴多微线段中,此拐角还可以这么顺吗??此精度又会是多少呢?? 对此本人花了整整二年时间去解读它,也算是有的小成!!
在众多的文献中,很多地方提到插补,而插补的本质是什么? 插补简单来说: 根据给定的数学函数,在理想的轨迹式轮廓上的已知点之间,确定一些中间点的一种方法。直线插补这是车床上常用的一种插补方式,在此方式中,两点间的插补沿着直线的点群来逼近,沿此直线控制刀具的运动。
注意两个字"逼近" 为因为计算机并口输出是脉冲方式,再者步进电机按每步进位一定的距离运行的,所以最后所得到的是一个非标准直线.只能逼近它.
脱离MACH3,假如我们用单片机或自己做的并口输控制,我们有没有方法去实现这个过程呢? 找渡娘后,所知有一种方式比较直接也比较有效那就是"比较法" 如下
直线插补就是零件程序提供直线段的起点、终点坐标,数控装置将这两点之间的空间进行数据密化,用一个个输出脉冲把空间填补起来,从而形成要求的直线轨迹。
(一).偏差计算公式
直线方程 : yi/xi = ye/xe ; 把标准方程变换一下 xeyi - xiye = 0 ,令 实际偏差值是FI 侧实际偏差值 FI = xeyi-xiye
进给方向的选取:使误差减小的方向
当P点在直线上方时;
则:Xeyi - xiYe>0
当P点在直线下方时;
则:Xeyi - xiYe<0
因此:
由F可判别动点P与理想轨迹的相对位置,从而决定下一步移动方向。
F>0,点P在直线上方,应向+X 移动。
F<0,点P在直线下方,应向+Y 移动。
F=0,点P在直线上,为方便,将 F=0 归F>0。
为便于计算机编程计算,将F的计算予以简化。
设第I象限中动点P(xi, yi)的F值为Fi, Fi=Xeyi-xiYe
1.若沿+x向走一步,即
于是有 Fi+1 = Fi -Ye
2.若沿+y向走一步,即
于是有:Fi+1 = Fi +Xe
(二)终点判别的方法有两种:
1.每走一步,判断动点P(xi, yi)的坐标值是否与终点坐标相同,即
Xi-Xe =0且 Yi-Ye=0
若两式同时满足,插补结束。
2.求程序段总步数n=Xe+Ye,每走一步,n-1->n,直到 n=0,插补结束。
知道方法,那程序如何编写呢?? 假如运行至(4,3)坐标:
#include "XXOO.h" //头文件(XXOO笑吧)
void main()
{ int xe,ye,f,j;
xe=4; ye=3; //把常数4写入变量xe;把常数3写入变量ye;
f=0; //把常数0写入f;
j=xe+ye; //读出xe和ye的值,相加后结果写入j;
do {if (f>=0)
{if(ye>=xe) //判断直线是否大于45度;
{cout<<"同时走+x,+y"< f=f+xe-ye; //读出f、xe和ye的值,计算后结果写入f;
j=j-2;} //读出j的值,减2后结果写入j;
else{cout<<"向+x走一步"< f=f-ye; j=j-1;}}
else {if (ye>xe)
{cout<<"向+y走一步"< f=f+xe; j=j-1;}
else {cout<<"同时走+x,+y"< f=f+xe-ye; j=j-2;}}}
while (j!=0);}
是不是很简呢?实际这个是理论上的.而真正的运行是比这个复杂得多得多!!!!!!
此方法中只考虑到象限一,能不能用到四个象限之中呢??
对于第二象限,只要去| x |代替x即可,至于输出驱动,应使x轴步进电机方向旋转,而y轴步进电机仍为正向旋转。
同理,第三、四象限的直线也可以变换到第一象限。插补运算时,取| x |和| y |代替x、y。输出驱动原则是:在第三象限,点在直线上方,向-y方向步进;点在直线下方,想-x方向步进。在第四象限,点在直线上方,想-y方向步进;点在直线下方,想+x方向步进。4个象限各轴插补运动方向如上图所示。由图中看出,F>=0时,都是在x方向步进,不管+x向还是-x向,| x |增大。走+x或-x可由象限标志控制,第一、第四象限走+x,第二、三象限走-x。同样,F<0时,总是走y方向,不论-y向还是+y向,| y |增大。走+y或-y由象限标志控制,第一、二象限走+y,第三、四象限走-y。
假如再加两轴Z+Z-,A+A-,那么问题就大条了.所考虑到的就不是简简单单的比较了,更别说加上速度限定了.
看来"比较法"只能算是初等的算法了,有没有更加高明的手段或算法呢?
-
mach3控制卡怎样连接伺服2024-06-12 4900
-
MACH3脉冲的工作与输出(一)2023-07-20 4210
-
如何为mach3 bsmce04u连接传感器LJ12A3 4Z/BX2022-11-11 704
-
MACH3软件输入设置2021-09-18 2106
-
深入Mach3内核(中文)2021-08-31 3722
-
mach3雕铣创建2019-05-07 10050
-
Mach3汉化程序软件2014-06-22 1928
全部0条评论

快来发表一下你的评论吧 !

