

一种层次权重决策分析方法
电子说
描述
层次分析法(Analytic Hierarchy Process)是美国运筹学家萨蒂于上世纪70年代初,为美国国防部研究“根据各个工业部门对国家福利的贡献大小而进行电力分配”课题时,提出的一种层次权重决策分析方法。其主要思想是根据研究对象的性质将要求达到的目标分解为多个组成因素,并按组成因素间的相互关系层次化,组成一个层次结构模型,然后按层分析,最终获得最高层的重要性权值,其求解过程可以分为以下四步。
1.建立层次结构模型
将所包含的问题分层,可划分为最高层、中间层、最低层。最高层表示需要解决问题的目的,也称目标层。中间层表示实现总目标而采取的各种政策,一般分为策略层、约束层、准则层。最低层用于解决问题的各种措施、方案等,也称措施层、方案层。利用层次分析建立选课的结构层次模型如下:
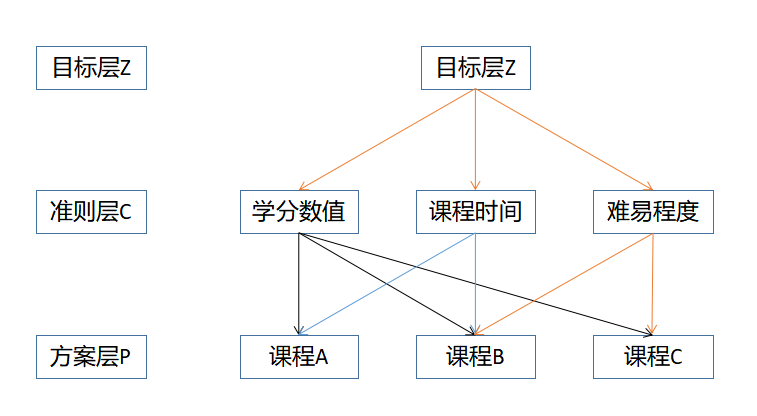
2.构造判断矩阵
由于实际问题的诸多因素通常不易定量的测量,只能根据经验与知识进行判断,一种简单的方法就是两两因素进行比较,从而提高判断的精确性。描述因素相互影响大小的取值也做某种量化,取值为1到9, 的取值可以理解为因素 i 对目标层的影响程度是因素 j 的影响程度的多少倍,或因素 i 对因素 j 的重要程度,矩阵元素的取值及含义如下表:
的取值可以理解为因素 i 对目标层的影响程度是因素 j 的影响程度的多少倍,或因素 i 对因素 j 的重要程度,矩阵元素的取值及含义如下表:

根据上表可得准则层对目标层的判断矩阵A(记为Z-A)

称上述矩阵为正互反矩阵,即aii=1,aij=1/aji。
3.层次单排序及一致性检验
在构造判断矩阵过程中,aij的取值仅注意了ai与aj对目标值的影响,而在确定矩阵各个元素时所采取的标准可能不一致。例如a12=2表示因素a1对目标层的影响是因素a2的2倍,a23=2表示因素a2对目标层的影响是因素a3的2倍,按常推理则a13=4,由于各种实际因素及主观原因确定的a13不等于4,因而需要对矩阵进行一致性检验来尽量减少这种人为主观上的不一致。若正互反矩阵满足:

则称为一致阵,其性质有:
(1)矩阵的秩即rank(A)=1
(2)矩阵的最大特征根为n,其余特征根为0
(3)最大特征根对应的特征向量
由判断矩阵计算被比较元素对于该准则的相对权重,来确定每个因素的排序,称为层次单排序。当考虑的因素较多时,很难保证判断矩阵为一致阵,需要检验矩阵的一致性。令

CI为一致性指数,当CI=0,矩阵为一致阵,CI越大,矩阵不一致程度越大,但对单一的一个矩阵很难说其一致性指数的大小,因而又提出了平均随机一致性指标RI检验判断矩阵是否满足一致性,对于判断矩阵的阶数n,RI取值如下表

令
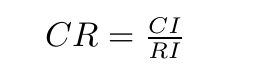
CR为随机一致性比率,当CR<0.1时,判断矩阵有满意的一致性,否则要重新调整判断矩阵使其通过一致性检验(注意各行成正倍数),才可以计算层次单排序的权重。
4.层次总排序及一致性检验
计算同一层次所有因素对于总目标相对重要性的排序权值的过程称为层次总排序,计算和检验都是从最高层向最低层进行的。计算过程为:假设上一层次A一共包含m个因素 ,它的层次总排序权值分别为
,它的层次总排序权值分别为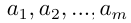 ,下一层次B包含n个因素
,下一层次B包含n个因素 它们对于Aj的层次单排序分别为
它们对于Aj的层次单排序分别为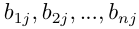 (当
(当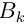 与
与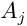 无联系时
无联系时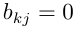 ),此时B层次总排序权值由下表给出:
),此时B层次总排序权值由下表给出:
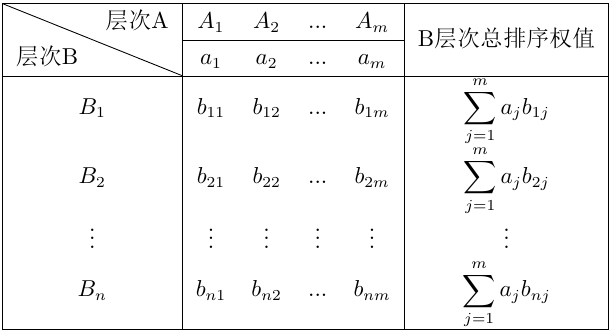
计算中间部分权值时按列看,可以理解为准则层B各因素对目标层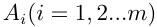 的相对权重;在计算B层次总排序相对权值时按行看,可以理解为
的相对权重;在计算B层次总排序相对权值时按行看,可以理解为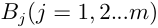 对上一层各因素的权值乘对应因素层次总排序权值的和。层次总排序也要进行一致性检验。设B层中的因素对
对上一层各因素的权值乘对应因素层次总排序权值的和。层次总排序也要进行一致性检验。设B层中的因素对 单排序的一致性检验为
单排序的一致性检验为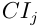 平均随机一致性指标为
平均随机一致性指标为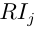 ,则B层次总排序随机一致性比率CR为:
,则B层次总排序随机一致性比率CR为:
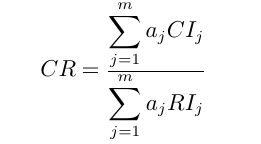
当CR<0.1时,层次总排序结果具有满意的一致性
5.示例
通过前面的层次模型建立判断矩阵后,并通过一致性检验后得准则层各因素对目标层的权值,及其一致性指数CI=0.054
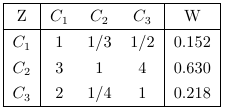
然后构造方案层对准则层的判断矩阵C1-P、C2-P、C3-P,及其一致性指数分别为0.019,0,0
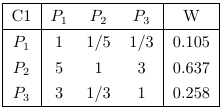
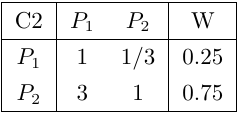
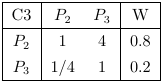
最后写出各方案即课程对选课层的层次总排序表
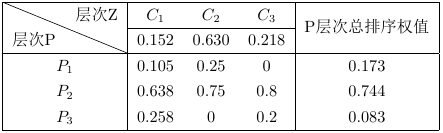
由于准则层各判断矩阵阶数分别为3,2,2,则由前表得RI值分别为0.58,0,0进行总排序一致性检验


从而CR=CI/RI=0.0332<0.1,满足一致性检验,所以课程A,B,C的权值分别为0.173,0.744,0.083,得最终选择课程B最优。从上述例子可以看出判断矩阵的构建很关键,要通过专家打分环节获得判断矩阵,一般通过经验判断、多人评审或参考文献等途径获得。
AHP源代码
clear;clc;
Z=[1 1/3 1/2;3 1 4;2 1/4 1]; %准则层C对目标层Z的判断矩阵
[CI0,Qz]=ahp(Z);
C1=[1 1/5 1/3;5 1 3;3 1/3 1];C2=[1 1/3;3 1];C3=[1 4;1/4 1];%方案层P对目标层Ci的判断矩阵
[CI1,Qc1]=ahp(C1);
[CI2,Qc2]=ahp(C2);
[CI3,Qc3]=ahp(C3);
%计算层次总排序权值
P1=Qz(1,1)*Qc1(1,1)+Qz(2,1)*Qc2(1,1)+Qz(3,1)*0;
P2=Qz(1,1)*Qc1(2,1)+Qz(2,1)*Qc2(2,1)+Qz(3,1)*Qc3(1,1);
P3=Qz(1,1)*Qc1(3,1)+Qz(2,1)*0+Qz(3,1)*Qc3(2,1);
%总排序一致性检验
CI=Qz(1,1)*CI1+Qz(2,1)*CI2+Qz(3,1)*CI3;
RI=Qz(1,1)*0.58+Qz(2,1)*0+Qz(3,1)*0;
CR=CI/RI;
if CR >=0.1
error('没有通过总排序一致性检验');
else
fprintf('通过总排序一致性检验n');
end
%% 通过判断矩阵求权值函数
function [CI,Q]=ahp(B)
%CI为一致性指数,Q为权值,B为判断矩阵
[n,m]=size(B);
%判别矩阵具有完全一致性
for i=1:n
for j=1:m
if B(i,j)*B(j,i)~=1
fprintf('i=%d,j=%d,B(i,j)=%d,B(j,i)=%dn',i,j,B(i,j),B(j,i));
error('判断矩阵不具有完全一致性');
end
end
end
%求特征值特征向量,找到最大特征值对应的特征向量
[V,D]=eig(B); %V是特征向量, D是由特征值构成的对角矩阵,A*V=V*D。
tz=max(D); %返回的行向量为矩阵每一列的最大值
tzz=max(tz); %返回行向量的最大值
c1=find(D==tzz); %find返回一个包含数组D中每个非零元素的线性索引的向量,由于D为对角矩阵这里返回值为tzz的索引。
tzx=V(:,c1);%特征向量
%权值
Q=zeros(n,1);
for i=1:n
Q(i,1)=tzx(i,1)/sum(tzx);
end
%计算权值还可以用算术平均法和几何平均法
%一致性检验
CI=(tzz-n)/(n-1);
RI=[0,0,0.58,0.9,1.12,1.24,1.32,1.41,1.45,1.49,1.52,1.54,1.56,1.58,1.59];
%判断是否通过一致性检验
CR=CI/RI(1,n);
if CR >=0.1
error('没有通过一致性检验');
else
fprintf('通过一致性检验n');
end
end
-
怎样分析一个网站的权重2011-04-19 3341
-
装备维修优化的决策分析2009-03-25 996
-
一种基于GiST的层次聚类算法2009-04-23 725
-
质量管理与决策分析学2010-01-29 678
-
基于比较可能度的属性权重未知的多属性决策方法2017-11-29 819
-
一种漏洞威胁基础评分指标权重分配方法2017-12-01 1151
-
一种多属性匹配决策方法2017-12-14 999
-
一种新的DEA公共权重生成方法2018-01-13 1155
-
一种层次结构中多维属性的可视化方法2018-01-14 896
-
一种约束权重的改进多目标跟踪方法2018-02-24 1075
-
一种基于用户偏好的权重搜索及告警选择方法2021-04-29 776
-
在 MATLAB 中实现层次分析法的主要步骤2023-06-12 3652
-
移动BI可视化分析助力决策分析应用2025-12-03 443
-
BI决策分析系统的关键组成部分:业务数据整合有何意义2025-12-18 44
全部0条评论

快来发表一下你的评论吧 !

