

Vivado中快速傅里叶变换FFT IP的配置及应用
电子说
描述
01
FFT简介
快速傅里叶变换 (Fast Fourier Transform,FFT), 即利用计算机计算离散傅里叶变换(DFT)的高效、快速计算方法的统称,简称FFT。DFT是实现了从频域(频域分析往往比时域分析更优越)对信号与系统进行分析。然而,随着序列长度的增加,计算量也显著增加,对于计算机而言,处理时间就越长,消耗的资源也就越多。
忘了什么是傅里叶变换的同学,赶紧拿出《信号与系统》翻一下。实在没书,找度娘。对于连续时间信号f(t),定义式如下:
傅里叶变换: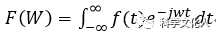
傅里叶逆变换: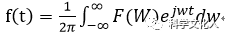
信号处理领域大名鼎鼎的傅里叶变换,正式由傅里叶提出的,不得不说,实在太伟大了,顶礼膜拜。
在信号处理中,由于计算机通常只能处理数字信号,因此通过对连续信号进行采样离散化,进而有了离散傅里叶变换。
话不多说,直入主题,首先把DFT公式搬出来:
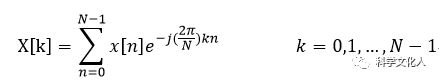
原信号x(t)的采样信号x[n]也可以用X[K]来表示:
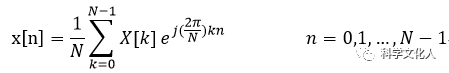
1965年,库利和图基提出了快速傅里叶变换(FFT)算法,采用这种算法能使计算机计算DFT所需要的乘法次数大为减少,特别是被变换的抽样点数N越多,FFT算法计算量的节省就越显著。
常用计算方法:
时间抽取算法:令序列的长度为N(2的幂),可以将时域序列x(n)分解为两部分,一是偶数部分x(2n),另一部分是计数部分x(2n+1),于是信号序列x(n)的离散傅里叶变换可以用两个N/2抽样点的离散傅里叶变换来辨识核计算。
频率抽取算法:按照频率吧抽取的FFT算法是将频域信号序列X(k)分解为奇偶两部分,但算法仍然是由时域信号序列开始逐级计算,同样把N点分成N/2点计算FFT。
02
FFT原理
FFT是DFT的快速算法,可以将一个信号从时域变换到频域。很多时候信号在时域很难进行信号特征分析,变换到频域后,就很容易看出信号的频率、功率、相位等特征信息。更多详细的解释,可移步看这里 深入浅出的讲解傅里叶变换(真正的通俗易懂) 或者在CSDN中阅读 深入浅出解释FFT系列(非公众号文章,超链接失败,抱歉,可去CSDN看原文博客) ,讲得比较清楚透彻,不愧是10年码龄的巨佬。在这里我就不再赘述了。
03
FFT IP Core使用
- 概述
以Xilinx Vivado设计套件中提供的FFT IP为例,简要说明如何进行FFT IP配置和设计。
FFT Core用于计算N点的DFT或IDFT,N=2m,m=3~16。对于计算FFT,有三种算术选项用于计算FFT:
- 全精度无缩放算法
- 定点缩放,提供缩放表
- 块浮点(运行时调整缩放)
对于N点大小,可对正向/逆向变换、缩放表循环前缀进行配置。
提供四种可选架构:
- Pipelined Streaming I/O
- Radix-4 Burst I/O
- Radix-2 Burst I/O
- Radix-2 Lite Burst I/O
端口描述
FFT IP Core的端口如图1所示,对端口的描述,参考产品指南PG-109-XFFT.pdf。
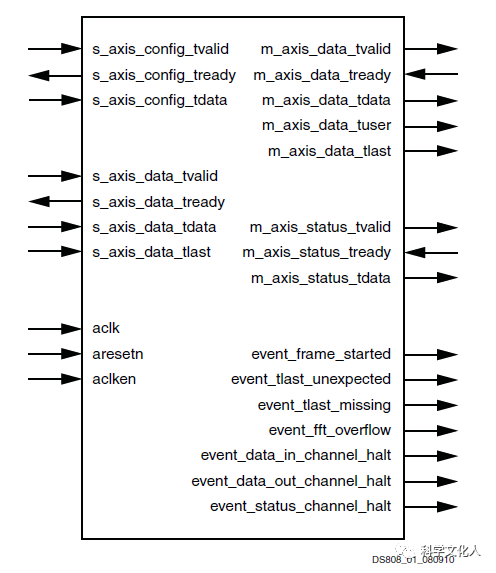
图1 FFT端口
- FFT IP配置
举个栗子:单通道,512点,Radix-2,Burst I/O,定点数,缩放,取整模式Truncation,输入数据位宽16bit,相位因子位宽16,自然序输出,无循环前缀。
在Vivado中创建工程后,在工程管理器下的IP Catalog中选择并配置FFT IP,在IP配置向导的指引下,依次进行相关参数的配置,如图2所示。配置通道数,变换长度,实现架构,数据格式,缩放,取整模式,数据呼出顺序,是否插入循环前缀(CP)等。
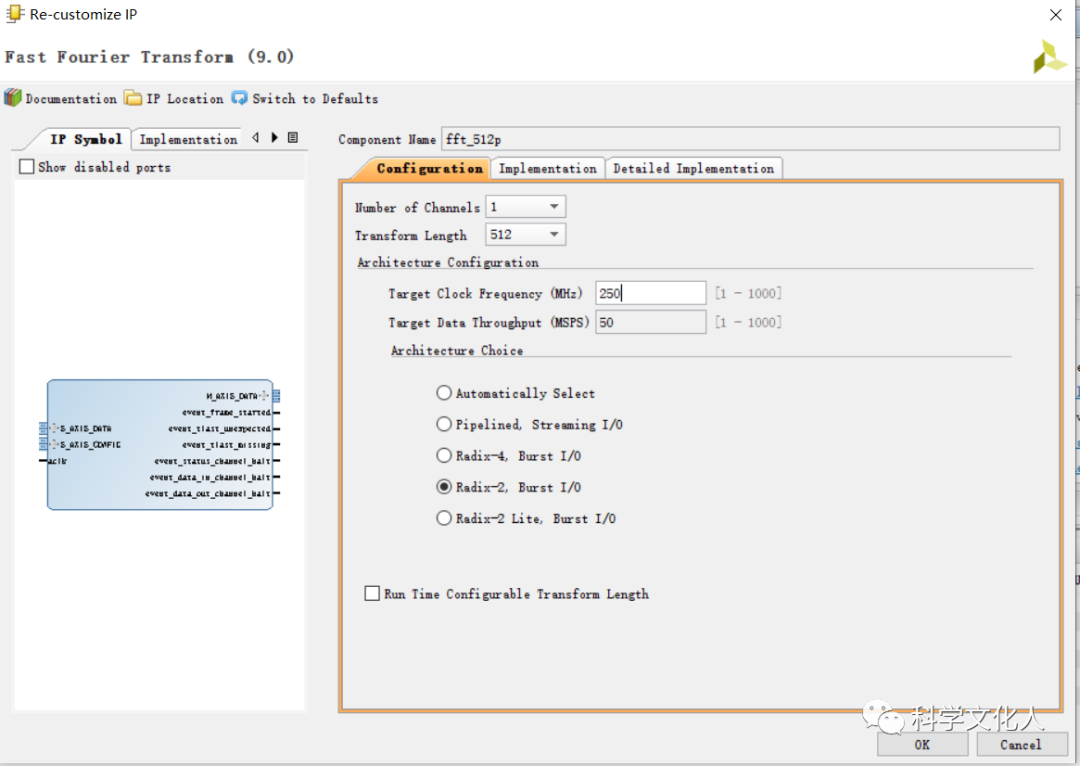
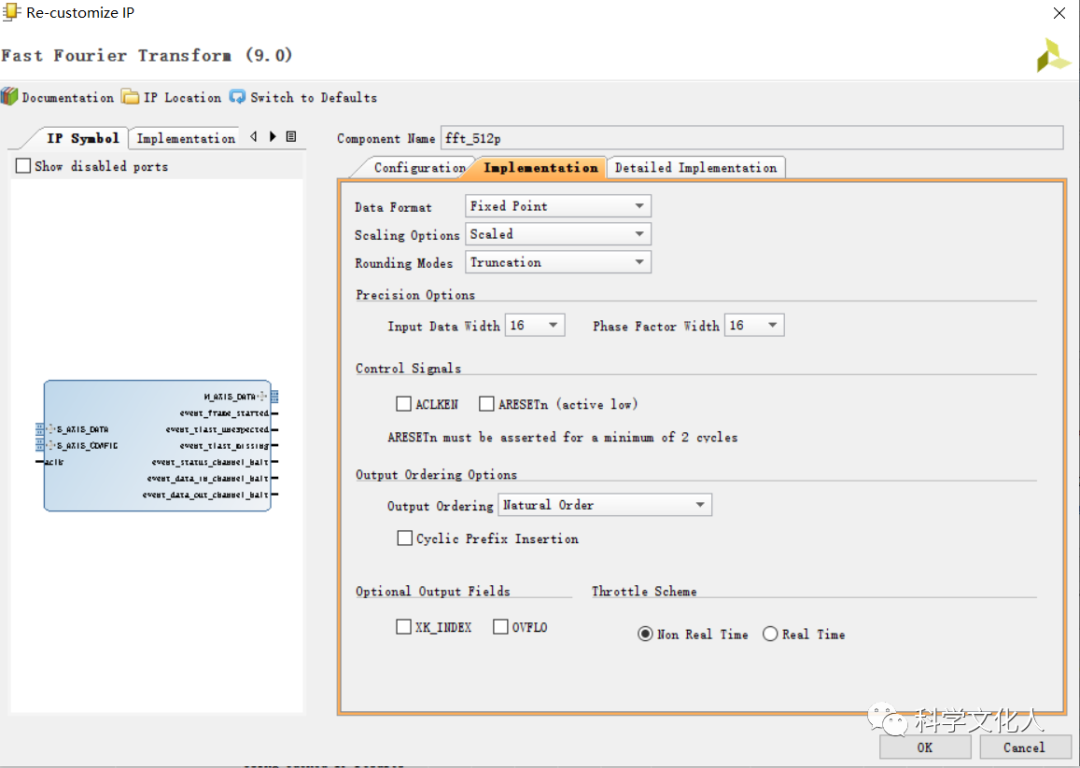
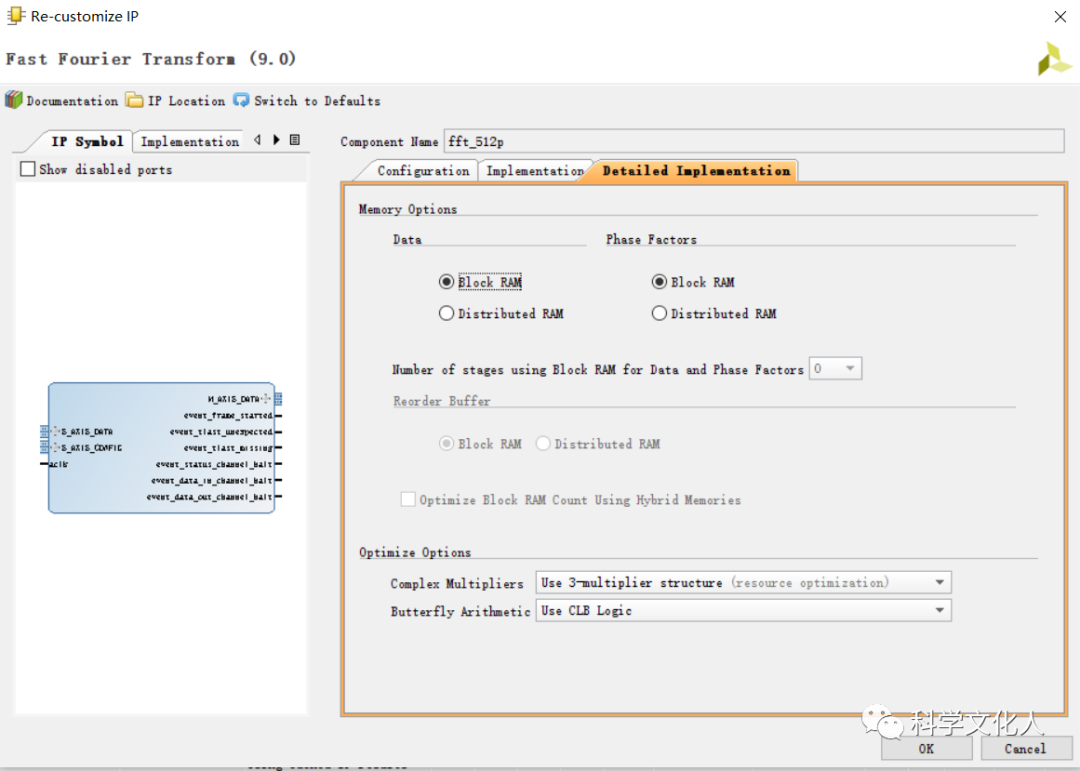
图2 FFT IP配置
在向导视图左侧,可查看IP端口框图,实现详情以及时延信息,如图3所示。这里需要注意输入输出数据的格式以及配置通道数据的格式。
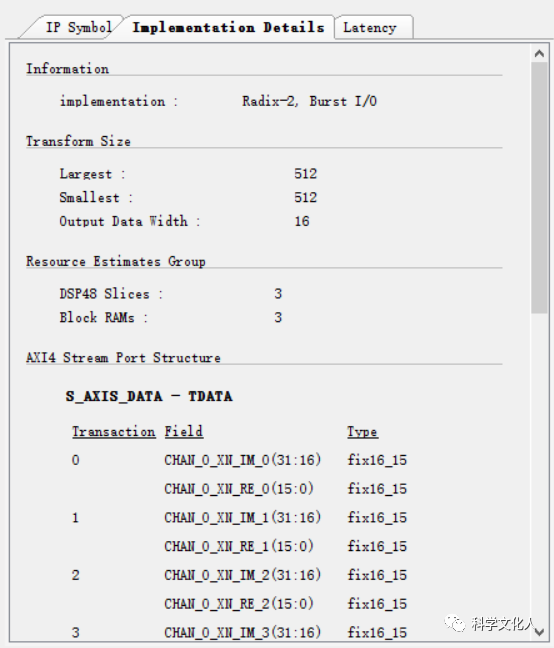
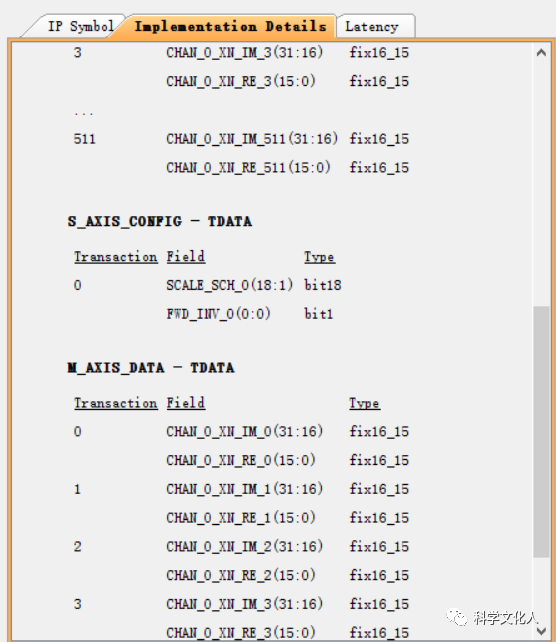
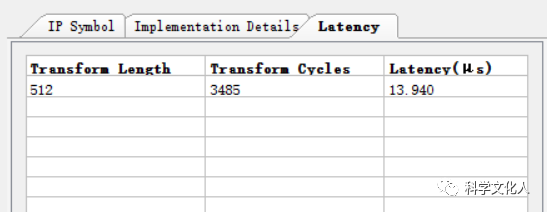
图3 查看IP实现信息
配置完成后,输出生成定制FFT IP,最后再将其实例化到工程模块中。
- AXI-Stream注意事项
该IP的端口采用了标准的AXI-Stream协议,数据传输基本握手,如图4所示。
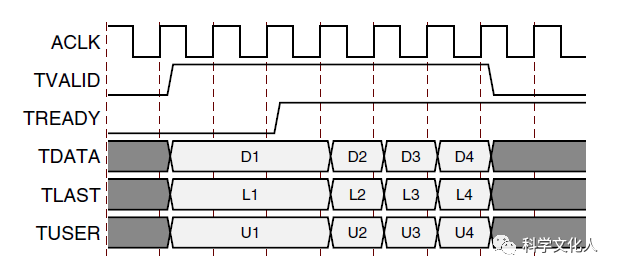
图4 AXI-Stream信道数据传输
- AXI信道规则
所有的TDATA和TUSER字段被打包成小端格式,也就是一个子字段的第0位与TDATA或TUSER的第0位对齐。
字段不包括在TDATA或TUSER中,除非以这种方式配置了核它需要字段出现。例如,如果核心配置为有一个固定的点大小,没有位分配给指定点大小的NFFT字段。
所有的TDATA和TUSER矢量都是8bit的整数倍。
- 配置通道
配置通道端口信号如表1所示。
表1 配置通道端口信号
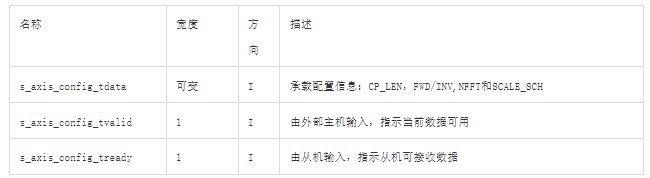
配置通道(s_axis_config)接口是AXI通道,TDATA字段接口定义如下表2所示,所有需要paded的字段如果未达到8bit边界,则需要扩展到8bit边界。扩展的bit可以未任意值,设计为常量值可节省器件资源。
表2 TDATA字段接口定义
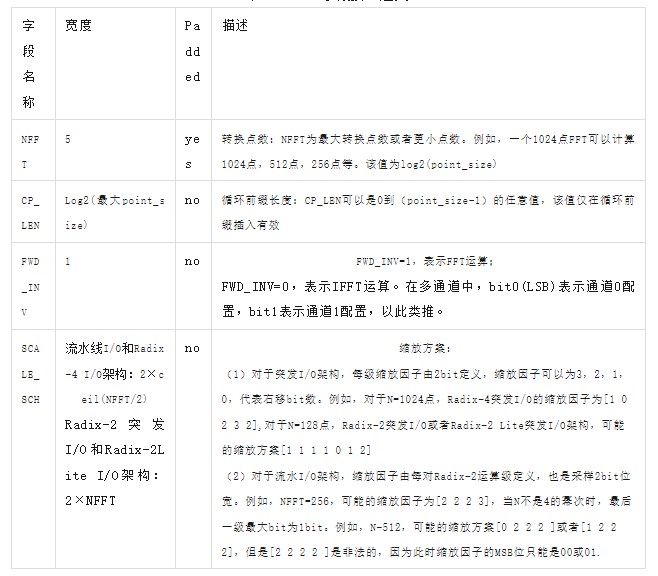
TDATA数据格式如图5所示。
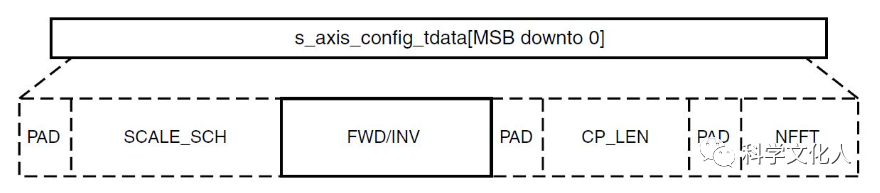
图5 config_tdata数据据格式
其中,NFFT设置情况,如表3所示。需要注意的是,如果选项runtime configurable transform length被选后,变换点大小才可以在配置通道的NFFT字段进行设置。
表3 NFFT设置
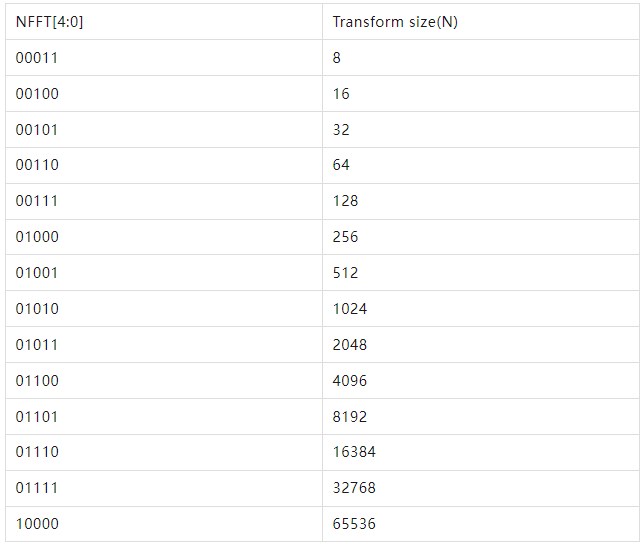
正反变换及缩放
FWD_INV=1时,正向变换;FWD_INV=0时,逆向变换。
对于FFT/IFFT各级缩放,在不同的实现架构中,缩放因子的设置有所不同。可参考表2 或者产品指南:PG109-xfft.pdf文档ch.4操作理论的Run Time Transform Configuration部分。
- 循环前缀(CP)
将输出结果的尾部复制到头部,输出顺序要选择自然序。插入循环前缀,可逐帧设置,不用打断帧处理进程。
- 补充:定点数
在FPGA处理过程中,常常要对浮点数进行定点化处理。Matlab中提供了一个非常方便的定点化函数fi。
fi(data,s,w,f) 各参数的定义:
s:signed or unsigned 标志;
signed: 包含符号位;
f:定点小数精度。
例如:在命令行输入fi(pi,1,16,13),回车,如图6所示。
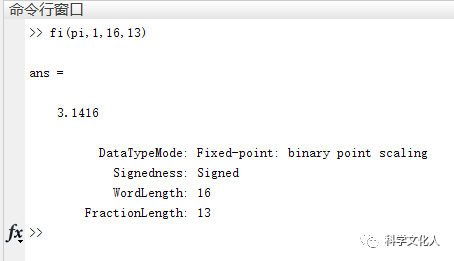
图6 浮点数定点
查看定点后的数据, 命令行输入ans.hex,显示十六进制数6488,如图7所示。
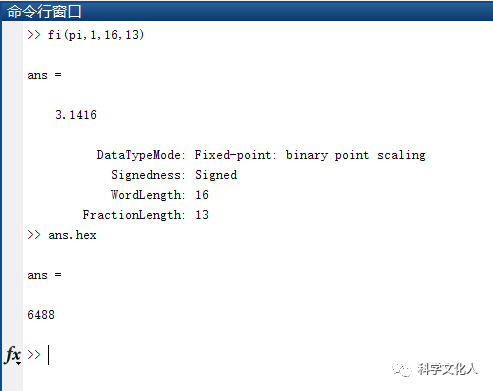
图7 定点16进制数据
命令行输入ans.dec,显示十进制数,如图8所示。
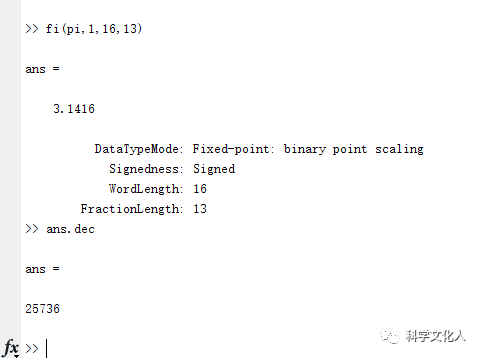
图8 定点10进制数据
在FPGA处理定点乘法,可用乘法器IP—Multiplier,如图9所示。
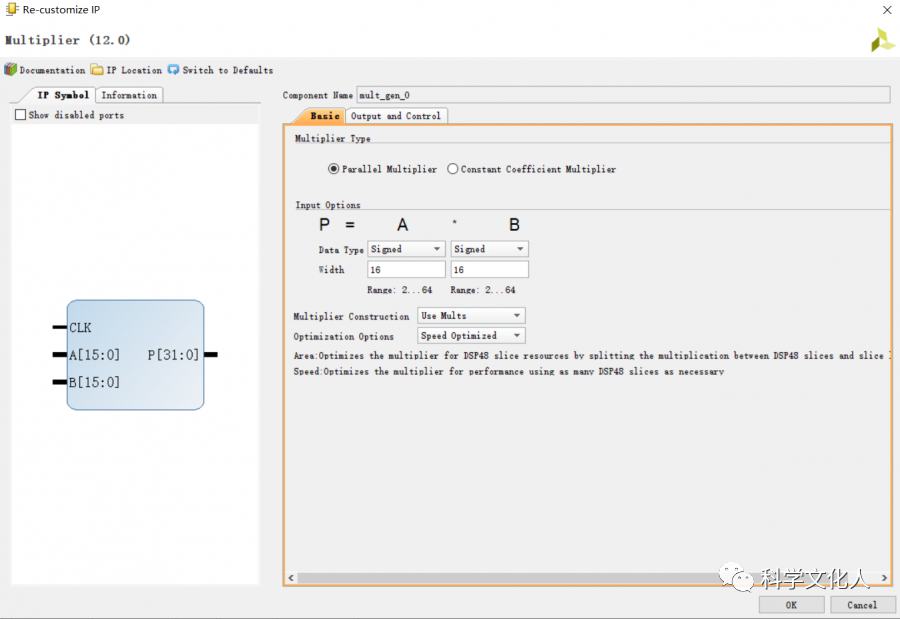
图9 乘法器IP
04
FFT模块设计demo
以调用FFT,并通过ROM预存所需数据进行一个简单的demo设计。
利用FFT IP,搭建工程。分别使用两个ROM存储DMRS0的I、Q两路数据,外部主机断言m_data_tready拉高时,准备开始从ROM读取数据,同时配置FFT。IFFT计算输出通过乘以一个系数,使其幅度值接近于1。设计框图如图10所示。
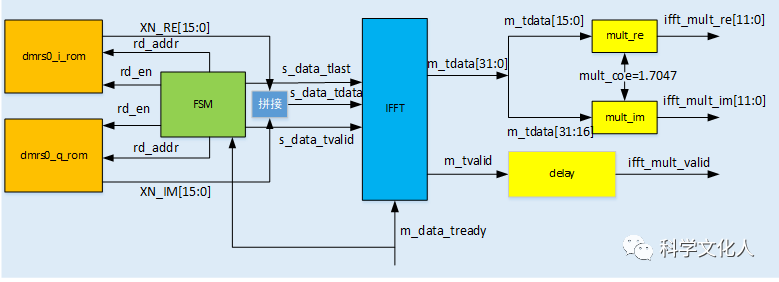
图10 设计框图
以DMRS0信号5M带宽300点(中间补零,至512点)作IFFT为例,创建工程,编写RTL代码。针对配置通道的数据配置(如SCALE_SCH、FWD/INV、CP_LEN、NFFT),假设基于Radix-2架构作IFFT,不加循环前缀,不更改NFFT点数,配置情况如下。
s_axis_config_tdata = 23'b0000_0000_0000_0000_0000_0000;
注意,高MSB五位做了填充,使得TDATA的位宽是8的整数倍。
FPGA仿真结果如图11所示。
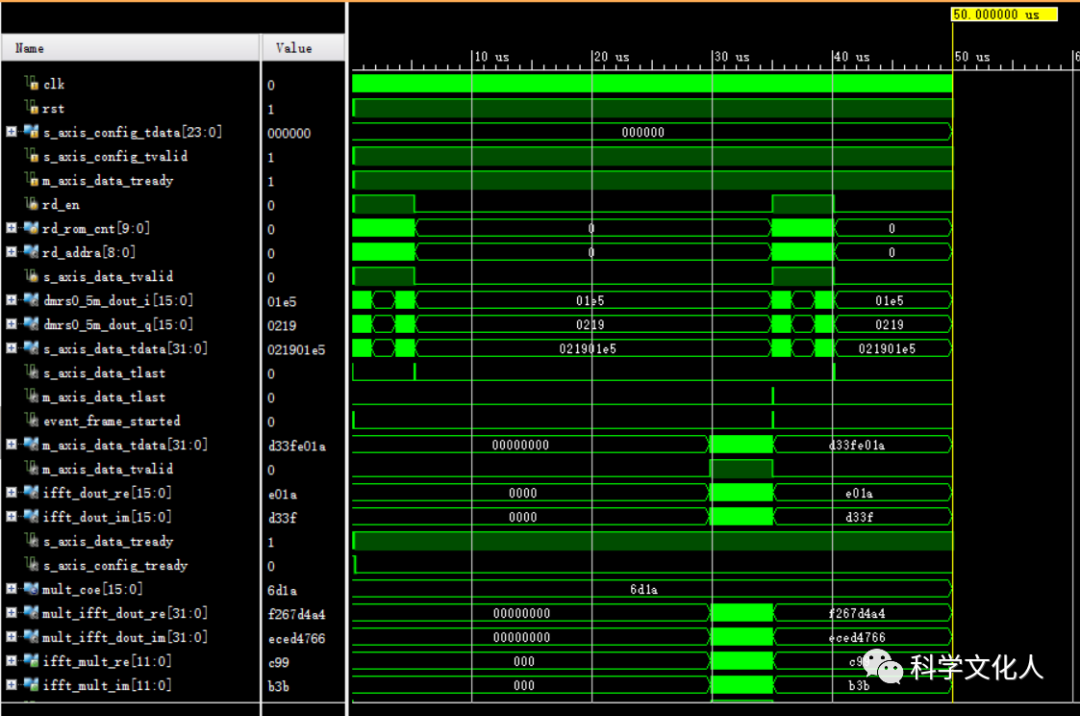
图11 FPGA工程仿真
MATLAB进行IFFT变换,并进行适当的缩放,同时将FPGA仿真的结果导入,计算各自的幅度,并绘于同一图中,如图12所示。
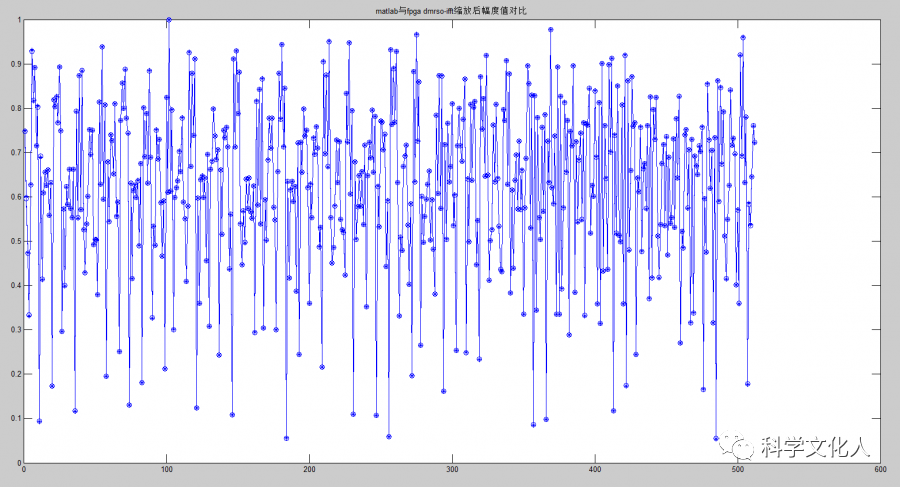
图12 幅度值对比
计算各自的相位角弧度,如图13所示。
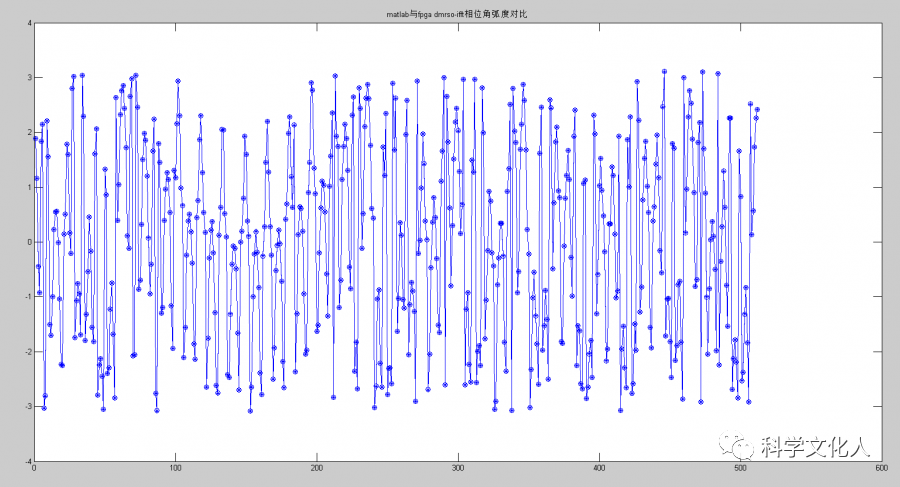
图13 相位弧度对比
通过对比分析可知,MATLAB仿真与FPGA实现结果基本一致。
在LTE、5G等无线通信中,IFFT和FFT变换是一个绕不过的话题。即便5G在探索非正交多址接入技术(NOMA),因主动引入干扰,接收机设计复杂度急剧上升,能否被采用不得而知。
-
经典傅里叶变换与快速傅里叶变换的区别2024-11-14 1947
-
Vivado中快速傅里叶变换IP配置及应用2022-07-22 2579
-
利用FFT算法实现快速傅里叶变换2022-07-10 4226
-
教大家在Vivado中FFT IP调配置及应用2021-07-23 7339
-
快速傅里叶变换FFT算法及其应用2020-05-28 2945
-
离散傅里叶变换(DFT)及其快速算法(FFT)2016-12-28 1065
-
快速傅里叶变换FFT的C程序代码实现2016-10-08 62842
-
详解快速傅里叶变换FFT算法2016-01-15 1919
-
FFT快速傅里叶变换2015-07-15 10516
-
FFT(快速傅里叶变换)运算器电路图2009-07-16 4956
全部0条评论

快来发表一下你的评论吧 !

