Matlab求解阶跃响应性能指标分析

1.定义

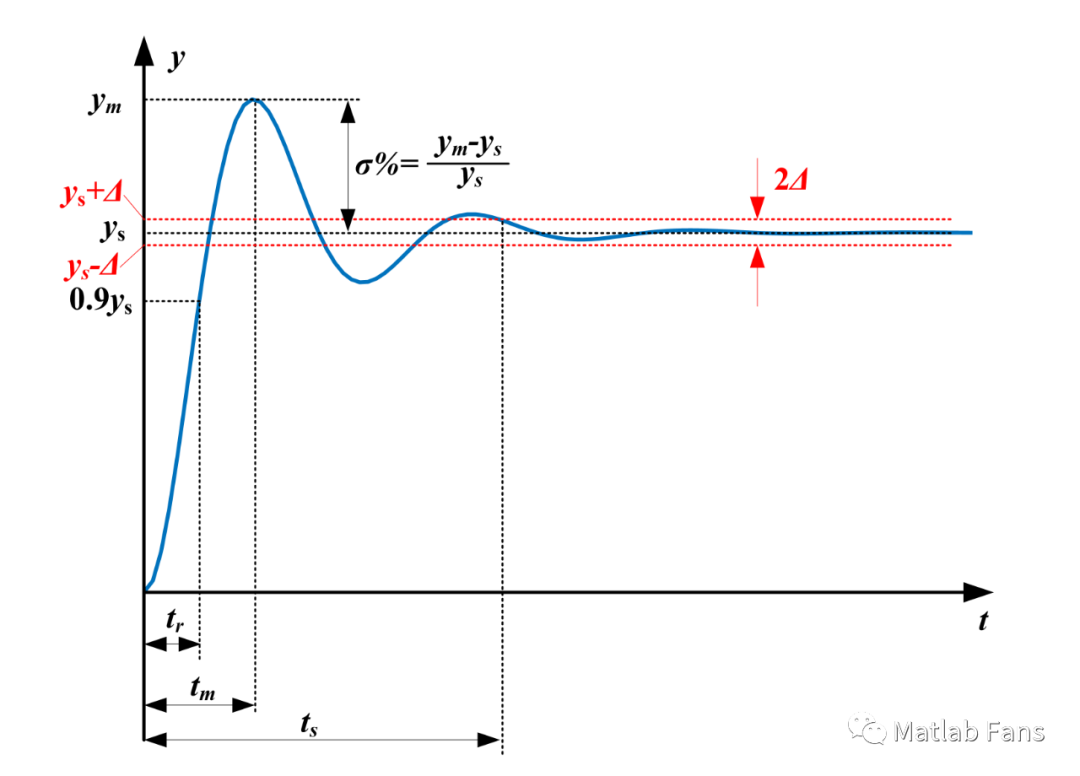
阶跃响应性能指标主要包括稳态值、上升时间、峰值时间和超调量，定义如下：

**稳态值ys**：当时间趋近于无穷大时，阶跃响应的输出值，ys=y(∞)。

** 上升时** 间tr ：输出阶跃响应达到90%稳态值时所对应的时刻。

**峰值时间tm** ：输出阶跃响应峰值ym所对应的时刻。

** 超调量σ** ：输出阶跃响应峰值ym与稳态值ys之差所占稳态值ys的百分比, σ%= (ym-ys)/ys。

** 调整时间ts** ：输出阶跃响应进入稳态值ys±Δ误差带范围内所对应的时刻, 一般取Δ=0.02或Δ=0.05。

2. 函数

按照阶跃响应性能指标的定义，笔者使用Matlab开发了函数 Fun_Step_Performance.m ，使用数值算法求出各类阶跃响应的性能指标值，函数简单、易用、通用性好。

function [ys,tr,ts,tm,ov] = Fun_Step_Performance(t,y,drawflag)
% [ys,tr,ts,ov] = Fun_Step_Performance(t,y) 标准阶跃响应的性能指标求解
% 本程序适用于标准阶跃响应曲线，末尾时间必须已经接近稳态值
% t-y 为阶跃响应的时间-输出配对序列，可由[y,t] = step(sys)求得
% drawflag为时候作图标志，不输入或输入非0值时，默认作图，输入0时不做图
% ys 稳态值
% tr 上升时间，默认为0-90%的上升时间
% ts 调整时间，默认为2%的调整时间
% tm 为峰值时间
% ov 超调量 %
% e.g.
%  sys = tf(1,[1 2*0.5*1 1]);
%  [y,t] = step(sys,15);
%  [ys,tr,ts,tm,ov] = Fun_Step_Performance(t,y,1);

3. 演示

**3.1 **一阶系统阶跃响应性能指标

% Eg 1 一阶系统
sys = tf(1,[3 1]);
[y,t] = step(sys,25);
[ys,tr,ts,tm,ov] = Fun_Step_Performance(t,y);

%% 阶跃响应指标结果：

上升时间：7s

调整时间：11.5s

峰值时间：25s , 超调量：0%

稳态值：1

%% 阶跃响应指标结果显示结束

**3.2 **求复杂系统阶跃响应性能指标

% 5阶系统
sys = tf(1,[1 2*0.20*1 1]) * tf(1,[2 1]) * tf([1.5 1],[1 2*0.25*3 9]); 
[y,t] = step(sys,35);
[ys,tr,ts,tm,ov] = Fun_Step_Performance(t,y);

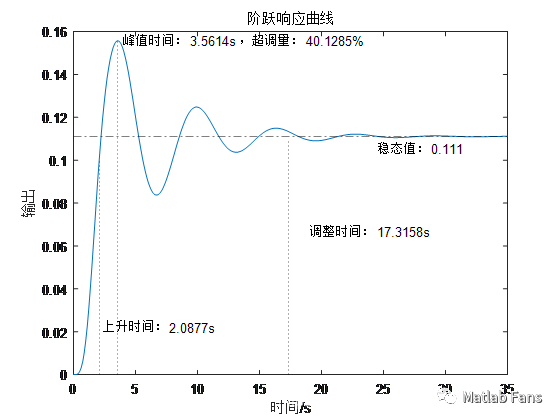
%% 阶跃响应指标结果：

上升时间：2.0877s

调整时间：17.3158s

峰值时间：3.5614s，超调量：40.1285%

稳态值：0.111

%% 阶跃响应指标结果显示结束

**3.3 **不同阻尼比时二阶系统的阶跃响应性能指标

% Eg 3 求解不同阻尼比时二阶系统的阶跃响应特性
wn = 1;    % 固有频率
kes_vet = [0.2 0.4 0.6 0.8 1 1.2];   % 阻尼比序列
figure
hold on
for ii = 1:length(kes_vet)
    kes = kes_vet(ii);
    sys = tf(1,[1 2*kes*wn wn^2]);   % 二阶系统传递函数
    [y,t] = step(sys,50);            % 阶跃响应
    [ys(ii),tr(ii),ts(ii),tm(ii),ov(ii)] = Fun_Step_Performance(t,y,0);  % 求解阶跃响应,不绘图
    plot(t,y)
    Str{ii} = [ 'xi = '  num2str(kes)];
end
legend(Str)
xlabel('时间t/s')
ylabel('输出响应y')

tr =

1.8349    2.0737    2.4540    2.9954    4.0000    4.9407

ts =

19.2661 8.2949 5.8282 3.6866 5.5000 7.9051

tm =

3.2110    3.4562    3.9877    5.1843   40.0000   50.0000

ov =

52.6622 25.3725 9.4610 1.5144 0 0

对于二阶系统，阻尼比的变化不影响输出稳态值，随着阻尼比增加，上升时间逐步增大、调整时间先减小再增大、峰值时间逐步变大、超调量逐步变小；当阻尼比在0.707左右时，上升时间和调整时间较快，且超调量很小，系统综合性能较好，工程上通常设计阻尼比在0.707左右，称之为最佳阻尼比。