OFDM-MSK-LFM雷达通信一体化信号性能分析

  一、前言

现代电子战对频谱资源利用越来越多，致使系统复杂性越来越高、电磁干扰愈来愈严重，因此部分学者提出了雷达通信一体化系统，旨在高效的使用频谱资源，降低设备复杂度。雷达通信一体化信号的优化设计是其重点研究方向，本文主要研究典型一体化信号OFDM-MSK-LFM。雷达通信一体化技术是雷达信号与通信信号复合而成的，设计的基本要求是要考虑雷达与通信性能的均衡，因此无论是雷达信号还是通信信号，均需要合理的选择，本文考虑频谱利用率选择OFDM信号，考虑雷达传输的恒包络要求，选择MSK调制技术与LFM雷达信号。

  二、OFDM-MSK-LFM一体化信号模型

2.1 MSK调制原理

由于在前述两篇文章OFDM-16QAM-LFM与OFDM-BPSK-LFM中已经介绍了OFDM-LFM系列一体化信号模型，在此我们就不过多赘述，需要了解的同学可以查看对应的文章，也可以参考文末参考文献。

MSK信号具有恒定的信息包络且每两个码元之间相位不会跳变，占用带宽也较小，将其与OFDM-LFM信号相结合可得到一体化信号。

   MSK 信号的第k 个码元可以表示为

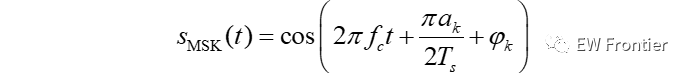
式中：ak为第k个输入码元，取值为±1； φk为第个码元的相位常数，在时间kTs＜t≤(k+1)Ts内保持不变，其作用是在t=kTs处保持相位连续。

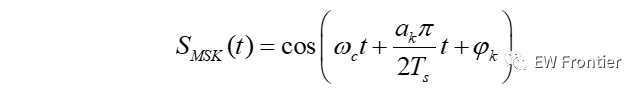
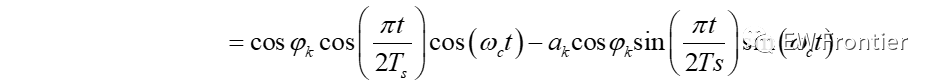
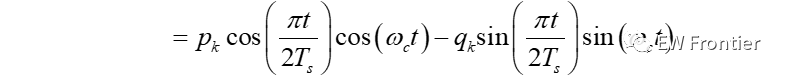
MSK调制原理如下图所示，基带码元先差分编码，然后经过串并转换分成I、Q两路，再与对应的载波相乘，然后再相加完成MSK的调制。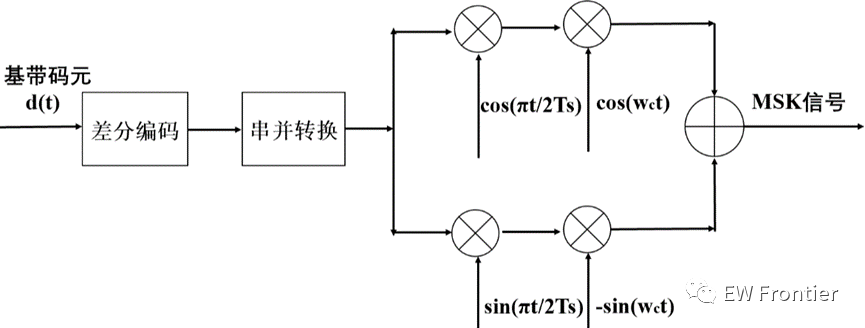

图1 MSK调制信号生成过程

2.2OFDM-MSK-LFM一体化信号

结合OFDM-LFM 技术得到一体化波形公式推导为

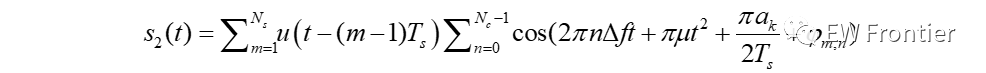
  三、仿真分析

参数设置：OFDM：采样率100Mhz，载波数2；LFM：带宽40Mhz，脉宽12us，载频10Mhz；MSK：载频4Khz。

3.1 MSK调制

根据图2和图3不难看出，MSK信号具有良好的恒包络性，这一特性能够使其在雷达探测过程中保持良好感知能力，同时不会影响模糊函数，与此同时MSK加入了调制数据，进一步实现通信与感知的并存。观察图3，可以发现MSK信号的频谱主要集中与两个频率，具有较高的频带利用率，这也满足雷达通信一体化的基本要求。基于上述条件，可以发现MSK调制是一种适合用于雷达通信一体化技术的调制方式。

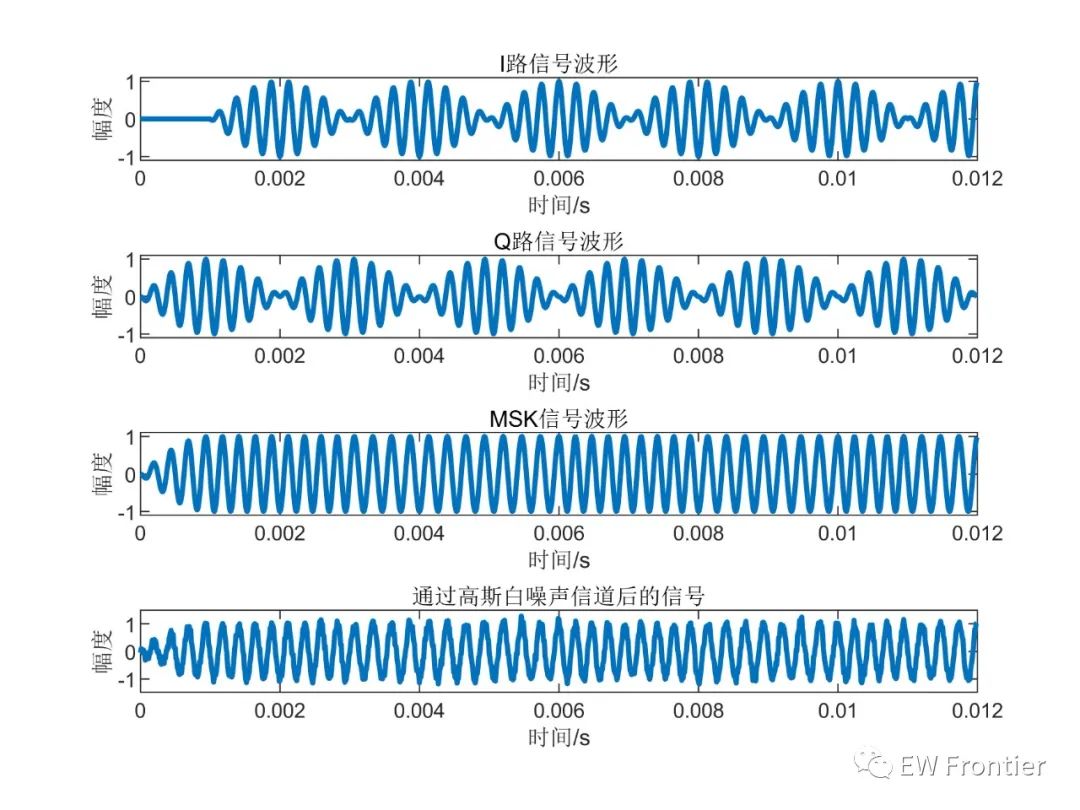图2 MSK信号时域波形

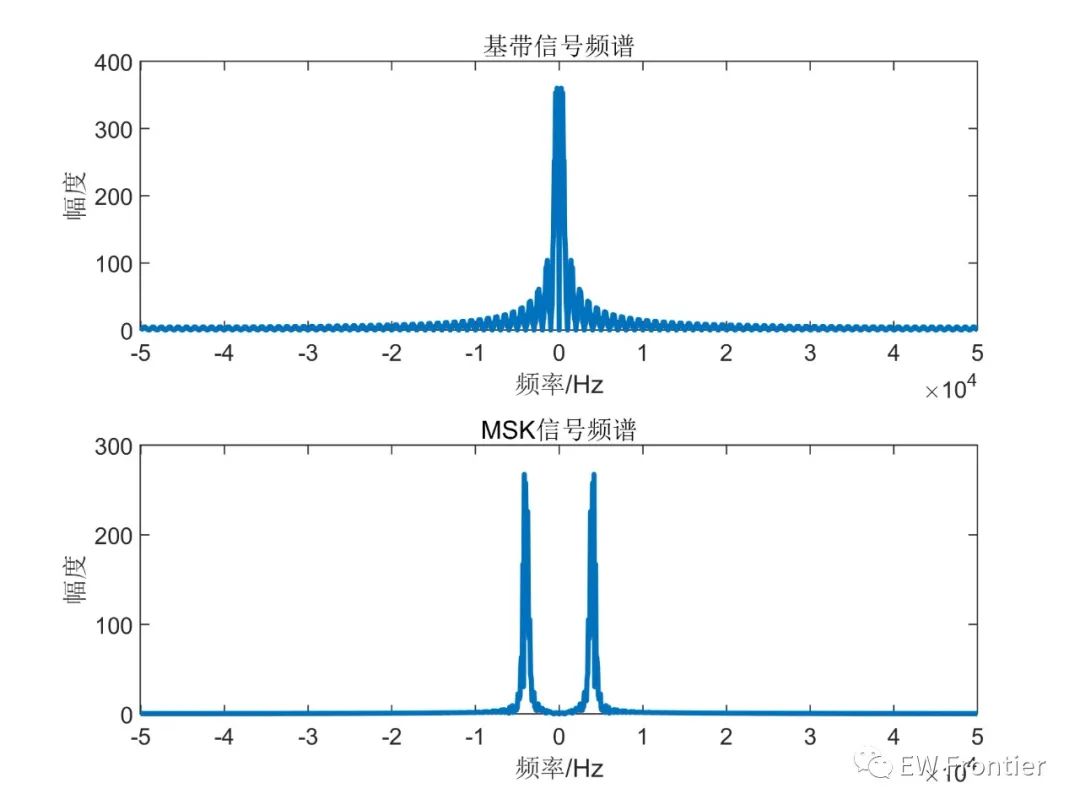
图3 MSK信号频谱

3.2 OFDM-MSK-LFM模糊函数

图4-图6分别是OFDMMSK-LFM的模糊函数三维视图、速度切片与距离切片，看过之前OFDM-16QAM-LFM与OFDM-BPSK-LFM两篇文章的同学应该能够发现MSK调制令一体化信号的模糊函数更趋于图钉形状，具有较低的旁瓣，因此其雷达探测能力得到很好的保证，而OFDM-MSK-LFM信号的通信误码率取决于MSK调制，在文末参考文献中有相应的介绍，其通信可靠性较高。

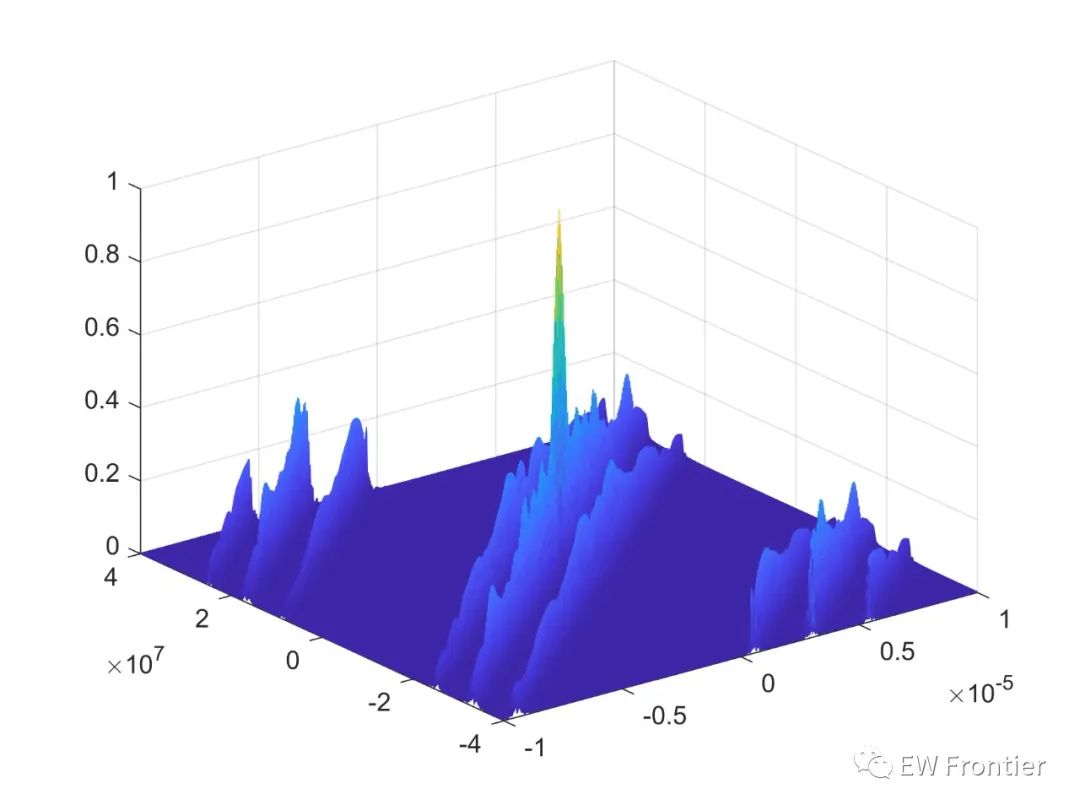
图4 OFDM-MSK-LFM模糊函数三维图

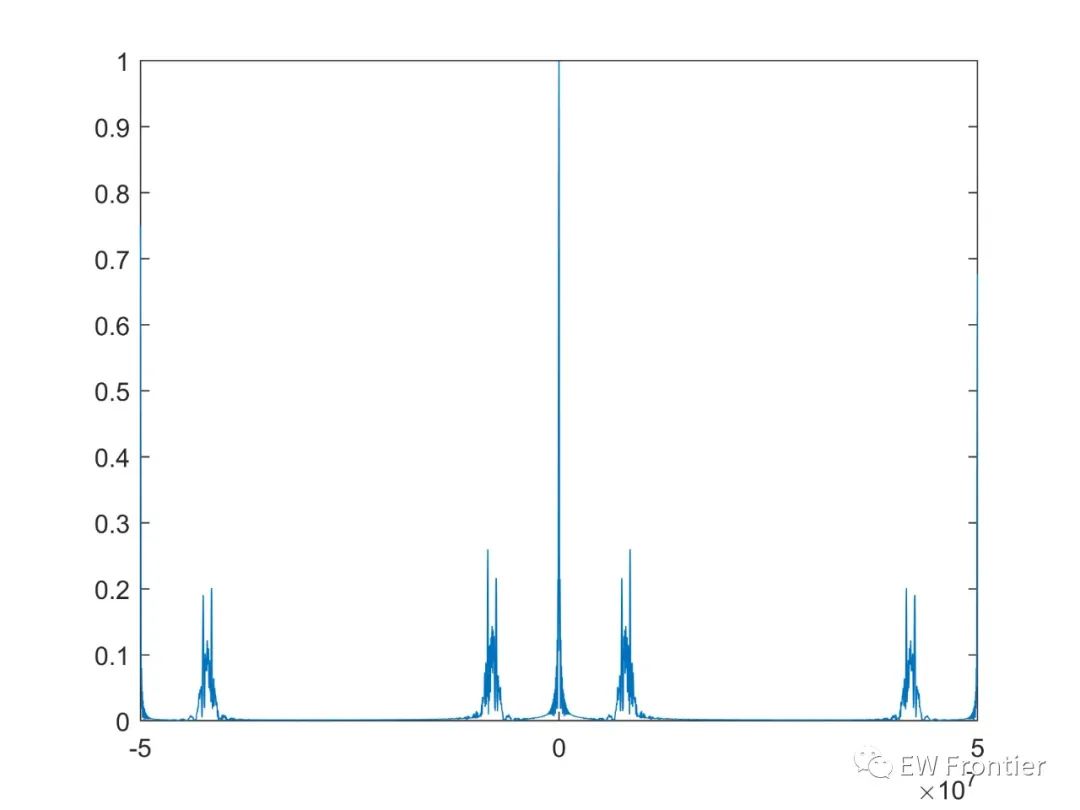图5 OFDM-MSK-LFM零多普勒

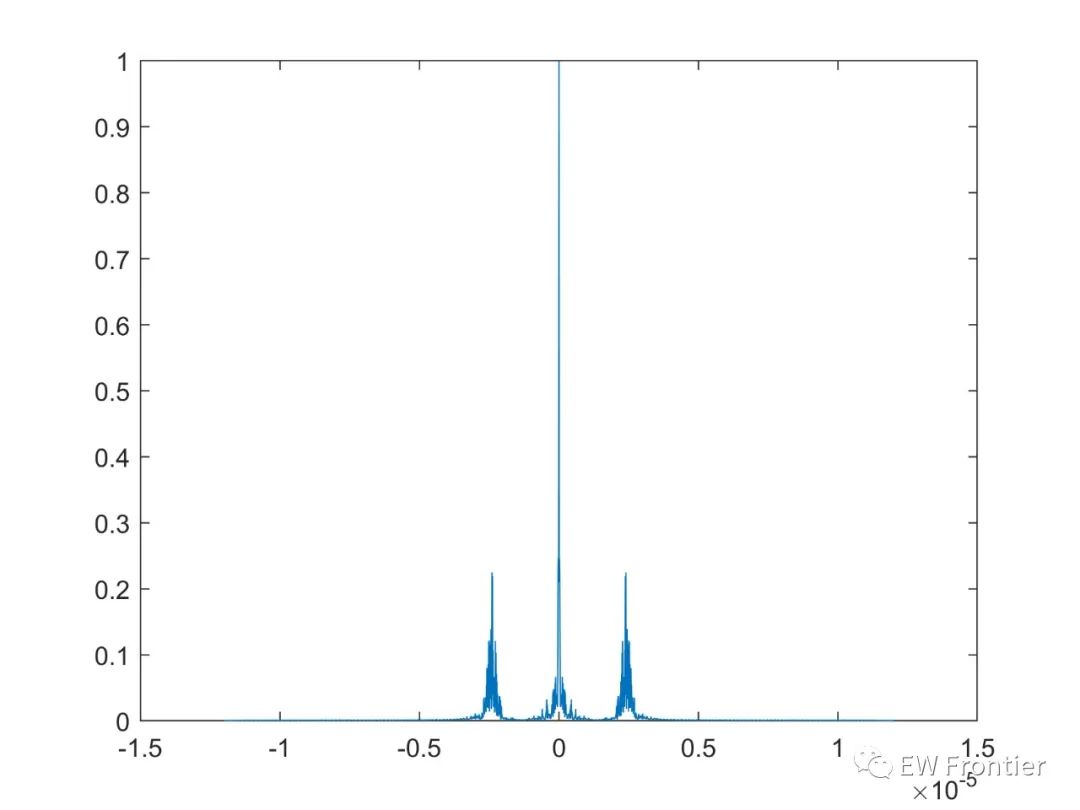
图5 OFDM-MSK-LFM零时延

  四、总结

雷达通信一体化技术需要良好的通信信号、雷达信号以及调制方式，这三者共同决定了一体化信号的雷达探测性能与通信性能，因此本文将OFDM、LFM与MSK三种技术相结合，主要利用了OFDM的频谱利用率、信息传输速率，LFM的良好探测性能，MSK携带调制信息能够保证恒包络性，不影响雷达探测。

其实雷达通信一体化信号设计最简单的就是这类组合优化设计，希望本文对相关研究的同学能有帮助。        参考文献

[1]肖博, 霍凯, 刘永祥. 雷达通信一体化研究现状与发展趋势[J]. 电子与信息学报, 2019, 41(3): 739–750.

[2] 赵忠凯，石妙. 基于OFDM-LFM 的雷达通信一体化波形设计[J].应用科技,2021,48(3):73-77.

 

OFDM-MSK-LFM一体化信号代码详见：https://mbd.pub/o/myCreated
学术交流Q群：479772742
MSK调制代码：
clear all;                  % 清除所有变量
close all;                  % 关闭所有窗口
clc;                        % 清屏
%% 基本参数
M=11;                       % 产生码元数    
L=100;                      % 每码元复制L次,每个码元采样次数
Ts=0.001;                   % 每个码元的宽度,即码元的持续时间
Rb=1/Ts;                    % 码元速率1K
dt=Ts/L;                    % 采样间隔
TotalT=M*Ts;                % 绝对码总时间
t=0TotalT-dt;           % 时间1
TotalT2=(M+1)*Ts;           % 相对码总时间
t2=0TotalT2-dt;         % 时间2
Fs=1/dt;                    % 采样间隔的倒数即采样频率


%% 产生单极性波形
wave=randi([0,1],1,M);      % 产生二进制随机码,M为码元个数


%% 绝对码变相对码
wave2=ones(1,M+1);          % 产生1*(M+1)的全1行向量
%% 相对码第一个参考值为1，相对码b(n+1)=绝对码a(n)和相对码b(n)做异或
for  k = 2:M+1
    wave2(k) = xor(wave(k-1),wave2(k-1));%生成相对码
end
fz=ones(1,L);               % 定义复制的次数L,L为每码元的采样点数
x1=wave(fz,:);              % 将原来wave的第一行复制L次，称为L*M的矩阵
juedui=reshape(x1,1,L*M);   % 将刚得到的L*M矩阵，按列重新排列形成1*(L*M)的矩阵
x2=wave2(fz,:);             % 将原来wave2的第一行复制L次，称为L*(M+1)的矩阵
jidai=reshape(x2,1,L*(M+1));% 将刚得到的L*(M+1)矩阵，按列重新排列形成1*(L*(M+1))的矩阵


%% 单极性变为双极性
% 基带信号变为双极性即jidai为1的时候，jidai为1;jidai为0的时候，jidai为-1
for n=1:length(jidai)
    if jidai(n)==1
        jidai(n)=1;
    else
        jidai(n)=-1;
    end
end


%% 产生I、Q两路码元
I_lu=wave2(1end);        % 相对码的奇数位置为I路码元
Q_lu=wave2(2end);        % 相对码的偶数位置为Q路码元


%% I、Q两路单极性码元变为双极性码元
I_lu=2*I_lu-1;
Q_lu=2*Q_lu-1;


%%I、Q两路码元的单个码元的持续时间是原始码元中单个码元的两倍,Tb=2Ts，并且I路码元延时Ts
fz2=ones(1,2*L);            % 定义复制的次数2L
x3=I_lu(fz2,:);             % 将原来I_lu的第一行复制2L次，称为2L*((M+1)/2)的矩阵
I=reshape(x3,1,(2*L)*((M+1)/2));% 将刚得到的2L*((M+1)/2)矩阵，按列重新排列形成1*(2L*((M+1)/2))的矩阵
x4=Q_lu(fz2,:);             % 将原来Q_lu的第一行复制2L次，称为2L*((M+1)/2)的矩阵
Q=reshape(x4,1,(2*L)*((M+1)/2));% 将刚得到的2L*((M+1)/2)矩阵，按列重新排列形成1*(2L*((M+1)/2))的矩阵
I_yanshi=zeros(1,length(I));% 产生1*length(I)的零向量
% I路延时Ts，即I路1至L置零，原来1至(2*L)*((M+1)/2)-L的数移动到L+1至最后
I_yanshi(L+1:end)=I(1:(2*L)*((M+1)/2)-L);


%% 绘制码元波形
figure(1);                  % 绘制第1幅图
subplot(411);               % 窗口分割成4*1的，当前是第1个子图 
plot(t,juedui,'LineWidth',2);% 绘制绝对码元波形，线宽为2
title('绝对码信号波形');    % 标题
xlabel('时间/s');           % x轴标签
ylabel('幅度');             % y轴标签
axis([0,TotalT,-1.1,1.1])   % 坐标范围限制


subplot(412);               % 窗口分割成4*1的，当前是第2个子图 
plot(t2,jidai,'LineWidth',2);% 绘制相对码元波形，线宽为2
title('相对码信号波形');    % 标题
xlabel('时间/s');           % x轴标签
ylabel('幅度');             % y轴标签
axis([0,TotalT2,-1.1,1.1])  % 坐标范围限制


subplot(413);               % 窗口分割成4*1的，当前是第3个子图 
plot(t2,I,'LineWidth',2);   % 绘制I路码元波形，线宽为2
title('I路信号波形');       % 标题
xlabel('时间/s');           % x轴标签
ylabel('幅度');             % y轴标签
axis([0,TotalT2,-1.1,1.1])  % 坐标范围限制


subplot(414);               % 窗口分割成4*1的，当前是第4个子图 
plot(t2,Q,'LineWidth',2);   % 绘制Q路码元波形，线宽为2
title('Q路信号波形');       % 标题
xlabel('时间/s');           % x轴标签
ylabel('幅度');             % y轴标签
axis([0,TotalT2,-1.1,1.1])  % 坐标范围限制
%% MSK调制
fc1=4000;                   % 载波1频率4kHz   
fc2=1/(4*Ts);               % 载波2频率1/(4*Ts)  
zb1=cos(2*pi*fc1*t2);       % 同相载波1
zb2=-sin(2*pi*fc1*t2);      % 正交载波1
zb3=cos(2*pi*fc2*t2);       % 同相载波2
zb4=sin(2*pi*fc2*t2);       % 正交载波2
I_wave=I_yanshi.*zb1;             
I_wave=I_wave.*zb3;         % I路波形
Q_wave=Q.*zb2;       
Q_wave=Q_wave.*zb4;         % Q路波形
msk=I_wave+Q_wave;          % MSK的调制 
figure(2);                  % 绘制第2幅图
subplot(411)                % 窗口分割成4*1的，当前是第1个子图 
plot(t2,I_wave,'LineWidth',2);% 绘制I路信号的波形 
title('I路信号波形')        % 标题
axis([0,TotalT2,-1.1,1.1]); % 坐标范围限制
xlabel('时间/s');           % x轴标签
ylabel('幅度');             % y轴标签


subplot(412)                % 窗口分割成4*1的，当前是第2个子图 
plot(t2,Q_wave,'LineWidth',2);% 绘制Q路信号的波形 
title('Q路信号波形')        % 标题
axis([0,TotalT2,-1.1,1.1]); % 坐标范围限制
xlabel('时间/s');           % x轴标签
ylabel('幅度');             % y轴标签


subplot(413)                % 窗口分割成4*1的，当前是第3个子图 
plot(t2,msk,'LineWidth',2); % 绘制MSK的波形 
title('MSK信号波形')        % 标题
axis([0,TotalT2,-1.1,1.1]); % 坐标范围限制
xlabel('时间/s');           % x轴标签
ylabel('幅度');             % y轴标签

 

　　审核编辑：汤梓红