电感和电容器的工作原理，电容器电感器计算公式

电感器可以想象为电容器的对立面。电容器和电感器之间的主要区别在于电容器在其极板之间携带保护性电介质，从而抑制电流在其端子上的传导。在这里，它就像一个开路。

另一方面，电感器的电感通常（尽管并非总是）具有极低或最小的电阻。它本质上表现得像一个闭合电路。

电容器电感器二元性

在电子学中存在一个独特的术语，用于电路的两个参数或电路的一部分之间的这种类型的关系。这种类型的对的元素被称为彼此的对偶。例如，根据传导电流的能力，开路是闭合电路的对偶。

根据相同的原理，电感器是电容器的双通道。电感器和电容器的双重性比传导电流的自然能力要深得多。

本文比较了电感和电容器的工作原理，并通过计算和公式对结果进行了评估。

尽管电感器通常很少出现在电子电路中，因为今天它主要被有源滤波器中的运算放大器所取代），但电路中涉及的其他部分似乎带有一定量的电感。

电容器或电阻器端子的自感在高频电路中成为一个大问题，这就解释了为什么无引线表面贴装电阻器和电容器在此类应用中如此频繁地使用。

基本电容器方程

电容器的基本方程是定义法拉的公式：

C = Q / U ［等式 19］

其中 C 是以法拉为单位的电容，Q 是以库仑为单位的电荷，U 是以伏特为单位的板之间的 pd。

通过方程19，我们得到一个形式的公式 Q = ∫ I dt + c，其中c是初始电荷（如果可用）。确定 Q 后，我们能够从方程 19 中确定
U：

U = 1 / C ∫ I dt + c/ C ［等式21］

电容器的一个重要特性是这样的，如果对其施加周期性电流（通常是正弦振荡的电流），电容器上的电荷和两端的电压也会正弦波动。

电荷或电压曲线是负余弦曲线，或者我们可以将其想象为一条正弦曲线，它落后于电流曲线 π/2 rad （90°）。

定义亨利（电感单位）的基本方程为

L = NΦ / I ［等式 22］

参考单个线圈，亨利的自感可以是单位电流通过时的磁通量关系（韦伯中的磁通量《1）乘以绕组N的数量（因为磁通量穿过每一圈）（I = 1
A）。使用诺依曼方程可以从方程22中提取出一个更方便的定义。这声称：

U = N （dΦ / dt） ［方程23］

该方程表明，电感内感应的e.m.f.相对于磁通量的链接变化率。

通量变化越快，感应e.m.f越高。例如，当电感器或线圈上的磁通量以 2 mWb s 的速率上升时-1，假设线圈有二十五圈，则 U = 25x2 =
50V。

e.m.f.的路径使其能够抵抗楞次定律所概述的通量变化。

这个真理通常是通过在等式右侧前面加上减号来指出的，但是只要我们相信 U 是后面的 e.m.f.，就可以删除该符号。

差异

方程23中的术语dΦ / dt表示我们学到的通量变化率。这个短语被称为 Φ 相对于 t
的微分，整个算术分支都致力于处理这种表达式。该短语的形式是单个数字 （dΦ） 除以另一个数量 （dt）。

微分用于关联许多比例集：例如，dy/dx将变量x和y关联起来。当使用横轴上的 x 值和垂直轴上的 y 值绘制图形时，dy/dx
表示图形的斜率或梯度有多陡。

如果U是FET栅源电压，其中T是相关的漏极电流，则dI/dU表示I在给定U变化时变化的量。在讨论电感时，dΦ
/dt可以是磁通量随时间的变化率。

计算微分可以被视为积分的逆过程。本文没有足够的空间来研究微分理论，但是我们将定义一个常用量及其微分的表格。

标准差速器

上表的工作原理是使用 I 和 t 作为因子，而不是例程 x 和 y。因此，它的细节与电子产品特别相关。

例如，考虑到 I= 3t +2，I 相对于时间的偏差方式可以在图 的图形中可视化。38. 为了找到 I 在任何时候的变化率，我们参考表格估算
dI/dt。

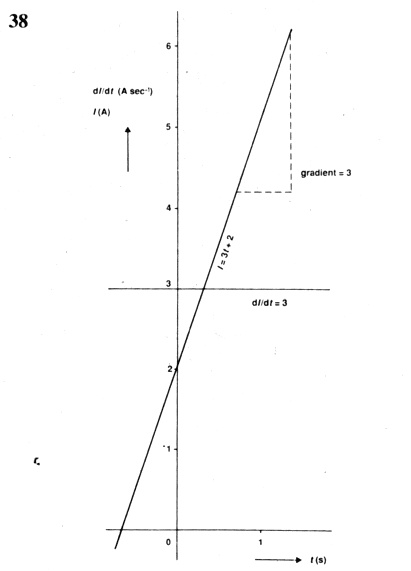
函数中的第一个元素是 3t，或者，将其格式化为表的第一行，3t1.Ifn = 1，差分为 3t1-1= 3吨0.

由于 t0= 1，差分为 3。

第二个量是2，可以表示为2t0.

这会改变 n = 0，并且微分的大小为零。常数的差分将始终为零。将两者结合起来，我们有：

dI / dt = 3

在此图中，差分不包括 t，这意味着差分不依赖于时间。

简单地说，图中曲线的斜率或梯度。38 是 3 一直连续。下面的图 39 显示了不同函数的曲线，I = 4 sin 1.5t。

参考表格，此函数中的 α = 1.5 和 b = 0。该表显示，dl/dt = 4x1.5cos1.5t = 6cos 1.5t。

这告诉我们I的瞬时变化率。例如，在 t = 0.4 时，dI/dt = 6cos0.6 = 4.95。这可以在图中看到。如图39所示，其中6
cos0.6t的曲线包括t=4.95时的值0.4。

我们还可以观察到，当 t = 4.1 时，曲线 5sin4.95t 的斜率为 0.4，如该点与曲线的切线所示（相对于两个轴上的不同刻度）。

当t = π/3时，电流处于最高和恒定的点，在这种情况下，dI/dt = 6cos（1.5xπ/3）：0，对应于电流的零变化。

相反，当t = 2π/3并且电流以最高可能的水平从正电平切换到负值时，dI/dt = 6cosπ =
-6，我们看到它的最高负值，表现出很高的电流减少。

微分的简单好处是，它们允许我们确定与I = 4sin 1.5t相比复杂得多的函数的变化率，而无需绘制曲线。

返回计算

通过重新组织方程 22 中的项，我们得到：

Φ = （L / N）i ［方程24］

其中 L 和 N 具有恒定的维度，但 Φ 和 I 可能具有相对于时间的值。

在时间方面区分等式的两边可以得到：

dΦ / dt = （L / N）（dI / dt） ［公式 25］

将此等式与方程 23 合并得到：

U = N（L/N）（dI / dt） = L （dI / dt） ［等式26］

这是表达亨利的另一种方式。我们可以说，线圈的自感为1 H，电流变化为1 A s-1产生 1 V
的反电流。给定一个定义电流如何随时间变化的函数，方程26帮助我们计算电感在任何时刻的背面e.m.f.。

以下是一些示例。

A） I= 3（恒定电流为 3 A）;dl/dt = 0。您找不到任何电流变化，因此背面 e.m.f. 为零。

B） I = 2t（斜坡电流）;dI/dt = 2 A s-1.当线圈承载L = 0.25 H时，背面e.m.f.将恒定在0.25x2 = 0.5
V。

C） I = 4sin1.5t（上图中给出的正弦电流;dl/dt = 6cos 1.5t。给定一个 L = 0.1 H 的线圈，瞬时回 e.m.f.
为 0.6cos1.5t。背面e.m.f.遵循图的差分曲线。39，但幅度为0.6 V而不是6 A。

理解“对偶”

以下两个等式分别表示电容器和电感器的等式：

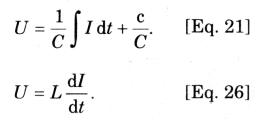
它帮助我们确定组件上产生的电压水平，根据特定功能随时间变化的电流。

让我们评估通过区分方程 21 的 L 和 H 侧相对于时间获得的结果。

dU / dt = （1 / C）I

众所周知，微分是积分的逆，∫I dt 的微分反转积分，结果只有 i。

区分 c/C 会给出零，重新排列项会产生以下内容：

I = C.dU / dt ［等式27］

这使我们能够知道电流的方向，无论它是流向电容器还是从电容器流出，以响应根据给定函数变化的电压。

有趣的是，上述电容器电流方程看起来类似于电感的电压方程（26），它表现出电容，电感的二元性。

同样，当应用于电容器和电感器时，电流和电位差（pd）或电流和pd的变化率可以是双的。

现在，让我们对方程 26 与时间进行积分，以完成方程四分：

∫ U dt+c = LI

dI/dt 的积分是 = I，我们重新排列表达式得到：

I = 1/L∫ U dt + e/L

这看起来与方程21非常相似，进一步证明了电容和电感的双重性质，以及它们的pd和电流。

到目前为止，我们有一组四个方程，可用于解决电容器和电感器相关问题。

例如，方程 27 可以应用于解决问题，如下所示：

问题：施加在100uF上的电压脉冲产生如下图所示的曲线。

这可以使用以下分段函数进行定义。

计算流过电容器的电流并绘制相应的图表。

溶液：

对于第一阶段，我们应用等式27

I = C（dU / dt） = 0

对于 U 可能以恒定速率上升的第二个实例：

I = C（dU / dt） = 3C = 300μA

这显示了恒定的充电电流。

对于 U 以指数方式下降的第三阶段：

这表明电流以指数递减的速率从电容器流出。

相位关系

在abobe图中，一个交替的pd施加到电感器上。此 pd 在任何时刻都可以表示为：

其中 Uo 是 pd 的峰值。如果我们以环路的形式分析电路，并顺时针方向应用基尔霍夫电压定律，我们得到：

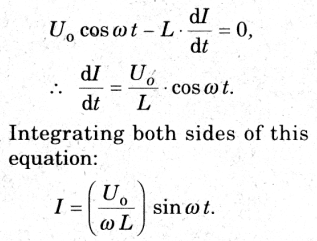
但是，由于这里的电流是正弦的，括号中的项的值必须等于峰值电流Io，因此我们最终得到：

如果我们比较方程29和等式30，我们发现电流I和电压你的频率相同，I落后U π/2。

生成的曲线可以在下图中进行研究：

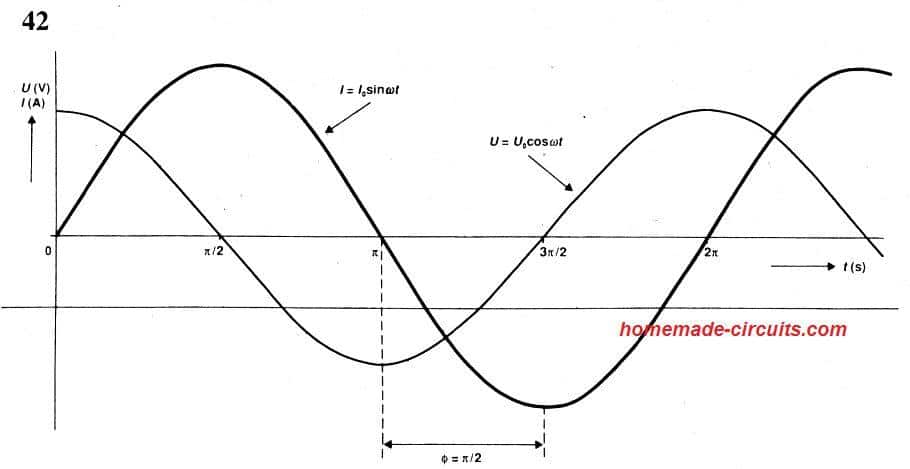
C

由此可见电容器和电感器之间的对比关系。对于电感，电流滞后电位差π/2，而对于电容器，电流领先于pd。这再次表明了这两个组成部分的双重性质。