

如何计算修正的正弦波形值?
描述
我相信您可能经常想知道如何实现优化和计算修正方波的正确方法,以便在逆变器应用中使用时产生几乎相同的正弦波复制。
本文中讨论的计算将帮助您学习将修改后的方波电路转换为正弦波等效的技术。
实现此目的的第一个标准是将修改后的正方形的RMS值与正弦波对应物相匹配,以使结果尽可能接近地复制正弦波形。
什么是RMS(均方根)
我们知道,我们家用交流正弦波形电压的均方根是通过求解以下关系来确定的:
V峰值 = √2 Vrms
其中V峰值是正弦波形周期的最大极限或峰值极限,而波形每个周期的平均幅度显示为Vrms
公式中的√2帮助我们找到交流周期的平均值或净值,其电压随时间呈指数变化。由于正弦电压值随时间变化并且是时间的函数,因此不能使用基本平均公式来计算,而是依赖于上述公式。
或者,交流有效值可以理解为相当于直流电(DC)的值,当连接在阻性负载上时,直流电(DC)产生相同的平均功耗。
好了,现在我们知道了计算正弦波周期的RMS的公式,参考其峰值电压值。
这也可以用于评估我们家用 50 Hz AC 的峰值和
RMS。通过解决这个问题,我们得到所有基于220V的电源交流系统的RMS为310V,峰值为220V。
计算修正方波有效值和峰值
现在让我们看看如何将这种关系应用于改进的方波逆变器中,以便为220V系统设置正确的波形周期,这对应于220V AC正弦等效。
我们已经知道,交流有效值相当于直流波形的平均功率。这给了我们这个简单的表达:
V峰值 = Vrms
但是我们也希望方波的峰值在310V,所以上面的方程似乎不成立,不能用于目的。
标准是每个方波周期的峰值为310V,RMS或平均值为220V。
为了正确解决这个问题,我们借助方波的开/关时间或占空比百分比,如下所述:
50 Hz 交流波形的每个半周期的持续时间为 10 毫秒 (ms)。
修改后的半波周期最粗糙的形式必须如下图所示:
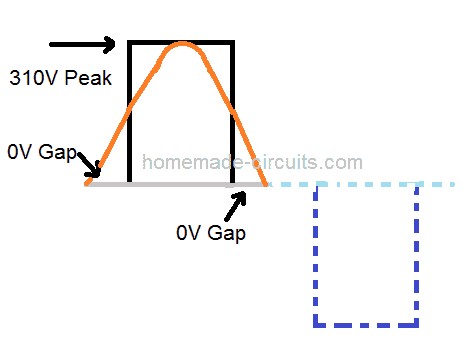
我们可以看到,每个周期从零或空白间隙开始,然后脉冲高达310V峰值脉冲,再次以0V间隙结束,然后重复该过程另一个半周期。
为了达到所需的220V RMS,我们必须计算和优化峰值和零间隙部分或周期的ON/OFF周期,以使平均值产生所需的220V。
灰线表示周期的 50% 周期,即 10 毫秒。
现在我们需要找出开/关时间的比例,这将产生平均220V。我们这样做是这样的:
大约 220 / 310 x 100 = 71 %
这表明,上述修改周期中的310V峰值应占71 ms周期的10%,而两个零间隙应为29%的组合,即各占14.5%。
因此,在10 ms的长度中,第一个零点部分应为1.4 ms,然后是310 V峰值,持续7 ms,最后是另一个1.4 ms的最后一个零间隙。
一旦完成,我们可以期望逆变器的输出产生相当好的正弦波形复制。
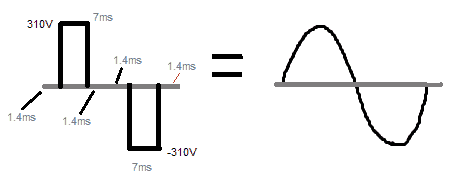
尽管如此,您可能会发现输出并不是正弦波的理想复制品,因为所讨论的修正方波是最基本的形式或粗略类型。如果我们希望输出以最大精度匹配正弦波,那么我们必须采用
SPWM 方法。
我希望上面的讨论可能对您如何计算和优化用于复制正弦波输出的修改正方形有所启发。
为了进行实际验证,读者可以尝试将上述技术应用于这个简单的修改后的逆变器电路。
-
示波器测量正弦波波形的基本步骤2024-05-27 5375
-
正弦波逆变器和修正波逆变器的区别2024-02-01 8918
-
纯正弦波逆变器和修正弦波逆变器的区别2024-01-23 12290
-
什么是方波、矩形波、修正正弦波、纯正弦波?方波怎样变成正弦波?2023-10-25 9078
-
什么是方波、矩形波、修正正弦波、纯正弦波?2023-06-10 21302
-
有源晶振的波形是正弦波吗?怎么测量?2023-04-17 3841
-
纯正弦波逆变器、修正弦波逆变器和方波逆变器介绍2022-04-16 6893
-
产生正弦波形需送DA的数据是如何计算的2021-07-15 1630
-
正弦波所需的DAC数据是如何计算的2021-07-14 2402
-
电源技术之正弦波形(二)2020-09-18 5472
-
正弦波逆变器制作过程详解2019-10-30 21719
-
纯正弦波逆变器哪个好_纯正弦波逆变器排行榜2018-03-13 96605
-
什么是正弦波逆变器_正弦波逆变器的工作原理及相关电路图2017-11-20 89987
-
Labview之不同扫描方式显示正弦波形2016-04-19 773
全部0条评论

快来发表一下你的评论吧 !

