

运放的频率响应和环路稳定性分析
模拟技术
描述
上一篇《运放(一)......》是从静态的角度去讨论运放的一些特性,默认电路的反应速度足够快,不需要考虑信号传输和建立的过程。这一篇主要讨论运放对不同频率信号的行为,讨论因信号延迟给反馈环路带来的问题,以及相应的解决方法。
在《运放(一)......》中说到,运放总是根据两个输入端之间的电压偏差去重新调整输出,输出电压又通过分压电路引回到反相输入端,最终使得两个输入端电压相等。换句话说:运放总是在检测输出电压,根据输出和目标之间的偏差重新调整输出,直到与目标输出电压相等。如果仔细思考这个过程,会发现可能出现以下问题,导致输出电压一直在目标值左右振荡:信号从输入端经过放大环节到输出端,再经过反馈环节回到输入端,这个过程通常会有延迟。因此,运放无法及时得知当前的输入能得到什么样的输出,如果调整力度过大或者延迟比较严重,输出电压就容易调过头。等会发现调过头了,又试着纠正回来,如此往复......如果情况不是很严重,每次调过头的量都比上一次的小,那么输出会振荡几次后稳定下来,这种情况叫振铃(如图1)。如果延迟比较严重、调节力度又比较大,每次都无法及时收手,最终输出会在目标值左右一直振荡,停不下来,这就是自激振荡。
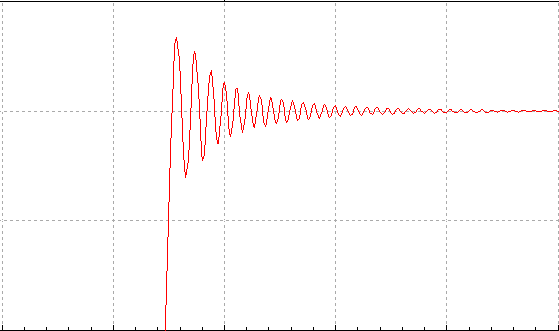
图1 输出振铃
从时域到频域
前面是从时域的角度来简单说明自激振荡的原因,虽然直观,却不方便定量分析,下面是从频域的角度描述:随着频率升高,运放的输出电压(Uo)相对差分输入电压(Up-Un)会有相位滞后,记为φA,相位滞后其实就是以信号周期为参考的时间延迟。同时,运放的开环增益A也会随频率增大而减小。另外,如果反馈电路不是纯电阻,反馈电压(Uf)相对输出电压(Uo)也可能有相位滞后,记为φF。通常用正数表示相位超前,负数表示相位滞后,比如说φ=-90°,表示相位滞后90°,后面这两种表述会混着用。
如果信号经过放大环节和反馈环节总的相位滞后达到180°(φA+φF=-180°),说明反馈回来的信号反相了。本来反馈回来的信号是要从输入信号(Ui)中减掉的,剩下的才是真正输入运放的信号(Un=Uf,Up=Ui,Uo=A·(Up-Un))。现在反馈回来的信号反相了,减去一个相位相反的信号,相当于加上那个未经反相的信号。也就是说输入信号经过放大环节和反馈环节绕一圈回来,在两个输入端之间产生的电压与原本的差分输入相位相同,可以代替原本的输入信号,负反馈变成了正反馈(如图2、图3)。如果此时反馈信号比原本的差分输入信号幅度还大,那这个信号将会在由运放和反馈电路组成的环路中绕圈一次又一次地被放大,最终在电源电压的限制下或电路中其它非线性因素限制下稳定幅度,这就是自激振荡。如果反馈回来的信号比原本的差分输入信号幅度小,那这个信号在环路中每绕一圈将被衰减一次,最终消失,就表现为输出电压在目标值左右振荡几次后稳定下来,这种情况就是振铃。上面说的总相位滞后180°,有时也说滞后360°,其实是一样的意思,因为负反馈本身也可以看成相移180°。

图2 反馈信号没有相移

图3 反馈信号滞后180°
信号经过放大环节和反馈环节绕一圈回来与原本差分输入信号的大小关系称为环路增益,与原本差分输入信号的相位关系称为环路相移,这两个东西是判断环路稳定性的关键。环路增益包括运放的开环增益和反馈系数两部分,开环增益用A表示、反馈系数用F表示,两者的乘积AF就是环路增益,AF=Uf/Ud(Ud=Up-Un)。开环增益A=Uo/Ud,是运放在没有引入反馈时本身的放大倍数,Uo相对Ud的相移为φA。反馈系数F=Uf/Uo(Un=Uf),表示取输出电压多大比例的一部分反馈到输入,Uf相对Uo的相移为φF。因为反馈电路就是对输出电压分压,所以F总是小于等于1。差分输入信号Ud被放大A倍得到Uo,又从中取比例为F的一部分反馈到反相输入端,所以AF就表示反馈回来的信号与原本差分输入信号的倍数关系。比如AF>1,说明信号绕一圈回来比原本的差分输入还大。

图4 反馈电路框图
总结说,自激振荡要满足两个条件:1、放大环节和反馈环节的总相位滞后达到180°,反馈回到两个输入端之间的信号与原本的差分输入信号同相,可以代替原本的输入信号。2、环路增益大于或等于1,即反馈回来的信号不能比原本的差分输入信号小,否则信号最终将衰减为零。相应的,抑制自激振荡的方法就是破环以上两个条件中的一个。比如:减小环路带宽,在环路相位滞后达到180°前将环路增益衰减到1倍以下;或者引入环路的相位超前补偿,使得环路增益衰减到1倍时总相位滞后小于180°。换个更直观的说法:要解决自激振荡,要么调节的力度不要太大;要么对输出的变化趋势有个预判,提前做出反应。通过改变环路的频率响应来提高环路稳定性称为频率补偿,关于这部分后面再具体讨论。为了更好地描述这部分内容,这里先引入极点和零点的概念,并分别讨论运放和反馈电路的频率响应,最后才是频率补偿。
极点和零点
从传递函数的角度讨论极点和零点过于抽象,而且我也搞不懂那些东西,这里从幅频特性和相频特性的角度讨论。
幅频特性和相频特性如图5所示的频率点称为极点,最常见的极点由RC低通滤波电路产生,如图6。在极点处,幅度降低3dB,并在此之后每10倍频降低20dB,即频率每升高10倍幅度变为原来的1/10。如果将幅频特性曲线折线化,则极点处斜率-1(减1)。相位上,在极点处输出信号相对输入信号滞后45°,在极点的十倍频之后趋于90°,并最终停留在90°。
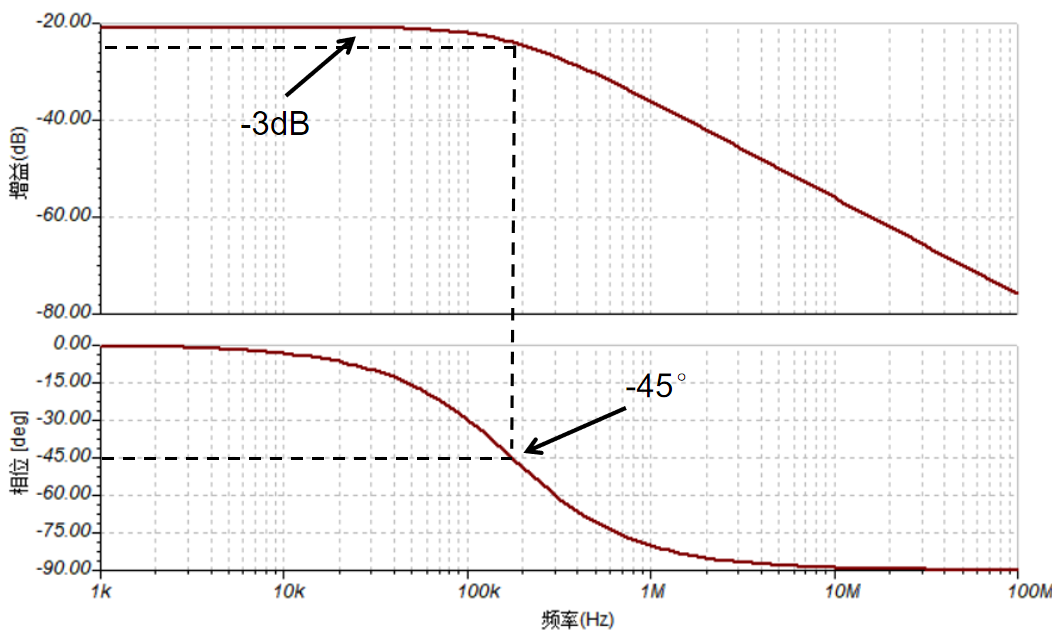
图5 极点波特图
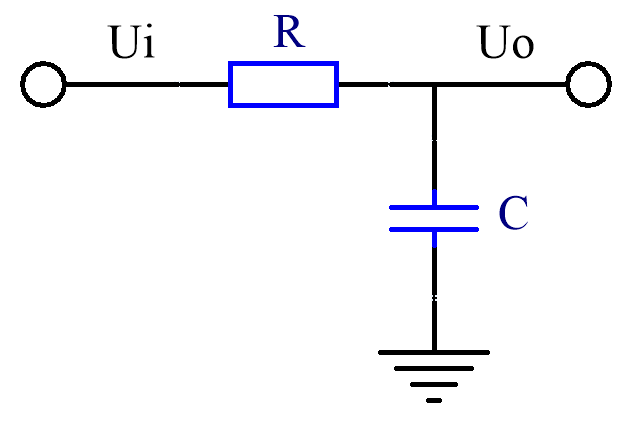 图6
图6
图6电路的幅频特性可从RC串联分压的角度理解:输出电压为RC对输入电压分压,分压比为电阻阻值和电容容抗的比值。因为频率越高容抗越低(Xc=1/(2πfC)),所以在低频处,容抗远大于电阻阻值的时候,输出电压几乎等于输入电压。在容抗等于电阻阻值的时候,电阻电压和电容电压相等,因为两个电压相位相差90°,所以电压为输入的1/√2而不是一半,也就是-3dB,该点频率为1/(2πRC),这个频率点就是极点。在高频处,容抗远小于电阻阻值的时候,大部分电压落在电阻上,电容只分得一小部分电压,所以此时的输出电压基本与电容容抗成正比。因为容抗与频率成反比,所以频率每升高多少倍,容抗变为原来多少分之一,电容电压也就变为原来多少分之一。
该电路的相频特性从电容充放电的角度理解要更直观:输入电压通过电阻给电容充电,电容电压即输出电压。当输入电压高于电容电压时,电容充电,电压上升;反之,电容放电,电压下降,如图7。在频率很低的时候,输入信号变化缓慢,有足够的时间把电容充满,所以电容电压基本上是跟随输入电压,与输入电压幅度相同,相位也相同。当频率很高的时候,输入信号变化很快,没有足够的时间给电容充电,电容在充放电过程中的电压变化相对输入信号幅度几乎可以忽略,输出电压曲线几乎贴着横坐标轴。所以在整个输入电压曲线的上半周电容电压曲线都在输入电压曲线的下方,电容处于充电状态,电容电压的峰值出现在输入电压的过零点,相位滞后输入电压90度,并且最多为90°。另外,频率越高一个周期里电容充电的时间就越短,电容电压的变化幅度就越小,输出电压就越小。在这中间的情况,电容充电过程电压也上升,电容电压与输入电压相等时达到峰值,也就是输出曲线(电容电压曲线)的峰值在它与输入电压曲线的交点处。该点与输入曲线峰值点的纵坐标之比就是输出对输入的增益;横坐标之差就是输出对输入的相移。

图7
说完极点,再说零点。幅频特性和相频特性如图8所示的频率点称为零点,可由图9电路产生。在零点处,幅度增加3dB,并在此之后每10倍频增加20dB,即频率每升高10倍幅度也变为原来的10倍。如果将幅频特性曲线折线化,则零点处斜率+1。相位上,在零点处输出信号相对输入信号超前45°,在零点的十倍频之后趋于90°,并最终停留在90°。
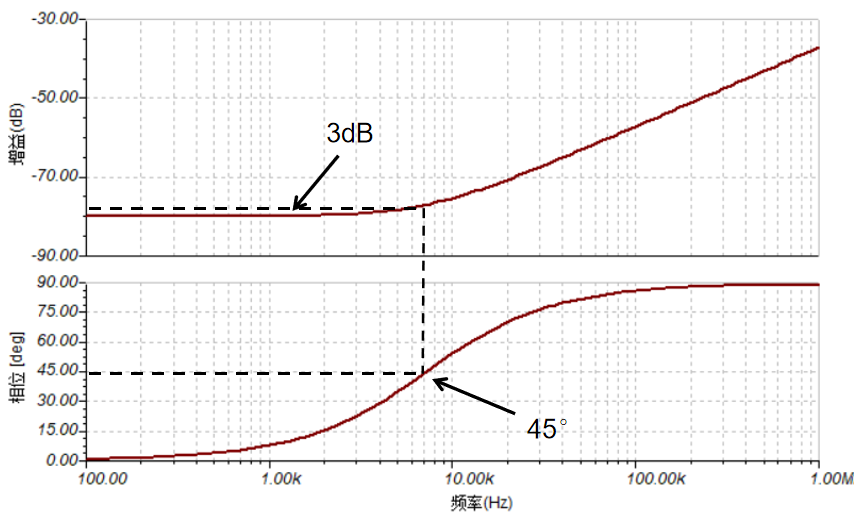
图8 零点波特图
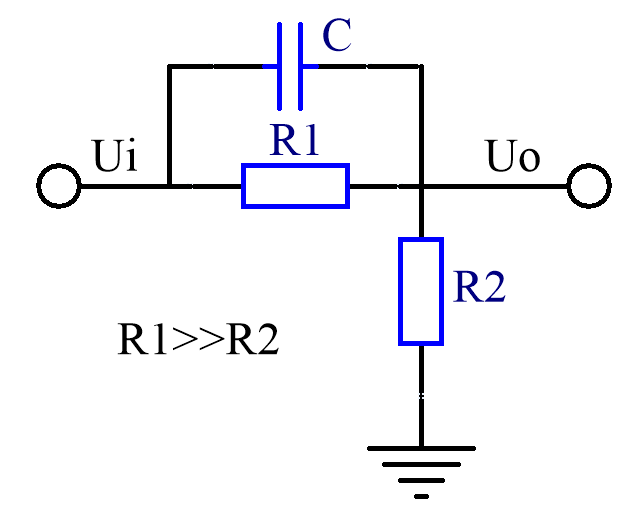
图9
图9电路中,在低频处,电容容抗远大于R1阻值,所以输出电压为输入电压经R1、R2分压。随着频率升高,容抗减小,当容抗小于R1的时候(但远大于R2),输出电压由C与R2分压,幅频特性曲线向上拐,频率升高多少倍增益也升高多少倍。容抗与R1阻值相等的频率点为零点,频率为1/(2πR1C)。另外随着频率继续升高,当容抗降低到接近R2阻值的时候,幅频特性曲线向下拐(变平),此处是一个极点。
环路中每增加一个极点将带来-90°的相移,以及幅度上每10倍频-20dB的持续衰减;每增加一个零点将带来+90°的相移和幅度上每10倍频+20dB的变化。可以通过在反馈环路中引入极点或零点,改变环路的频率响应,从而改变环路的稳定性或其他动态特性。
运放开环响应
运放最常见的开环响应是主极点响应:在低频处有一个极点,在极点之后开环增益以每10倍频-20dB的速度衰减。相位上,在极点处滞后45°,并在极点的十倍频之后趋于90°。第二个极点落在单位增益频率附近,通常在单位增益频率之后不远处。因为单位增益频率之前只有一个极点,所以相位滞后最终停留在90°,不会更多;增益上一直是每10倍频-20dB,直至穿过0dB线。这种运放在极点之后单位增益频率前任何频率处的开环增益与对应频率的乘积是一个常数,称为恒定增益带宽积运放,增益带宽积通常记为GBW或GBP。运放的开环响应为什么要设计这样后面会再次讨论。
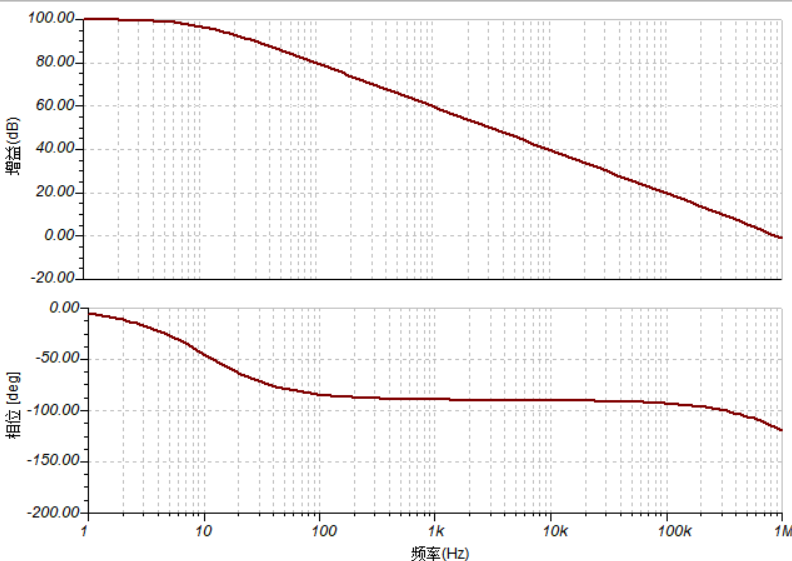
图10 运放LM358的开环响应(不同品牌会有所差异)
反馈系数
先考虑反馈电路为纯电阻的情况:因为运放的输入偏置电流很小,相对Rf和Rg上的电流可以忽略,所以反馈系数就由Rf和Rg的比值决定,即F=Uf/Uo=Rg/(Rg+Rf),并且Uf和Uo同相,反馈环节没有额外相移。如果反馈电路含电抗元件(通常为电容,这里只讨论电容),Uf同样是由Zf和Zg对Uo分压决定,区别是因为电抗跟频率有关,所以不同频率的分压比不同,并且Uf相对Uo会有相移,根据不同的连接方式,可以是滞后或者是超前,如图11(注意图中电压使用相量符号)。虽然复数阻抗形式的公式计算比较麻烦,但如果不是关注幅频曲线转折点附近的情况,可以直接用阻抗的数值进行估算,转折点附近的具体情况可以用软件仿真。当AF>>1时(即深度负反馈),闭环增益为反馈系数的倒数1/F,如果反馈电路含电抗元件,则F的大小随频率变化,也就是不同频率处放大倍数不同,此时电路就是一个有源滤波器。

图11
频率补偿
环路中每增加一个极点将带来-90°的相移,同时使增益曲线斜率-1。而当总相位滞后达到180°时,如果环路增益还没衰减到0dB以下,将会导致自激振荡。所以在环路的第二个极点十倍频后如果环路增益仍>1,就有可能自激(实际上如果没有第三个极点带来更多的相位滞后,通常是振铃,比较难自激)。
解决思路有两种:一种是在环路中引入一个频率很低的极点或者把原本的第一个极点拉到更低的频率,降低环路带宽,让第二个极点落在环路的单位增益频率后面。此时,单位增益频率之前的相移主要由第一个极点控制,如果第二极点刚好在单位增益频率处,则相位裕度为45°,如果在单位增益频率后,则相位裕度>45°,离得越远相位裕度越高,同时电路的速度也越慢。这种方式称为主极点补偿,简单说就是降低带宽使得环路相位滞后180°的频率在单位增益频率之后,是通过牺牲速度来换稳定。前面说到多数运放的开环响应为主极点响应,其内部就是引入这种类型的补偿。因为单位增益频率之前只有一个极点,所以运放在任何闭环增益下都能稳定。虽然运放内部补偿是芯片设计者的事,但这种补偿方式同样可以用在其它对速度要求不高的场合。
另一种补偿思路是在高频处引入零点,产生相位超前,以抵消极点带来的相位滞后,使得在单位增益频率处相位滞后低于180°。这里强调高频处的零点是因为引入零点除了带来相位超前外,还会使零点后增益曲线斜率+1,使单位增益移到更高的频率处。所以如果零点频率过低,就有可能使带宽拓展到原本在单位增益频率后的极点之后,电路同样不稳定。这种补偿方式后面将通过容性负载和反相输入端电容的例子进一步讨论。
引入极点使增益衰减的同时也伴随着相位滞后;引入相位超前补偿也意味着带来更高的高频增益,幅度和相位的变化总是形影相随,这里可以用波特图来直观表示。在波特图中,幅频特性曲线用对数坐标表示,相乘变为相加,相除变为相减。因为反馈系数F总是小于1,是一个分数,所以AF在波特图中可由A-1/F得到。也就是开环增益A的曲线减去1/F的曲线,两个曲线中间的那部分,它表示环路增益在不同频率处的值。如果将环路增益的幅频特性曲线折线化,不考虑转折点附近的相位变化过程,则斜率为-1对应着环路相移-90°,斜率-2对应环路相移-180°,如图12。所以在一些资料中会有以下说法:为保持环路稳定,穿越频率处斜率应为-1。说的就是环路增益衰减为1倍时相位滞后应小于180°,因为斜率-2相位滞后将达到180°。严格来说,如果不考虑第三个极点影响,在第二个极点后不远处斜率虽然为-2但相位滞后还达不到180°,仍有0°- 45°的相位余量,但这通常是不够的。通过环路增益曲线穿过横坐标轴(0dB)时的斜率可以判断电路是否稳定,如果不稳定,可以在环路中引入零点或极点,改变环路增益的曲线,使之穿过横坐标轴的斜率为-1,从而使电路稳定。

图12 A和1/F的差为环路增益(蓝色曲线)
容性负载
运放驱动容性负载可能导致自激振荡,这个输出电容有时并不是有意引入的,而是电路的寄生参数,是我们无法完全消除的东西。如图13电路,运放输出电阻Ro和负载电容CL会在反馈环路中引入一个极点(图14 fp2),频率为1/(2πRoCL),在极点处产生附加的相位滞后45°并最终趋于90°。加上运放开环特性本身的低频极点(图14 fp1)带来的90°滞后,总相位滞后将会达到180°,从而导致自激或振铃。这里要注意:上面说的输出电阻Ro指的是运放开环输出电阻,是运放本身的内阻,通常为几十欧到上千欧级别。我们平常说运放输出电阻近似为0,指的是闭环输出电阻,是深度负反馈的结果。负反馈会调节运放的输出以补偿负载电流在内阻上产生的电压,使得放大电路的输出电压几乎不随负载电流变化,所以从反馈环外看,放大电路的输出电阻就近似为0。

图13 容性负载运放电路
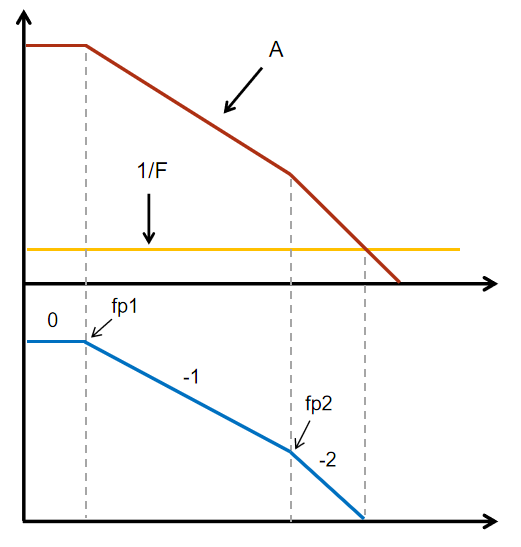
图14 容性负载电路的频率特性
回到前面,容性负载可能导致自激或振铃,所以需要对反馈环路做补偿。最简单的做法是在运放的输出和容性负载之间串一个电阻Rs(通常Rs
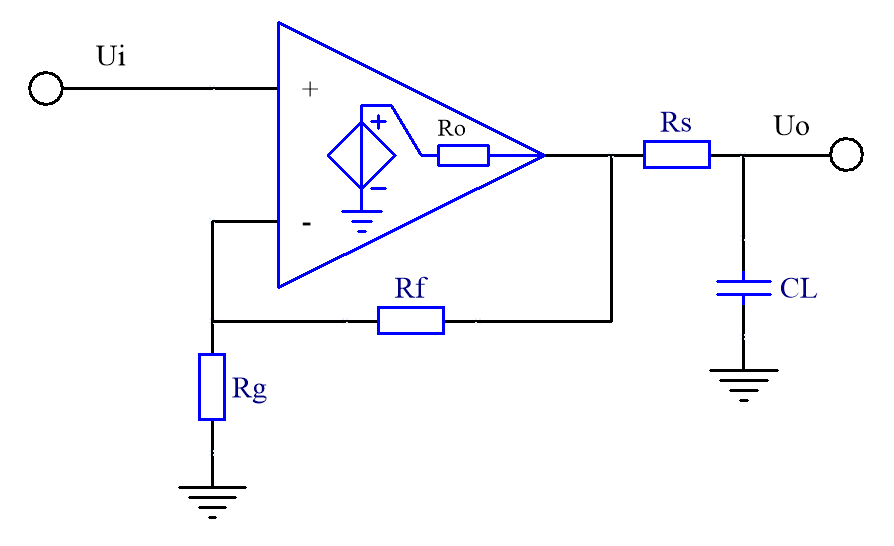
图15 加电阻Rs隔离容性负载

图16 加隔离电阻后的频率特性
改进方法是:同样用一个电阻Rs将电容和运放隔开,直流反馈取自负载端,在Rs前面再加一个电容Cf连接到反相输入端,产生相位超前的补偿(如图17),这种方式也称为环内补偿。因为直流反馈取自负载端,所以负载端的电压不受输出电流影响。此外,还可以在输出端加RC减振电路来抑制自激或振铃(如图18),这种做法常用于音频功放电路。原理有点类似于主极点补偿的做法,都是通过降低环路带宽来消除自激:在输出端加一个足够大的电容,其容量远大于原本的负载电容,降低环路带宽。然后在大电容上串联一个电阻(阻值小于Ro),引入一个零点来抵消大电容新产生的低频极点。

图17 环内补偿
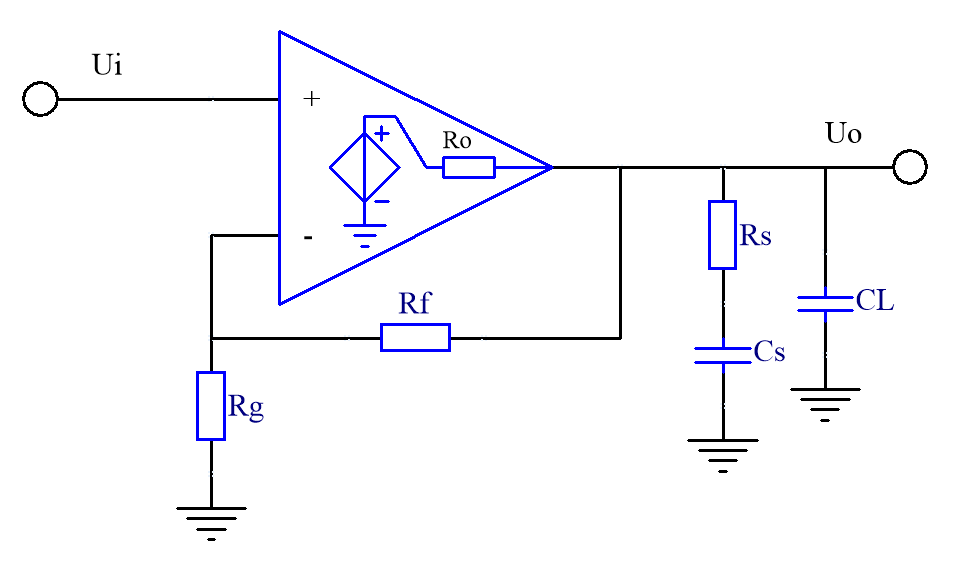
图18 加RC减振电路
反相输入端电容
有时候,反相输入端的对地电容Cn也可能导致自激或振铃,比如反馈电阻取值过大或者运放带宽很高的时候。如图19电路,反相输入端对地电容在反馈回路中的形式与容性负载一样,都是一个RC低通环节,同样会产生一个极点(图20 fp2),导致相位滞后,fp2=1/(2π(Rg//Rf)Cn)。虽然该电容容量很小,通常为几pF到十几pF级别,但如果反馈电阻取值过大,产生的极点频率就会比较低,使得在较低的频率处相位滞后就达到180°。如果运放的带宽又比较高,在该频率处环路增益仍大于1,就会导致自激。比如运放GBW=20MHz,Cn=10pF,Rg=100k,Rf=400k,则产生的极点为1/(2π(Rg//Rf)Cn)=199kHz。在十倍极点频率处,也就是频率2MHz处,相位滞后将接近90°(严格说是84°),加上运放开环响应的低频极点产生的90度,总相位滞后将接近180。该频率处开环增益A=10,反馈系数F=1/5,环路增益AF=2,满足自激振荡的条件。当然,上面说的情况比较极端,实际上如果没有第三个极点产生更多的相位滞后,更多的是表现为振铃,但不管哪一种情况都是不希望出现的。

图19 含反相输入端电容的电路
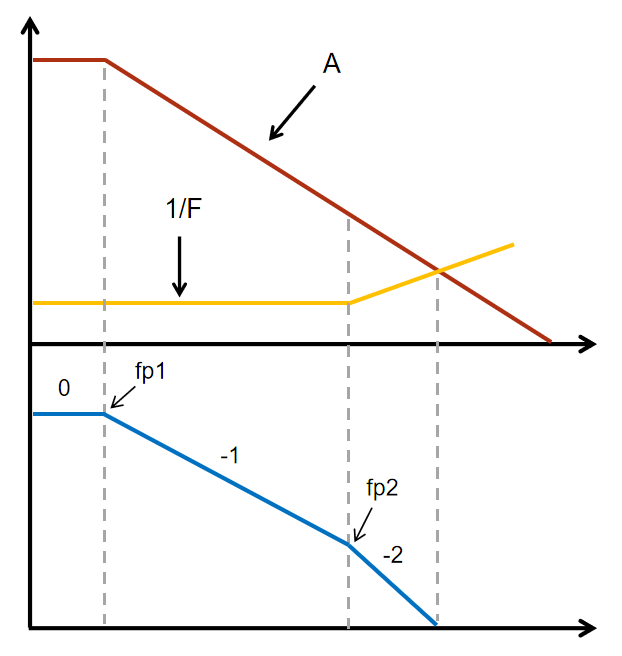
图20 图19电路的频率特性
最简单的解决方法当然就是在保持Rf和Rg比值不变的情况减小它们的阻值,使极点落在更高的频率处。如果不想减小阻值,也可以给反馈电阻Rf并上一个电容Cf(如图21),引入一个零点,产生相位超前,来抵消极点的影响。Cf取多大呢?容量大了会降低闭环带宽;容量小了相位裕度不够。通常取Cf=(Rg/Rf)·Cn,让产生的零点刚好与极点完全相抵消。Cf的取值是这么来的:反馈电压是Rg和Rf对输出的分压,如果取Xcn/Xcf = Rg/Rf,让Cn和Cf的分压比和Rg、Rf一样,则反馈系数与频率无关,Cn的影响被抵消,此时Cf/Cn = Rg/Rf,即Cf=(Rg/Rf)·Cn。使用示波器探头10X档时调节探头侧面螺丝对探头进行补偿就是这个原理,通过改变电容Cf,使探头的传输特性平坦。不过,有时候我们并不知道Cn具体多大,也就不知道怎么计算Cf。我们可以从一个比较小的容量开始,慢慢加大,测输出的阶跃响应,直到过冲在可接受的程度。

图21 加反馈电容Cf补偿
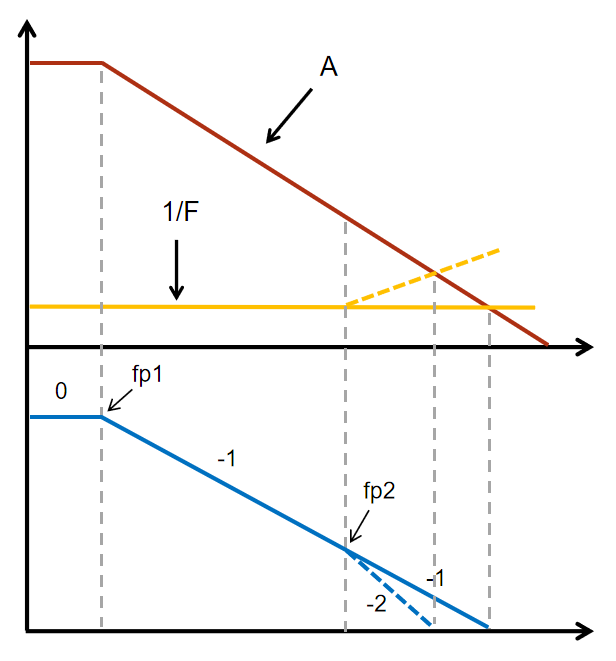
图22 加Cf后的频率特性
一个例子
这里有一个例子可以用来说明环路稳定性的问题:TL431电压基准电路的负载电容大小和稳定性的关系。如图23所示,从TL431数据手册可以看到:当负载电容容量很小或很大时都不会自激,容量不大不小时则容易导致自激振荡。比如2.5V输出时(A曲线),容量小于6nF或者大于3uF都是稳定的,在这之间则不稳定。同时可以看到,输出电压越高,则不稳定范围越小。原因就是当负载电容容量很小时,电路内阻和负载电容产生的极点频率比较高,没法在环路单位增益频率内产生足够大的相位滞后,所以电路是稳定的。当负载电容容量很大时,电路内阻和负载电容产生的极点频率很低,降低了环路带宽,在第二个极点使环路相移达到180°前增益已衰减到0dB以下,所以电路同样是稳定的。另外,输出电压越高,R1与R2的比值越大,反馈系数越小,环路增益越小,所以导致不稳定的容量范围就越小。

图23 TL431数据手册截图
写在最后
总结说,当反馈环路的总相位滞后达到180°时,如果环路增益仍大于1,就会导致自激振荡。抑制自激振荡主要有两个思路:可以是降低环路带宽,使得环路总相位滞后达到180°时环路增益小于1;或者是引入相位超前补偿,使得环路增益降低到1倍时相位滞后小于180°。
上面讨论的自激振荡的原因和判断方法,以及频率补偿的思路,同样也适用于其它形式的反馈电路,比如LDO和DCDC等。有时候,运放也可以作为大的反馈环路的一环,比如放大电流采样电阻上的电压,将输出接到DCDC的电压反馈引脚,构成恒流电路。这时候影响大环路稳定性的是运放的闭环特性,而影响小环路稳定性的是它本身的环路特性。通过改变运放闭环特性对大环路做频率补偿的同时,要注意这种改变对小环路稳定性的影响,因为某些补偿方式对大环路来说是朝着稳定的方向改变而对小环路来说却是朝着不稳定的方向。
-
全差分运放CMFB负反馈环路稳定性分析2023-07-14 4225
-
运放的基本原理和稳定性分析2023-07-24 4548
-
TINA可以进行运放的稳定性分析吗?2024-09-04 287
-
【运放稳定性分析】TI 高精度实验室 运放培训笔记2016-04-03 4761
-
开关电源增益稳定性分析2018-10-22 2134
-
开关电源环路稳定性分析2020-05-31 3933
-
开关电源环路稳定性分析(二)2022-11-22 6724
-
《运放电路环路稳定性设计 原理分析、仿真计算、样机测试》+理论与实际结合加深理解和实战运用2023-05-22 1549
-
典型二阶系统设计及其瞬态响应和稳定性分析2008-10-16 14903
-
频率响应法-相对稳定性分析2009-07-27 3452
-
运放稳定性分析2016-02-19 975
-
运放稳定性分析详解(五)2016-08-08 911
-
线性定常系统的瞬态响应和稳定性分析2016-09-01 1862
-
电源稳定性分析-Moku:Lab频率响应分析仪应用指南2022-03-17 1771
-
运放系统稳定性原理 运放的频率补偿2023-10-25 1800
全部0条评论

快来发表一下你的评论吧 !

