如何控制使用长输出线时的传导EMI（中）

如何控制使用长输出线时的传导 EMI（中）

简介

本文为分析并改善长线负载下过高传导EMI问题系列文章之中篇。上篇回顾了共模 (CM) EMI 模型，并考虑了电场耦合和磁场耦合的影响；中篇将利用一系列公式来探讨传输线对输出长线对地阻抗的影响；下篇将总结三种 EMI 降噪方法，同时分析和预测谐振峰值。

输出长线对地阻抗

如果输出线较长，在传导的高频频段，我们需要考虑它的传输线效应。电力电子工程师朋友们在日常工作中可能很少会用到这部分的内容，因此首先介绍一下相关的概念。

当电路尺寸与要考察的频率对应的波长相近时，电路的相关参数，如电压、电流、阻抗等，会由集中参数变为分布参数。

对于传输线的每一小段，如图 1所示，我们可以考察它的单位电感、电阻、电容以及电导。

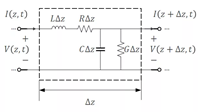
图1: 传输线模型

传输线上的电流和电压分布可以用公式（1）来计算：

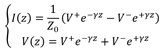
其中Z0为传输线的特征阻抗，γ为传输常数。当传输线上的损耗（如图1中的R和G）可以忽略不计时，Z0可以用公式（2）来估算：

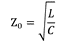
而γ可以用公式（3）来计算：

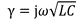
图2显示出输出线所具有的几何形状，这意味着我们可以利用电磁场理论来求得参数。

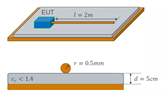
图 2：输出线对地的几何模型

如若忽略损耗，则可以使用公式 (4) 估算电容：

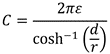
其中d代表传输线与参考地之间的距离，r为传输线的半径，ε为介质的介电常数。系统电感可以用公式 (5) 计算：

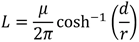
其中µ为介质的磁导率。这里因为是共模噪声，所以输出的两条线近似合并为同一导体考虑。

由于我们的输出线的末端与参考地之间没有连接，可以认为是近似开路（末端电流为0），我们可以将（2）-（5）代入到（1），得到最终输出线上的电流与电压表达式。因此，可以得到，对于长度为l的输出线，它的阻抗(ZOC)可以用（6）表示：

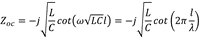
其中ω为角频率(2πf)；而λ即为波长(1 / (f x (√LC))。

通过（6），根据三角函数的性质，在l为四分之一波长的奇数倍时（如1/4λ，3/4λ等），这个阻抗将发生串联谐振，导致EMI传播路径上的阻抗大幅减小，因此，我们会发现有EMI峰的存在。如果传输线长为2m，那么根据我们的实际情况，1/4λ，3/4λ对应的频率分别在31.6MHz和95.1MHz，这也就解释了为什么上篇图3的频谱上会出现这两个峰。

这个理论也很容易直接通过测量进行验证。图3为不同长度传输线的对地阻抗测量结果，显然，对于2m的输出线，其阻抗谢振峰的位置符合我们之前的计算结果，这也解释了EMI测量结果中的谐振峰。另外，输出线越短，谐振发生的频率也越高。

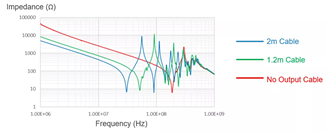
图 3：不同长度的传输线接地阻抗测量结果

最后，对应1/4λ的频率可以使用公式 (7) 进行估计：

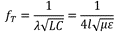
通过上式可以确认，输出线与参考地之间的距离以及线径不会影响谐振的位置，谐振只与输出线的长度有关。

结论

在本文中，通过计算电流和电压的分布、传输线损耗、电感、电容、最终输出线阻抗和频率，我们得到了上篇中描述的CM EMI模型。在下篇中，我们将分析多种降噪方法的效果，并最终实现长线负载的成功输出。

审核编辑：汤梓红