为什么GBDT用回归树不用分类树？CART决策树是怎么计算基尼值呢？

一、背景

集成学习Boosting一族将多个弱学习器(或称基学习器)提升为强学习器，像AdaBoost, GBDT等都属于“加性模型”(Additive Model)，即基学习器的线性组合。1997年Freund和Schapire提出的AdaBoost，它是先从初始训练集训练出一个基学习器，然后基于基学习器的在这一轮的表现，在下一轮训练中给预测错的训练样本更大权重值，以达到逐步减少在训练集的预测错误率。这种训练机制像不像做一套卷子，有些重难点题做不出来，那下次又给你做同样的卷子，但不同的是：之前你做错的重难点题占有很大的分值比重，这样你会将更多重心放在了这些难题上，从而提高你的学习表现。那除了这种方式，还有没有其他方法攻克考题上的重难点？有，就是死磕到底，找到这题错在哪？基于此错误继续去做这道题，直到做对为止。这跟GBDT [1] 的工作机制就很像了，它是先产生一个弱学习器(CART回归树模型)，训练后得到输入样本的残差，然后再产生一个弱学习器，基于上一轮残差进行训练。不断迭代，最后加权结合所有弱学习器得到强学习器。GBDT的一个应用示意图如下（某样本预测值 = 它在不同弱学习器所在叶子节点输出值的累加值）：

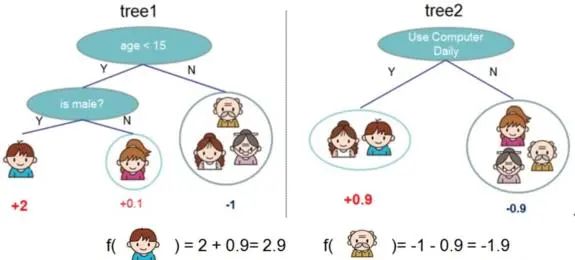
图1：GBDT应用示意图

二、GBDT

第二部分目录如下：

1.背景知识

• GBDT弱学习器
• GBDT模型框架

2.GBDT回归

3.GBDT分类

• GBDT二分类
• GBDT多分类

1. 背景知识

GBDT可用于回归和分类任务。在深入了解它在回归或分类任务上的训练细节之前，我们先了解一些相关的背景知识。

（1）GBDT弱学习器

决策树是IF-THEN结构，它学习的关键在于如何选择最优划分属性。西瓜书 [2] 提到：“随着划分过程不断进行，我们希望决策树的分支结点所包含的样本尽可能属于同一类别，即结点的“纯度”(Purity)越来越高”。衡量纯度的指标有多种，因此对应有不同类型的决策树算法，例如ID3决策树 (以信息增益Information Gain作为属性划分标准)，C4.5决策树 (以增益率Gain Ratio选择最优划分属性)，CART决策树 (使用基尼指数Gini Index)来选择划分属性。

决策树那么多种，为什么GBDT的弱学习器就限定使用CART决策树？

A： 原因如下所示 (具体细节不展开)：

• ID3决策树只支持类别型变量，而C4.5和CART支持连续型和类别型变量。
• C4.5适用于小样本，CART适用于大样本。

CART决策树是怎么计算基尼值呢？

A： 假设当前数据集D中第k类样本所占比例为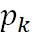 (k=1,2,…,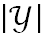)，则基尼值为：

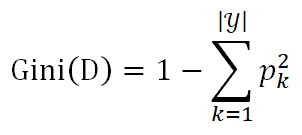
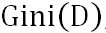反映了从数据集D随机抽取两个样本，其类别标记不一致的概念，因此越小，数据集D的纯度越高。基于此，属性a的基尼指数定义为：

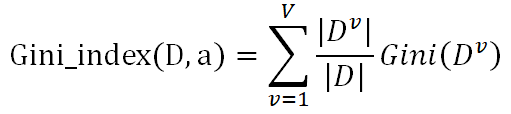
假设属性a有V个可能的取值{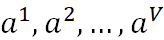}，则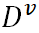是指第v个分支结点包含D中所有在属性a上取值为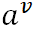的样本。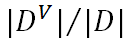是给分支结点赋予权重，获得样本数更多的结点，影响更大。

举个具体计算基尼指数的例子，假如按照“芯片为高通骁龙865和非高通骁龙865进行机型档位划分”：

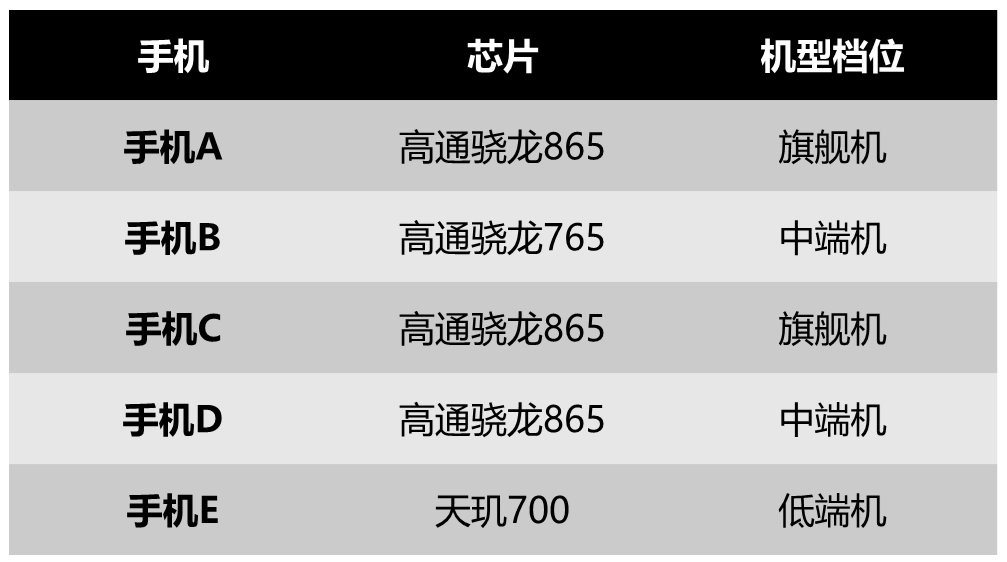
表1：基尼指数计算样例集

当芯片为高通骁龙865时，有旗舰机2个，中端机1个：

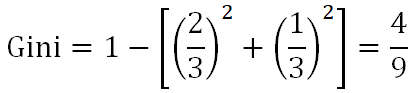
当芯片非高通骁龙865时，有中端机1个，低端机1个：

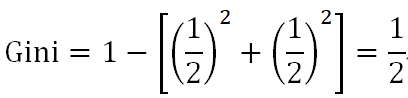
最后，特征”芯片”下数据集的基尼指数是：

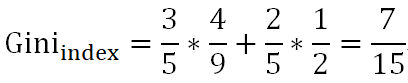
为什么GBDT用回归树，不用分类树？

A： 因为GBDT要计算残差，且预测结果是通过累加所有树结果得到的。因此分类树没法产生连续型结果满足GBDT的需求。

（2）GBDT模型框架

图2：GBDT算法实现流程图及伪代码 [3]

GBDT的伪代码如图2所示，假设我们有个样本集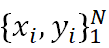，想用M个弱学习器加性组合成GBDT强学习器，我们得按以下步骤进行实现 (详情参考 [4])：

1）初始化一个弱学习器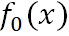。它使损失函数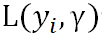最小化，具体如下：

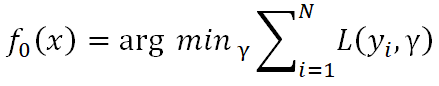
这里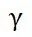是什么呢？请接着看下去，假设这里损失函数为平方损失，则对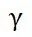求导：

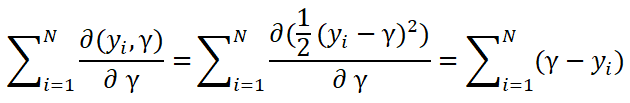
由于这里的损失函数为凸函数，所以只要令上面这个导数为0即可，那么可以求得：

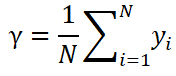
因此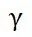，是所有训练样本标签值的均值，它是一个常数，所以弱学习器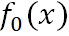就只有一个根节点。

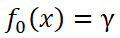
注意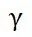：因损失函数不同而不同。

2）迭代训练m = 1, 2, … , M棵树。

（a）对每个样本i = 1, 2, …, N，计算负梯度:

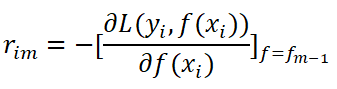
（b）将上步（a）得到的负梯度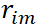作为新样本值，将新数据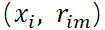, I = 1, 2, …, N作为下颗树的训练数据，拟合得到新树，新树上的叶子节点区域为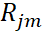（j = 1, 2, …,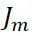，其中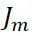为叶子结点的个数）。

（c）对每个叶子节点j = 1, 2, …,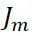 ，计算最佳拟合（即使损失函数最小，拟合叶子节点最好的输出值）：

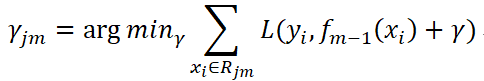
（d）更新强学习器：

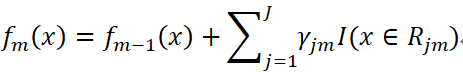
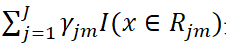是CART回归树模型的表达式，其中J是指数据集被划分为J个单元（即叶子节点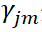），是第m轮迭代训练下，CART树第j个单元的输出值。而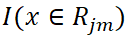是指示函数，若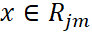，则I=1，否则I=0。这里第m轮下的强学习器 = 第m-1轮下的强学习器 + 第m轮的弱学习器。

3）输出最终学习器GBDT:

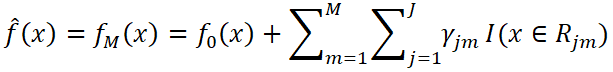
上述公式展示的就是一系列弱学习器累加后得到强学习器的结果。

负梯度和残差的关系是什么？

A： 负梯度是函数下降最快的方向，也是GBDT目标函数下降最快的方向，所以，我们用负梯度去拟合模型。而残差只是一个负梯度的特例，当损失函数为均方损失时，负梯度刚好是残差（这点在上面 "对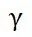求导" 处有做假设展示）。

2. GBDT回归

上面”GBDT通用框架”就是以平方损失为损失函数的一种GBDT回归模型学习过程，不同损失函数导致使用的负梯度不同，因此也就产生了不同的GBDT回归算法，总结了下GBDT回归模型所用的损失和负梯度如下：

表2：GBDT回归树常用损失函数及负梯度 [5]

这里特别说下Huber损失，它对于中间附近的点 (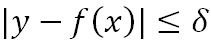)采用均方误差，对远离中心的异常点 (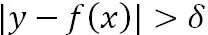)，采用绝对损失。边界点δ的值受绝对损失函数而不是平方误差损失控制，定义了这些被认为是“离群点”的残差值。总的来说，Huber结合了均方差和绝对损失，在抵抗长尾误差分布和异常值的同时，还保持了对正态分布误差的高效率。它和分位数损失一样，适用于稳健回归，用于减少异常点对损失函数的影响。

3. GBDT分类

由于分类有二分类和多分类任务，所以GBDT分类有所区别，这里分开对它们进行展开解释：

** （1） GBDT二分类**

我们上面也讲到了，GBDT本质上就是一系列弱学习器之和：

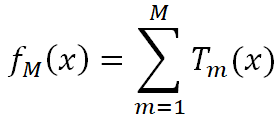
而GBDT分类跟逻辑回归的思路是类似的，将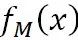的作为下列函数的输入，便可以得到类别概率值：

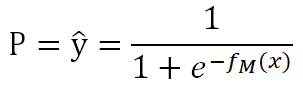
假设样本独立且同分布，极大似然估计(即选取合适的参数使被选取的样本在总体中出现的可能性最大)的损失函数为：

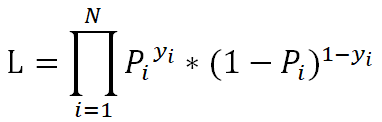
为了方便对损失函数求导，会加入对数，求最大对数似然估计：

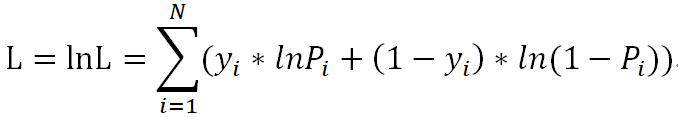
上面的损失函数并非最终的函数，而是最大似然估计函数（数值越大越好），由于损失函数应该使越小越好，所以要对上面的L取相反数，同时为了得到平均到每个样本的损失值，要除以样本数N，这样得到了最终的损失函数：

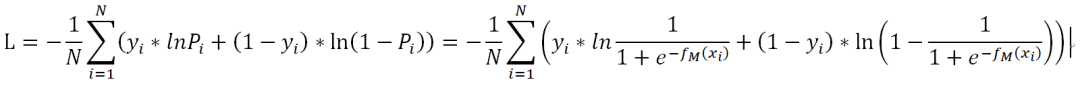
对损失函数计算负梯度：

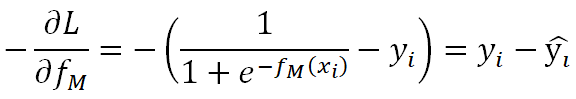
由此看来，GBDT负梯度即为残差，表示真实概率和预测概率的差值。接下来计算过程跟着GBDT通用框架进行就好了。

** （2） GBDT多分类**

GBDT多分类原理跟Softmax一样的，假设我们有k个类别，将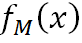作为以下函数的输入，便可以类别q对应的概率值：

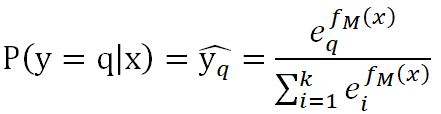
其损失函数为：

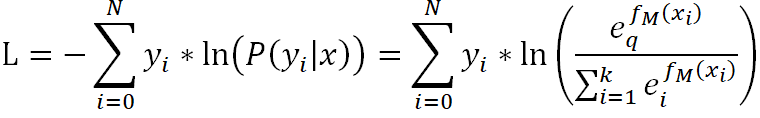
多类别任务下，只有一个类别是1，其余为0，假设这不为0的一类为q，我们对它Softmax的损失函数求负梯度得：

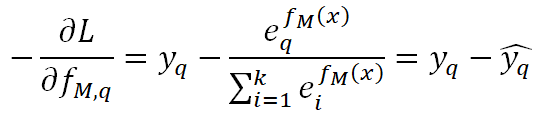
跟二分类一样，本质上负梯度就是真实概率和预测概率的插值。

三、其它

第三部分讲下GBDT的其它内容：

1. 正则化

2. 优缺点

3. 与RF的对比

1. 正则化

GBDT采用了三种正则化手段：

（1）学习率v和树数量M的平衡

我们前面得到，第m轮下的强学习器 = 第m-1轮下的强学习器 + 第m轮的弱学习器，如下：

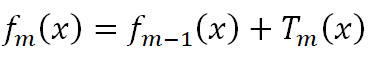
GBDT原论文提到，树数量越多，越容易过拟合，所以限制树数量可以避免过拟合，但历史研究又给出：通过收缩 (即学习率v减少) 实现的正则化比通过限制项 (即树数量M减少) 实现的正则化效果更好。这是什么意思呢？请先看下面的公式：

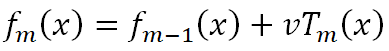
该公式加入了学习率v，这里跟神经网络的学习率相反，如果我们学习率下降，每个树的贡献就会减低，反而还实现了正则化，但如果我们放开训练(即不固定树数量)，只减低学习率的话，GBDT还是会过拟合，因为产生了更多的树。因此，GBDT作者建议，我们要实现v-M之间的权衡，理想的应该是在正则效果合适下，学习率降低的同时，也能尽可能保证树数量少些。这里当然也有出于对计算资源的考虑，增加M会带来计算开销。

（2）子采样比例

子采样是将原数据集中抽样一定的样本去拟合GBDT。与随机森林不同的是，GBDT采样不放回抽样，因为GBDT串行训练要求所有弱学习器使用同一套样本集，不然在不同抽样样本空间计算的残差，缺乏一致性。

（3）决策树常用正则化手段

这块的参数都涉及到弱学习器树本身的正则化，例如：决策树最大深度、划分所需最少样本数、叶子节点最少样本数、叶子节点最小样本权重、最大叶子节点数、节点划分最小不纯度等。

2. 优缺点

优点：

• 采用基于“残差”(严格来说是负梯度)的Boosting集成手段。
• 适用于回归、二分类和多分类任务。
• 预测精度比RF高。
• 对异常值的鲁棒性强（采用了Huber损失和分位数损失）。

缺点：

• 串行方式的模型训练，难并行，造成计算开销。
• 不适合高维稀疏离散特征。这是决策树的痛点，比如动物类别采用one-hot编码后，会产生是否为狗，是否为猫一系列特征，而若这一系列特征中大量样本为狗，其它动物很少，那么树在划分属性时，很容易就划分为“是否为狗”，从而产生过拟合，它不像LR等线性模型f(w,x)的正则化权重是对样本惩罚（可以实现对狗样本给与更大的惩罚项），而树的惩罚项往往是树结构相关的，因此样本层面的惩罚较小，使得在高维稀疏特征时，GBDT表现不好。

3. 与RF的对比

[4] 总结的很好，我就不重复造轮子了：

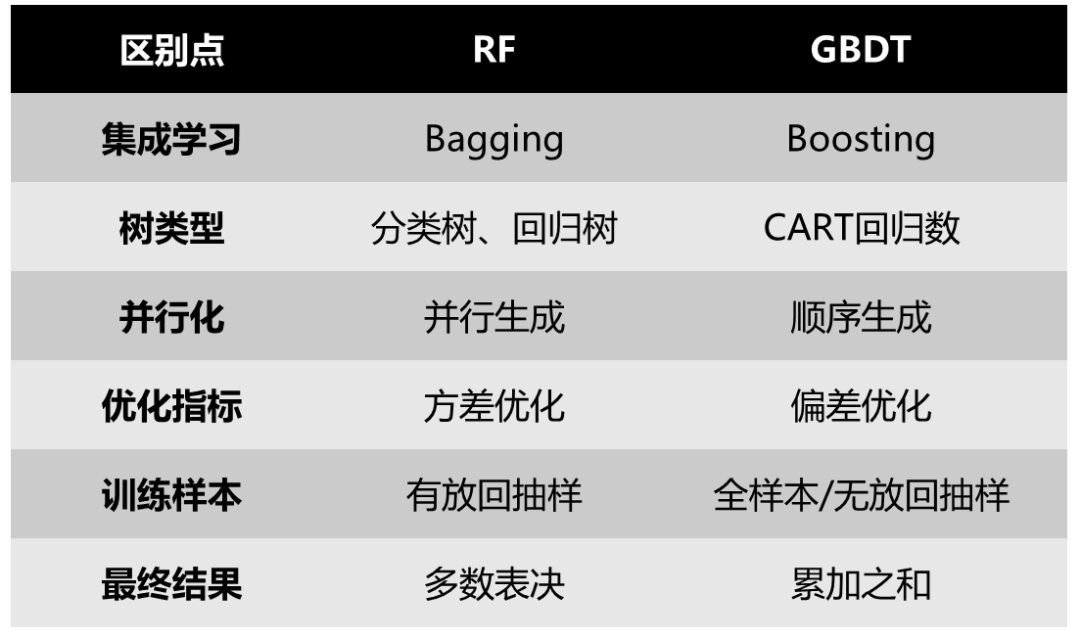
图3：GBDT与RF的区别 [4]

四、代码参考

scikit-learn已提供封装好的库直接调用就好了，受限于篇幅，这里不详细展开，详见官方文档 [6]。

from sklearn.datasets import make_regression
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.model_selection import train_test_split


X, y = make_regression(random_state=0)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
reg = GradientBoostingRegressor(random_state=0)
reg.fit(X_train, y_train)
reg.predict(X_test[1:2])
reg.score(X_test, y_test)