自动驾驶 RRT算法原理解析

1 RRT算法的简介

天下武功唯快不破，快是 RRT 的最大优势。RRT 的思想是快速扩张一群像树一样的路径以探索空间的大部分区域，找到可行的路径。

RRT 算法是一种对状态空间随机采样的算法，通过对采样点进行碰撞检测，避免了对空间的精确建模带来的大计算量，能够有效地解决高维空间和复杂约束的路径规划问题。

与PRM类似，该方法是概率完备且非最优的。可以轻松处理障碍物和差分约束（非完整和动力学）的问题，并被广泛应用于机器人路径规划。

2 RRT算法原理

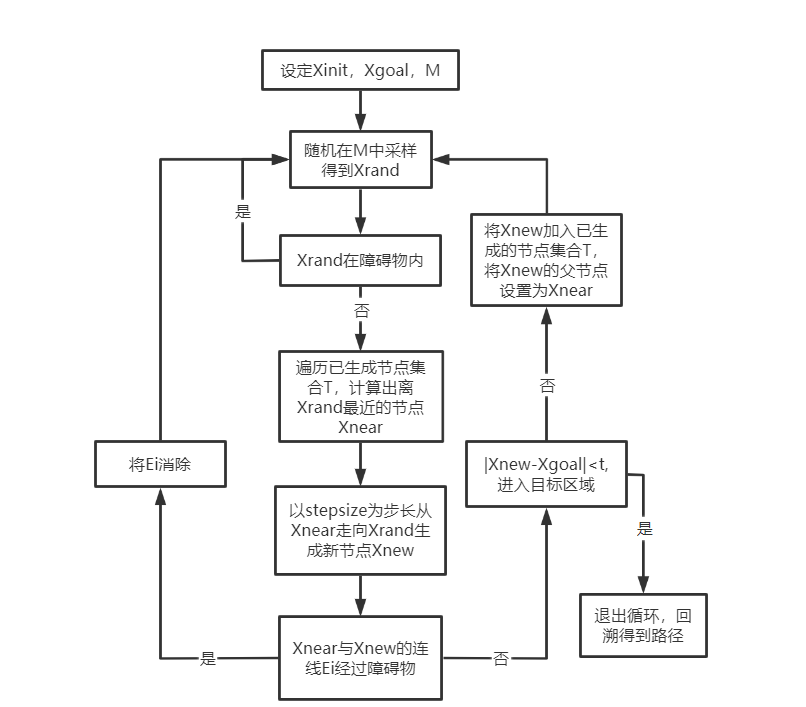
2.1 算法流程

（1）设定初始点  与目标点 ，自行设定状态采样空间 

（2）进行随机采样得到采样点 ，如果采样点  在障碍物内，则重新随机采样

（3）若不在障碍物内，计算该采样点  与集合  (已经生成的节点) 中的所有节点之间的距离，得到离得最近的节点 ，再从节点  以步长  走向节点  ，生成一个新的节点 ，若  与  的连线  经过障碍物，则重新随机采样

（4）经过反复迭代，生成一个随机扩展树，当随机扩展树中的子节点进入了我们规定的目标区域，便可以在随机扩展树中找到一条由从初始点到目标点的路径。

2.2 算法伪代码

可以将伪代码与上述算法流程对照起来看

2.3 算法流程图

3 RRT算法matlab实现

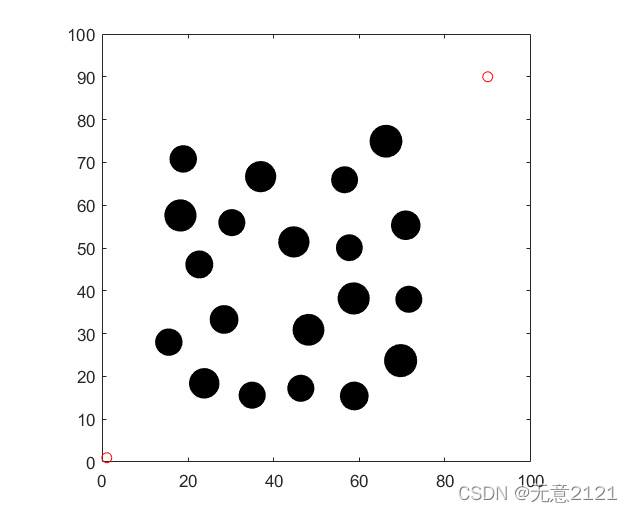
3.1 测试地图

%随机生成障碍物
function [f,n1]=ob(n)
f=[];%储存障碍物信息
n1=n;%返回障碍物个数
p=0;
for i=1:n
    k=1;
    while(k)
        D=[rand(1,2)*60+15,rand(1,1)*1+3];%随机生成障碍物的坐标与半径，自行调整
        if(distance(D(1),D(2),90,90)>(D(3)+5)) %与目标点距离一定长度，防止过多阻碍机器人到达目标点
            k=0;
        end
        for t=1:p  %障碍物之间的距离不能过窄，可自行调整去测试
            if(distance(D(1),D(2),f(3*t-2),f(3*t-1))<=(D(3)+f(3*t)+5))
                k=1;
            end
        end
    end
    %画出障碍物
    aplha=0:pi/40:2*pi;
    r=D(3);
    x=D(1)+r*cos(aplha);
    y=D(2)+r*sin(aplha);
    fill(x,y,'k');
    axis equal;
    hold on;
    xlim([0,100]);ylim([0,100]);
    f=[f,D];
    p=p+1;%目前生成的障碍物个数
end
hold all;

3.2 distance函数

function f=distance(x,y,x1,y1)
   f=sqrt((x-x1)^2+(y-y1)^2);

3.3 RRT算法

clc
clear all
[f,n1]=ob(10);%随机生成障碍物
Xinit=[1,1];%定义初始点
Xgoal=[90,90];%定义目标点
plot(Xinit(1),Xinit(2),'ro');
plot(Xgoal(1),Xgoal(2),'ko');
T=[Xinit(1),Xinit(2)];%已生成节点集合用顺序表的数据结构存储
Xnew=Xinit;
D(1)=0;%初始节点的父节点指向0
while distance(Xnew(1),Xnew(2),Xgoal(1),Xgoal(2))>3  %进入目标区域
    Xrand=round(rand(1,2)*100)+1;%状态采样空间：横纵坐标均为整数，范围1~100
    k=1;%进入循环
    while k==1
        k=0;%初始化采样成功
        for i=1:n1
            if distance(Xrand(1),Xrand(2),f(i*3-2),f(i*3-1))<(f(i*3)+1)%判断随机采样点是否在障碍物内
                k=1;%采样不成功
                break;
            end
        end
        Xrand=round(rand(1,2)*100);%重新采样
    end
    min=10000;
    for i=1:size(T,2)/2 %遍历已生成节点集合
        if distance(T(2*i-1),T(2*i),Xrand(1),Xrand(2))Xnew(1)
        caiyang=-0.001;
    else
        caiyang=0.001;
    end
    for i=Xnear(1)Xnew(1)%均匀采样进行碰撞检测
        for j=1:n1
            if distance(f(3*j-2),f(3*j-1),i,Xnear(2)+(i-Xnear(1))/(Xnew(1)-Xnear(1))*(Xnew(2)-Xnear(2)))<=(f(3*j)+1)
                t=1;%代表碰撞
                break;
            end
        end
        if t==1
            break;
        end
    end
    if t==0
        T=[T,Xnew(1),Xnew(2)];
        for i=1:size(T,2)/2 %遍历已生成节点集合
            if (T(i*2-1)==Xnear(1))&&(T(i*2)==Xnear(2))  %得到最近的节点的索引
                D(size(T,2)/2)=i;%记录父节点
                break;
            end
        end
        plot([Xnew(1),Xnear(1)],[Xnew(2),Xnear(2)],'b-');hold on;pause(0.005);
        plot(Xnew(1),Xnew(2),'r.');xlim([0,100]);ylim([0,100]);
    end
end
i=size(T,2)/2;
jg=[i];
while D(i)
    i=D(i); %通过链表回溯
    if D(i)~=0
        jg=[D(i),jg];%存储最短路径通过的节点
    end
end
Fx=T(jg(1)*2-1);Fy=T(jg(1)*2);
i=2;
while jg(i)~=size(T,2)/2
    x=T(jg(i)*2-1);
    y=T(jg(i)*2);
    plot([x,Fx],[y,Fy],'g-');hold on;pause(0.05);
    Fx=x;Fy=y;
    i=i+1;
end
 plot([T(jg(i)*2-1),Fx],[T(jg(i)*2),Fy],'g-');hold on;pause(0.05);

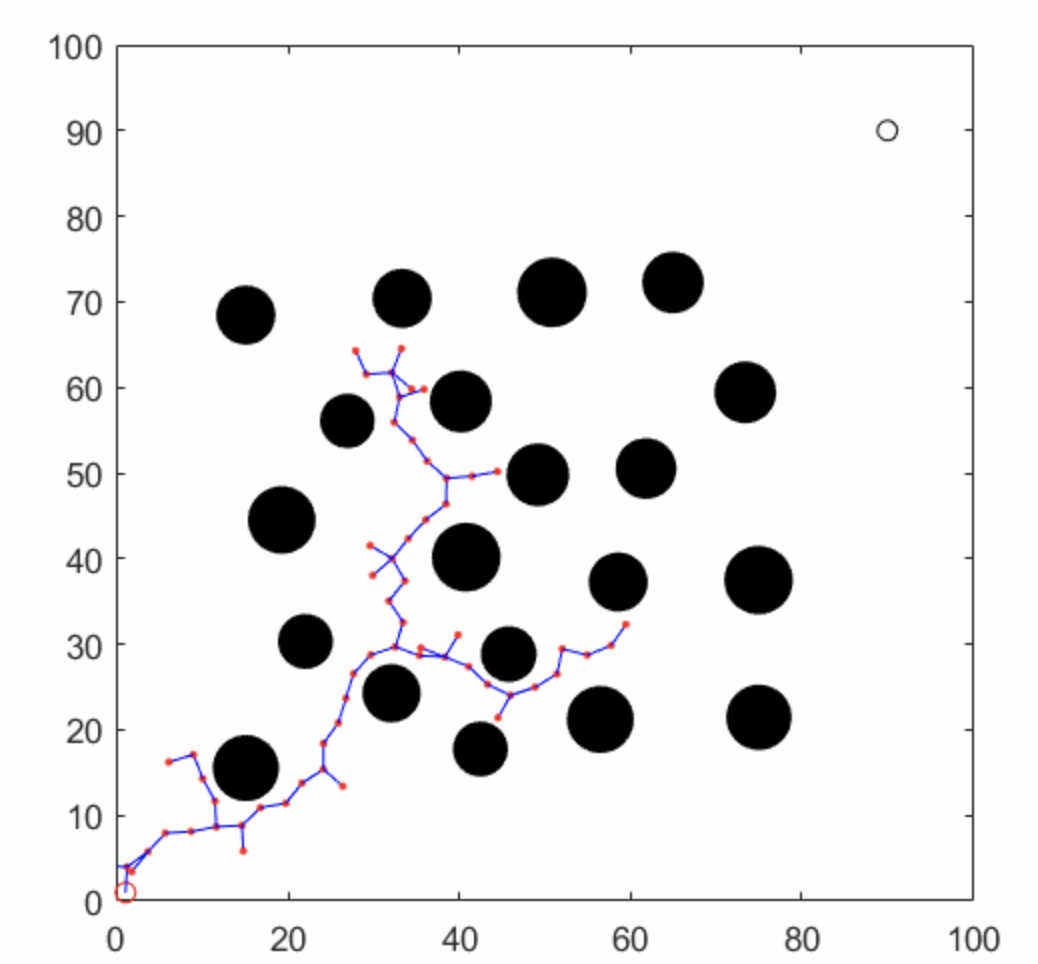
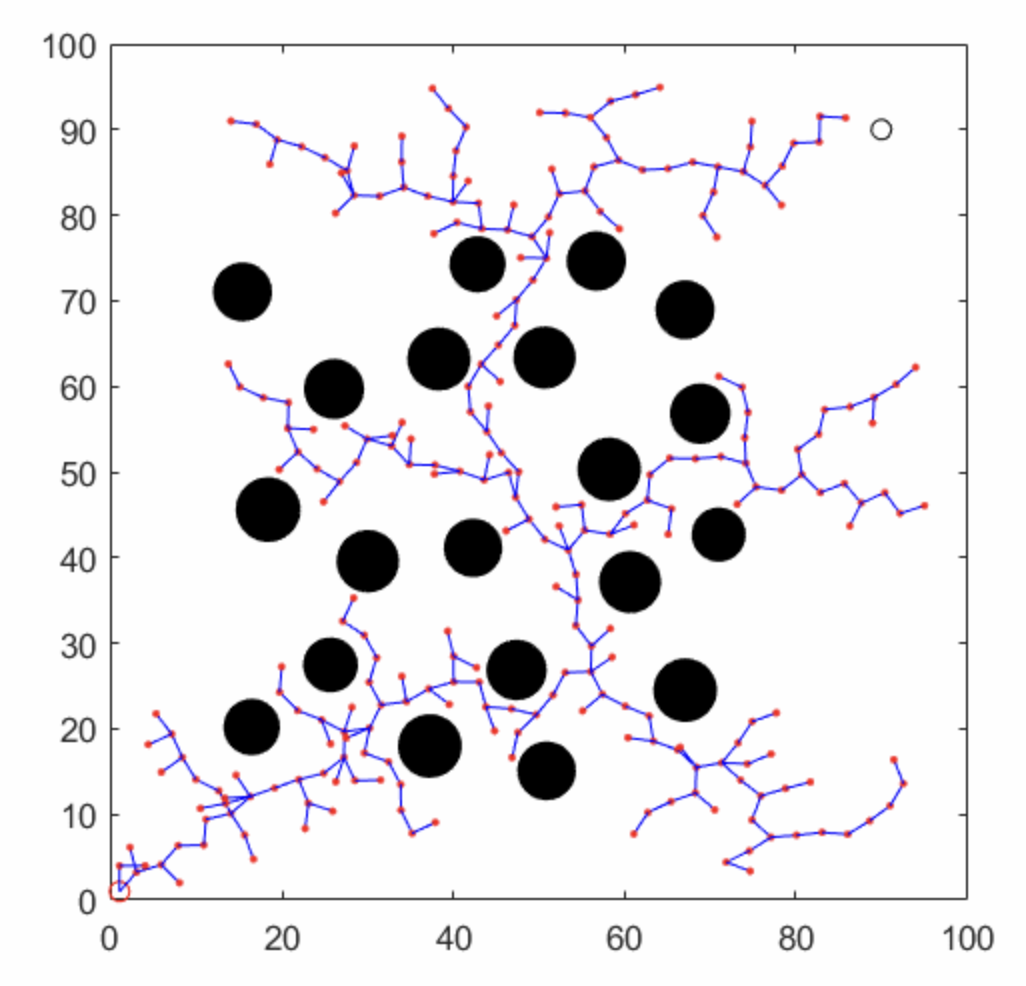
3.4 动画效果

4 RRT的缺陷

（1）很明显RRT算法得到的路径不是最优的

（2）RRT算法未考虑运动学模型

（3）RRT算法对于狭小的通道的探索性能不好，如下图的对比，有可能探索不到出口

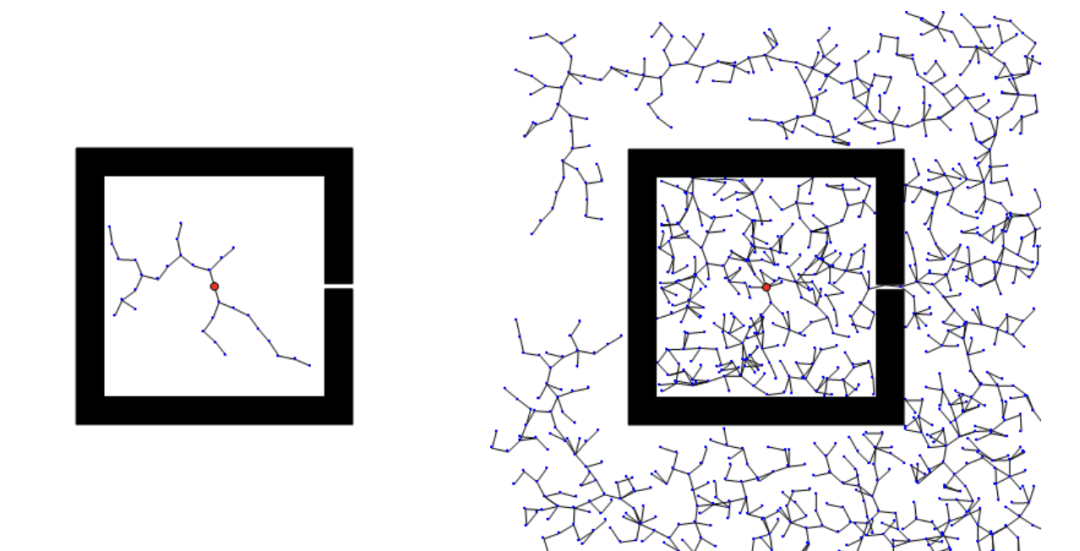
（4）没有启发信息的RRT像无头苍蝇，探索空间完全靠运气，如下图

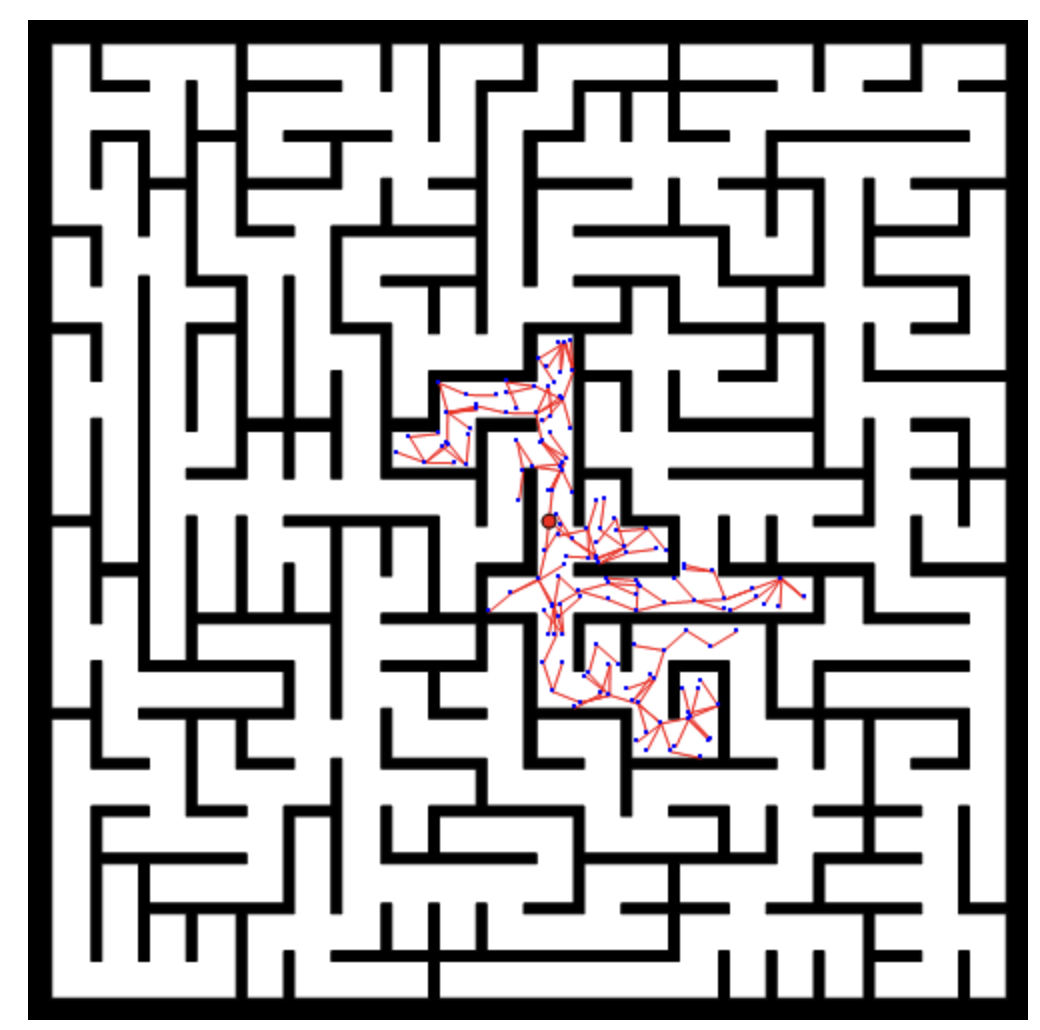
针对上述缺陷，又出现了很多RRT算法的变种，以后的文章中会介绍。

编辑：黄飞