后量子密码的发展趋势研究

摘　要

密码是保障网络通信安全的堡垒，随着量子计算的出现，经典密码体制在维护信息安全方面面临着巨大的挑战。目前，后量子密码算法是理论上证明可保障量子环境下通信安全的新型密码方案。通过分析现有量子计算技术与后量子密码方案设计的研究进展，强调后量子密码研究的紧迫感，表明后量子密码的研究在信息安全中的重要性，最后指出后量子密码下一步可能的研究方向，为我国后量子密码技术研究提供参考。

古有飞鸽，现有网络，在以知识经济为基础的信息化社会中，保障网络信息安全无疑成为国与国之间无形的武器。历史上，图灵发明电子计算机破译了密码机，打破了国家之间信息安全的屏障。此后在经典计算机上，人们通过设计基于数学上 NP 难问题的加解密算法，维护了近 50 年的网络信息与通信安全。但是，1982年 Feynman首次提出将量子力学与计算机相结合的构想，开辟了量子时代的新纪元。1985 年Deutsch进一步阐述了量子计算机的基本概念，并证实了在某些方面，量子计算机相比经典计算机而言确实具有更强大的功能。1994 年 Shor给出了一个能够在多项式时间内解决大整数分解和离散对数问题的 Shor 量子算法。至此，人们察觉到在功能强大的量子计算机面前，现有密码技术搭成的“城墙”是如此的“不堪一击”，因此设计研究能够抵抗量子计攻击的下一代加密算法也变得迫在眉睫。

1

量子计算机的发展现状

20 世纪后期，量子计算机作为量子力学与计算机技术相结合的重要成果而备受国际关注。鉴于其具有实际的战略意义，世界各国都高度重视并不断加大投入，通过陆续制定各种政策、建立一系列的研究机构、启动各类项目来支持量子计算机的研究，推动了量子科技研发和技术产业的蓬勃发展。美国政府在此领域率先行动，斥巨资推出了 5 个专门针对量子计算机的研究计划，分别是由美国国防高级研究计划局提出的“量子信息科学与技术发展规划”、由美国国家安全局指导的 ARDA5 计划、以美国科学基金会为依托的 QuBIC 计划、由美国宇航局领导部署的 QCTG 计划以及美国国家标准与技 术 研 究 院（National Institute of Standards and Technology，NIST）指挥的PLQI计划。除此之外，欧盟、加拿大、中国等组织、国家和地区在量子计算机领域的研究也做出积极响应并取得了一系列的研究成果。

2001 年， 一 个 由 IBM 公司成功研发的 7qubit 的示例性量子计算机成功领跑了该领域的研究。2007 年，中国科学家潘建伟首次在量子计算机上实现了 Shor 量子分解算法 ，该成果标志着中国光学量子计算机的研究在国际上已经达到了先进水平。2008 年，加拿大的 D-wave公司对已有量子计算机系统进行改进并成功将运算位数提高到 48 qubit。2010 年，英国布里斯托尔大学开发出了一种新的光子芯片，该芯片速度更快、存储量更大，为量子计算机的信息存储提供了新的思路。同年，潘建伟团队与清华大学组成的联合小组通过研究量子隐形传态技术的特点，成功实现了世界上最远距离的量子传输 并将该研究成果发表在国际权威杂志 Nature Photonics 上，该成果向全球展示了基于量子计算机的量子通信网络实现的可行性。与此同时，杜江峰教授在 Nature 上发表了一篇关于保持固态自旋比特的量子相干性研究的论文，该成果对固态自旋量子计算机的实现具有重要意义。后来，英国和澳大利亚的联合研究小组设计了一种称为 FTQC 的容错量子计算方案，该方案的提出奠定了量子计算机走向实用化的基础。

随着量子计算技术与硬件设备材料的飞速发展，人们愈发坚信量子计算机走向现实欠缺的不再是技术原因，而是时间的沉淀，借此各国加快针对量子计算机的研究脚步。2016 年，中国在“十三五”规划中明确设立关于“量子通信与量子计算机”的重大科研项目 。同年，Shor 量子分解算法成功运行在潘建伟团队研究的光量子计算机上，为纪念这一研究成果，发射了国际上第一颗名为“墨子号”的量子卫星。2017 年，潘建伟团队自主研发的 10 bit 超导量子线路样品成功实现了当时世界上最大数目的超导量子比特纠缠和完整测量，在量子计算机的发展道路上又迈上了一个新的台阶。2018 年，欧盟正式启动“量子技术旗舰计划”，该计划拟在欧洲建设一个连接所有量子计算机、模拟器与传感器的量子通信网络 。2019 年， 谷歌团队在量子计算原型机“悬铃木”上仅用了3 分 20 秒就完成了超级计算机一万年计算量的工作，该成果将量子计算机的处理能力又带向新的高度，一定意义上实现了量子霸权。2020年，美国白宫网站发布的《美国量子网络战略构想》提出，开发一种由量子计算机和其他量子设备组成的量子互联网的设想，并指出下一步的工作是使量子信息科学全民化。2021 年，中国提出了新的“十四五”规划，指出这 5 年是中国量子技术实现“弯道超车”的关键时期，其目标之一就是研制通用量子计算原型机和实用化量子模拟机 。同年 10 月，潘建伟团队与其他研究机构合作，成功构建了 113 个光子 144 种模式的量子计算原型机“九章二号”，实现了在高斯玻色取样数学问题上的快速求解。除此之外，潘建伟团队及其合作伙伴还成功研制出了66超导量子比特的“祖冲之二号”，相比于“悬铃木”，在计算复杂度方面提高了 6 个数量级。2022 年，Huggins 等人在 Nature 上发表文章，将 QMC 方法与量子计算相结合，构建了混合量子经典计算模型，提供了一条实现实际量子优势的途径，为实用化量子计算机的设计提供了理论基础。

量子计算机的快速发展减少了高计算量问题的处理时间，解决了大量复杂的数学问题，给当前已经发展成熟并且应用广泛的现代公钥密码体制带来了巨大的威胁与严峻的挑战。然而，保障量子计算机下网络安全与信息系统安全的重点在于密码技术的发展，因此，在量子信息时代来临之前，设计能够有效抵御量子计算机攻击的新型密码体制就成了密码学家们不得不面对的问题之一。

2

抵御量子威胁时不我待

2.1　抵御量子威胁的战略意义

密码技术是维护信息安全的重中之重，大量应用于国家保密系统和大型国防装备。一旦量子计算机问世，现代密码学中基于大整数分解、离散对数问题设计的公钥密码将被攻破，直接威胁到当前党政军民领域的网络与信息安全，甚至威胁国家安全。

在军事方面，“先存储后破译”是破解当前密码系统的一个重要战略，即一些组织将现在无法破译的信息先存储起来，等到日后时机成熟再进行破译，如果按照“摩尔定律”的规律来看，这个成熟的时机很可能在非常长的时间内都不可能来临，而量子计算的出现，加快了成熟时机的到来，对长期保密性以及前向安全性都造成了致命的威胁。通常，在国家军队与许多重要机构的设备中存储了大量的国家安全情报，这些情报需要保存十几年甚至更长的时间不能被破解，由此可见，量子计算的出现将直接威胁到国家重要情报的安全，因此必须尽快研制出能够抵抗量子计算机的新型加密体制，以最大限度地解除该隐患。

在日常通信方面，许多关键的通信协议大多以公钥加密、数字签名和密钥交换为依托，然而这些公钥密码学算法基于的特定数论难题的困难性在量子计算面前“不值一提”，一旦量子计算机实用化，这些通信协议将纷纷变得不再安全，无法保障端到端的安全传输。

2.2　密码算法的实用化需要时间孵化

任何一个密码算法的设计都是为了最终迁移到工程化。从现代密码算法理论技术发展成熟到最终的标准化，人们花费了近 20 年的时间才构造出一套完整的公钥密码系统基础设施。即使新型密码算法的理论技术已经发展成熟，但将现在广泛应用的密码系统逐步转化为能够抵抗量子计算机攻击的新型密码系统也需要大量时间，更何况现在能够抵抗量子计算机攻击的新型密码算法的理论技术还未发展成熟。因此，不管量子时代何时到来，尽快采取行动设计新型密码方案，保障量子计算机信息与通信系统的安全都十分必要。

3

全球守护量子时代下的信息安全

沿袭经典计算机中设计公钥密码算法的思路，目前国际上应对量子计算机攻击的后量子密 码（Post-Quantum Cryptography，PQC）算法主要集中在寻找一类或多类在量子计算机上多项式时间内不可解的数学困难问题。根据这些困难问题设计出的 PQC 算法可以在一定程度上抵抗量子计算机的攻击，守护量子信息时代下的通信安全。全球针对 PQC 算法的研究主要集中在两个方面：国际学术交流和算法标准化的建立。

3.1　后量子密码理论的国际学术交流

作为密码学领域的分支，国际 PQC 理论和技术的研究一直以来都受到了各国关注，相关的学术交流活动的数量和频度逐年递增，其影响范围向更多的国家和领域辐射。

2006 年， 国 际 密 码 研 究 协 会 举 办 了 第 一届后量子密码技术国际会议，该会议讨论了PQC 在未来的研究中可能存在的潜在领域。此后，这项会议分别在北美、欧洲、东亚等多个地区连续举办，并通过在相邻会议间隙举办夏季或冬季培训营的方式，促进了各国研究者之间的交流，增强了 PQC 技术的发展。

2011 年， 美 国 安 全 创 新 公 司 注 册 并 拥 有NTRU 算法的专利，自此，该公司设计并开发了多种 NTRU 算法实现的软件库。2013 年，欧洲电信标准协会与加拿大滑铁卢大学量子计算中心联合举办了量子安全密码工作组会议（IQC/ETSI Quantum-Safe Crypto Workshop），参会代表来自密码学、数学、物理学、计算机等多个不同的研究领域，目标是部署下一代密码基础设施，特别是抵御量子计算带来的冲击。2015 年 1 月，欧盟启动 PQC 算法 SAFECRYPTO 应用项目。借助欧洲多所企业、高校和研究机构的力量，相继开展了 PQCRYPTO 项目 和 PROMETHEUS 项目，并将 PQCRYPTO 项目纳入欧盟地平线 2020计划，致力于打造新一代安全实用的 PQC 方案。2016 年 4 月，微软公司开发出了基于格上的困难问题 RLWE 的格密码库（Lattice Crypto），微软公司表示攻击者无论是使用经典计算机还是量子计算机，该软件库至少能够实现 128 位的安全性能。同年 7 月，谷歌公司宣布将开始进行 PQC 技术的测试活动，并表明本次测试对象为基于RLWE问题的密钥交换协议。2019年1月，谷歌宣布将部署一种称为组合椭圆曲线和后量子密钥交换（CECPQ2）的新的传输层安全性协议（Transport Layer Security，TLS）密钥交换方法。同时，谷歌和 Cloudflare 将合作探索 PQC 如何在实践中击败超文本传输安全协议（Hypertext Transfer Protocol Secure，HTTPS）连接。2022 年4 月，IBM 公司发布了首个基于格理论研发的量子安全系统——IBMz16。

亚洲密码学研究者在后量子相关技术的发展中也在积极跟进。2016 年 6 月，首届亚洲后量 子 密 码 论 坛（PQCAsia Forum）在我国成都顺利召开。鉴于 PQC 算法的飞速发展，原定于2017 年召开的第二届亚洲后量子密码论坛提前到 2016 年 11 月于韩国首尔大学召开。2020—2021 年，丁津泰所带领的团队先后破解了两个NIST 抗量子数字签名候选方案，包括 Luov 和GeMMS，并将研究成果发表在 2020 年“欧洲密码学年会”和 2021 年“美国密码学年会”上。2022 年，上海交通大学的谷大武教授领导的LoCCS 实验室成功破解了 80 维格的容错学习问题（Learning With Errors，LWE），创造了格密码中困难问题求解新的世界纪录，同时该纪录已经在格密码挑战的官方网站 LWE Challenge上进行了公布。

3.2　后量子密码方案的标准化建立

目前，全球已经有众多国家意识到未来量子攻击对网络安全带来的潜在威胁，也已采取必要行动和相关部署来应对此威胁。类似于现代密码学中 DES、AES、RSA、ElGamal 等加密算法标准，在 PQC 理论的研究过程中，标准化的建立也逐步发展起来，越来越多的国际参与者纷纷加入 PQC 方案标准化建立的研究中。

3.2.1　美国后量子密码标准化计划

早 在 2008 年，NTRU 加密算法就已经被美国电气和电子工程师协会确定为正式标准（Std1363.1—2008）。2010 年，其又被认可标准 委 员 会（Accredited Standards Committee X9）批准为可用于数据防护的新型加密标准。同时，美国国家标准学会 X9.98 标准（ANSIX9.98）明确了在金融交易过程中如何使用基于诸如 NTRU等格加密算法的公私钥加密系统。

2015 年 8 月，美国国家安全局宣布对当前美国政府所使用的“密码算法 B 套件”进行安全性升级，升级的算法将用于后量子时代过渡期的加密标准。2016 年 4 月，NIST 颁布“后量子密码学”研究报告 ，并宣布将启动 PQC算法标准计划。截至 2017 年 12 月，NIST 共收到来自全球共 82 份候选密码方案，自此开启了后量子密码学标准协议的第一轮预选。2019年 1 月，NIST 揭晓第二轮的标准方案，本轮共有 26 个密码方案脱颖而出，其中包括 17 个公钥加密 / 密钥交换方案和 9 个数字签名方案。按照密码方案的构造方式来看，这 26 个候选算法中包括 12 个格密码，7 个基于编码的密码，4 个基于多变量的密码，2 个基于哈希的密码和1 个基于同源曲线的密码。2021 年 1 月，NIST公布的第三轮候选算法中包括 7 个决赛入选方案和 8 个备选方案，在这 7 个决赛入选方案中，有 5 个都是格密码，这说明当前格密码在所有的 PQC 算法中占据较大的优势，是未来最有望成为标准化的算法。2022 年 3 月，麻省理工学院与阿布扎比技术创新研究所合作编写并出版了《从今天起，直面明天的量子黑客》（Facing Tomorrow’s Quantum Hackers Today）。该报告对全球量子计算公司中的密码学家、数学家、物理学家和高级管理人员进行采访，评估了一台成熟的量子黑客计算机对如今网络安全系统的威胁与影响，并在此基础上分析了应对威胁的解决方案，这意味着 NIST 标准化即将进入第四轮。2022 年 7 月，NIST 已完成第三轮 PQC 标准化过程，共有 4 个候选算法被选中标准化，分别是 CRYSTALS-KYBER、CRYSTALS-Dilithium、FALCON 和 SPHINCS+，另外还有 4 种算法将继续进入第四轮，这一里程碑事件意味着持续6 年的标准化工作终于进入了最后阶段。

3.2.2　欧洲后量子密码标准化计划

首先，在 NIST-PQC 算法的征集过程中，欧洲研究团队做出了重大的贡献，在 NIST 发布的第二轮 26 个标准方案中，欧洲主导和参与的高达 20 多个。其次，欧洲量子密码学术和工业界研究者联合组织的 PQCrypto 项目于 2015 年发布了一份初始报告，该报告在加密算法、对称授权以及签名系统等多个领域都提出了相关的标准化建议，并指出 McEliece 密码系统具有发展成为替代 RSA/ECC 密码系统的潜力。此外，欧洲电信标准协会 ETSI 成立的“量子安全密码工业标准工作组”主要负责 PQC 算法的征集、评估以及工业标准的制定，该组织每年发布一本“量子安全白皮书”，用以公布后量子密码研究的最新进展。

3.2.3　日本后量子密码标准化计划

为应对量子计算攻击和对加密设备的物理攻击（例如功率分析），日本推出了 CREST 密码数学项目，旨在为下一代加密系统的开发奠定基础。CREST 项目每年举办的后量子安全的相关会议，为日本后量子密码学研究者交流重要成果提供了平台。在真正的 PQC 标准公布之前，日本密码研究与评估委员会列出了 3 个密码清单：电子政务推荐密码清单、候选推荐密码清单和监控密码清单，并指出将启动最新制定的 PQC 指南。

3.2.4　韩国后量子密码标准化计划

为及时跟进国际后量子标准化工作，韩国于 2022 年推出了全球首个可防御量子计算机黑客攻击的 PQC 专线，目前，该线路已经过电信技术协会的测试和验证。

3.2.5　中国后量子密码标准化计划

虽然中国在PQC标准化的研究中起步较晚，但在 NIST-PQC 算法征集活动中也参与并贡献了一定的力量。参与设计的中国团队包括密码科学技术国家重点实验室、上海交通大学、复旦大学、中科院信工所以及中国台湾地区“中央研究院”等。其中，由中国科学院数据与通信保护研究教育中心设计的 LAC 算法，与欧洲、美国、加拿大等国家提供的 PQC 算法一起，入选了 NIST 第二轮 PQC 密码算法名单。除此之外，中国在国内 PQC 算法标准的征集活动中也做了一些工作。自 2019 年起，中国密码学会（Chinese Association for Cryptologic Research，CACR）开始举办全国密码算法设计竞赛 ，该竞赛仅面向中国的密码学者，受到了广大密码学家的青睐，并在公钥密码组的参赛作品中征集到大量的 PQC 算法。该竞赛的成功举办推动了我国密码理论与应用技术的发展，是我国在 PQC 算法标准制定过程中的基础，意味着我国 PQC 技术的研究正逐步向国际先进水平看齐，致力于通过充分调动国内各界研究力量，推动国产化研发，保障未来后量子时代下我国的网络空间安全。

综上所述，从世界各国政府对该领域的投入与支持力度来看，在真正的量子信息时代到来之前，全球的目标均是在量子通信网络中实现保密通信与安全认证。

4

后量子密码的构造方式

在 PQC 算 法 的 设 计 方 案 中， 大 多 还 是 基于数学困难问题的难解性，目前主流数学困难问题主要包括格、编码、哈希以及多变量。除此之外，基于超奇异椭圆曲线、量子随机漫步等技术的 PQC 构造方法以及较大密钥长度的对称密码算法也被认为是量子计算机条件下相对安全的。

4.1　基于格的后量子密码算法

格（lattice）是一种数学结构，定义为一组线性无关的非零向量（称作格基）的整系数线性组合。具体来说，给定一组格基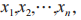对任意的整数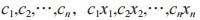都是属于这个格的向量，其中 n 称为格的维数。对于同一个格，其可以拥有不同的格基，并且求解格中的最短向量问题（Shortest Vector Problem，SVP）和最近向量问题（Closest Vector Problem，CVP）是目前格理论中主要的非确定性多项式难题（Nondeterministic Polynomially problem，NP）。除此之外，格中还有一些其他的困难问题，比如 LWE 问题、有界距离解码问题、小整数解问题、gap-SVP 问题等，因此，基于格的 PQC 算法大多依托这些困难问题而设计，但其本质上又都可以转化为 SVP 困难问题和 CVP 困难问题。基于格的算法与现代公钥加密算法的功能一样，均可实现加解密、数字签名、属性加密、同态加密、密钥交换等多种密码学构造。

第一个基于格的密码方案是 1997 年由 Ajtai等人提出的 Ajtai-Dwork 密码体制，该方案利用格问题中 Worst-case 到 Average-case 的规约来抵抗量子计算的攻击。第一个基于格的实用的密码方案是 1998 年由 Hoffstein 等人提出的 NTRU 公钥加密体制，该方案坚持到了 NIST第三轮的候选算法中，并且目前已经应用在某些商用的密码设备中，有望日后代替 RSA 加密算法。

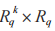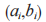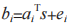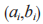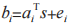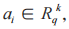在后量子加解密算法方面，通过总结目前主流的基于格的加解密算法，我们发现以 LWE困难问题为基础的格密码方案不仅应用广泛，而 且 安 全 性 更 高。以 NIST 第四轮入选算法CRYSTALS-Kyber 为例，该算法基于的困难问题是 M-LWE 问题，即 LWE 问题与 R-LWE 问题的组合，该问题相比于 LWE 问题而言具有易于扩展和效率高的优点。M-LWE 问题的主要思想是对于在多项式环中均匀随机选取的与经过公式计算得到的 是不可区分的，其中中s 和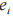是从二项分布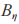中随机均匀选取的，该问题的主要困难性在于根据已知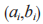无法计算 s 和 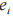中的任意一个。Kyber 算法就是利用此原理，通过公式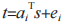生成公私钥对 (t,s)，达到已知公钥 t 后无法计算私钥 s 的效果，此后再对通信的明文信息进行加密或者对通信双方的临时会话密钥进行封装。以 2020 年提交的第三版 Kyber算法为例，表 1 阐述了选择明文攻击下的不可区分性（IND-CPA）安全的 Kyber 算法的具体实现思路，表 2 阐述了自适应选择密文攻击下的密文不可识别性（IND-CCA2）安全的 Kyber 算法的具体实现思路。

表 1 　Kyber 算法实现过程（IND-CPA 安全）

表 2　 Kyber 算法实现过程（IND-CCA2 安全）

在后量子签名算法方面，基于格的签名算法的构造与现有的公钥密码体制略有不同。对于 RSA、ElGamal、椭圆曲线等现有公钥密码体制而言，通过调换加解密算法的公私钥顺序即可将其转换为签名算法；但是基于格的密码方案不具有此种对偶特性，在设计基于格的后量子签名算法时通常采用零知识证明协议进行构造，即证明者证明自己拥有与对应身份的公钥相匹配的私钥，但是不泄露任何关于私钥的信息。

2008 年，Gentry 等人提出了 GPV 框架，该框架指出了基于格的签名算法的设计思路，如表 3 所示。

表3　GPV 框架

以 GPV 框架为基础，基于格的签名算法在进行公私钥对生成的过程中底层基于的困难问题与后量子加解密算法类似，即 LWE 问题和SIS 问题，同时为了便于签名算法的实现，设计方案时大多借助 NTRU 格实例化 GPV 框架，并通过采样完成数字签名的创建，比如进入 NIST第 四 轮 的 签 名 算 法：FALCON 算 法。除 此 之外，另一个比较受欢迎的签名算法 CRYSTALSDilithium 也进入了 NIST 的第四轮中。

在具体的设计过程中，CRYSTALS-Dilithium和 FALCON 两个算法针对算法本身的安全性和算法的运行速度分别进行了不同的改进。其中 CRYSTALS-Dilithium 签名算法在设计时采用Fiat-Shamir with Aborts 技术，该技术使用拒绝采样的方式将基于格的 Fiat-Shamir 方案变得更加紧凑且安全；由于传统的签名算法中高斯采样难以高效且安全地实现，Dilithium 签名算法改进了采样方式，仅通过均匀分布采样就完成了签名的创建；同时为减小公钥的大小，Dilithium签名算法采用分离高低阶位的新技术将其缩小了两倍以上。对于 FALCON 签名算法，通过在采样过程中应用快速傅里叶采样技术，并在算法内部使用真正的高斯采样器，由此保证了在无限签名情况下 FALCON 算法的安全性，即密钥信息的泄露可忽略不计；同时由于快速傅里叶采样在实现过程中具有速度快的优势，使得FALCON 算法在普通计算机上每秒可以生成数千个有效的签名，并且验签过程相比其他签名算法而言快将近 5~10 倍。关于 Dilithium 和 FALCON签名算法的具体过程分别如表 4 和表 5 所示。

表 4　Dilithium 签名算法的实现过程

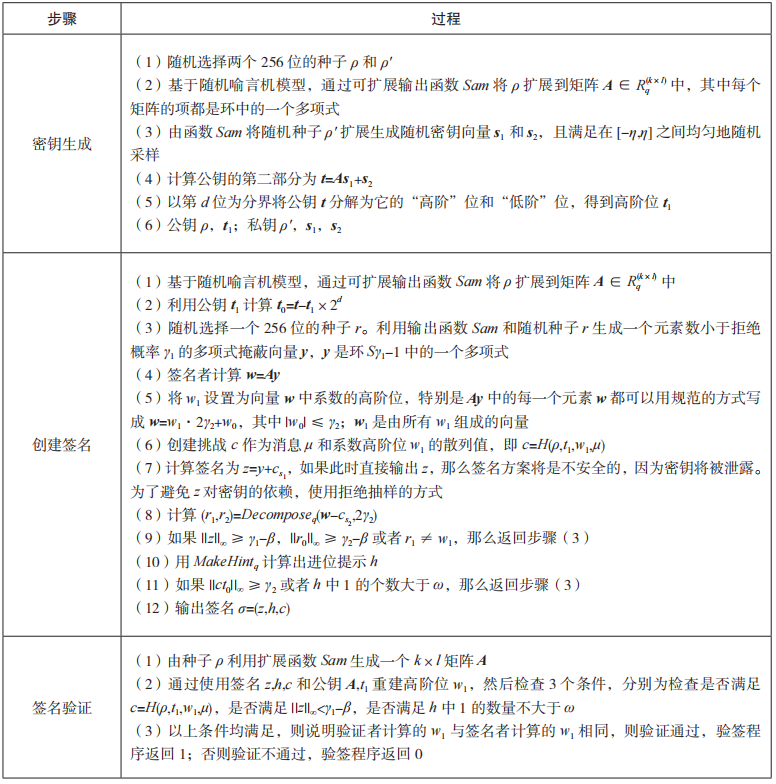
表 5　FALCON 签名算法的实现过程

格密码的研究虽然起步较晚，但是其简单的结构以及众多高复杂度的数学困难问题使其在后量子时代广受各国学者的欢迎。自 2013 年起，格密码的研究成果显著增加，在基于格的密码体制不断改进的过程中，密钥尺寸不断缩小、运算速度不断提高，逐步在安全性、密钥尺寸以及计算速度上达到更好的平衡。2022 年7 月入选 NIST 第四轮的后量子密码中有 3 个基于格设计的密码方案，由此足以见得尽管格密码仍处于发展阶段，但目前其已经被认为是最有前景的后量子密码算法之一。

4.2　基于编码的后量子密码算法

编码理论是数学与计算机科学的一个分支，用来处理在噪声信道中传送信息时进行错误处理。基于编码的密码体制也被认为是在量子计算机中相对安全的密码算法，其核心在于将一定数量的错误码字引入编码中，纠正错误码字或计算校验矩阵的伴随式是困难的。

一个较早提出且至今使用的基于编码的加密算法是 1978 年 McEliece[27] 提出的 ClassicalMcEliece 公钥加密方案，该方案使用随机二进制不可约的 Goppa 码作为私钥，记作 A，对私钥 A使用可逆矩阵 S 和随机置换矩阵 P 进行 A'=SAP变换后得到的一般线性码A'作为公钥的一部分。最终 McEliece 公钥加密方案的公钥由 Goppa 码的汉明重量 t 和矩阵 A' 组成，私钥由生成矩阵A、可逆矩阵 S 和随机置换矩阵 P 组成（方案的整体流程如表 6 所示）。该方案基于的困难问题是对称群隐藏子群问题，也就是在加密过程中对明文信息 x 进行的 y=y'+e=x×A'+e 操作中，从加入混淆 e（带有 t 个错误的向量）的矩阵 A'中反推 Goppa 码是困难的。该算法相对于现有公钥密码体制而言加密速度快，但是由于其公钥尺寸过大，该算法并不是很实用化，不过针对该算法的改进最终也进入到了 NIST 第三轮的候选算法中。

表 6 McEliece 公钥加密方案过程

此后，1986 年 Niederreiter 提出了一种基于GRS 码的背包型公钥密码体制——Niederreiter密码算法，该算法与 McEliece 不同的地方在于在密钥生成过程中，当确定私钥 A（生成矩阵）后，借助可逆矩阵 M 和置换矩阵 P 通过 A'=MHP操作来隐藏校验矩阵 H 而非生成矩阵 A，从而生成算法的公钥 A'。为证明 Niederreiter 密码算法的安全性，1994 年，王新梅等人  证明其在安全性方面与 McEliece 是等价的。

针对基于编码的数字签名方案而言，王新梅于 1990 年提出了第一个基于编码的 Xinmei数字签名方案。次年，李兴元构造了一类同时具有签名、加密和纠错能力的公钥体制。随后，学者们在此基础上进行了一系列的改进，并指出基于编码的公钥密码体制或许可以成为基于数论的公钥密码体制的一个很好的替代。

4.3　基于哈希的后量子密码算法

基于 Hash 函数设计的后量子密码算法主要集中在数字签名算法中，Hash 函数具有一个很好的性质就是抗碰撞性，当 Hash 函数能抗强碰撞时，设计的数字签名算法便可有效抵抗量子计算的攻击。在基于 Hash 函数的数字签名算法中，具有代表性的是 1989 年 Merkle 从一次性签名方案出发，借鉴 Lamport 和 Diffie 的工作，发明的 Merkle 数字签名方案（MSS）。MSS 的基本思想是利用 Hash 树将多个一次性验证密钥（Hash树的叶子）的有效性降低到一个公钥（Hash树的根）的有效性。由于其良好的抗强碰撞性，使得其可以有效抵抗量子计算的攻击，因此，MSS 受到了学者们的青睐。从 2006 年举办的第一届国际后量子密码会议开始，就不断有人提出针对 MSS 的改进，例如 2006 年，Michael Szydlo提出了一种使 Merkle 树的构建更加有效和实用的方法；2008 年，基于 Szydlo’s 算法，JohannesBuchmann 等人提供了一种计算数字签名机制中认证路径的新方法，并大大减少了最坏情况下算法的运行时间；2011 年，Buchmann 等人 在 MSS 的基础上提出了一种具有更小签名的可证明安全的 XMSS 数字签名方案。

在 MSS 的 研 究 之 外，2016 年，Targhi 等人估计出了寻找一个函数碰撞的量子查询复杂度。2017 年，SPHINCS+ 算法被提交到 NIST PQC 竞赛中，经过层层筛选，该算法进入到了NIST 第三轮候选算法中，后续通过进一步的安全性分析，该算法在 NIST 第四轮评估中脱颖而出，成为正式候选的签名算法之一。SPHINCS+签名算法采用了一种被称为 SPHINCS 超树的结构进行构造，SPHINCS 超树是一种在 Merkle 树和 Goldreich 树之间相折中的结构，其外层结构是一个 k 叉树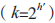，一共有 d 层；k 叉树的每个节点是一个高度为 h' 的 Merkle 树，Merkle树的每个子节点是一个密钥，其中叶子节点用来给外层结构的子节点生成公钥，非叶子节点用来给 FORS 密钥生成公钥；外层结构的叶子结点也是 Merkle 树， 用 来 给 消 息 进 行 签 名。SPHINCS+ 签名算法通过一个伪随机数生成器和一个随机种子构造一个 SPHINCS 超树，然后根据 SPHINCS 超树生成公私钥对。在进行消息签名时，首先计算消息 m 的哈希值 H(m)，然后取出 H(m) 的 h 个比特用来确定使用哪一个 FORS密钥，再取出 kα 个比特用于 FORS 签名，最终将 SPHINCS 超树从叶子节点到根节点连在一起的签名链作为消息 m 的签名。在进行签名验证时，接收者依次验证签名链上的每个签名即可。

尽管目前基于 Hash 函数的数字签名方案成果并不多，但是考虑 Hash 函数独特的属性及其实用性，在量子时代，基于 Hash 函数的签名算法有望成为最有前途的数字签名方案之一。

4.4　基于多变量的后量子密码算法

作为后量子密码算法的最早成员之一，基于多变量的后量子密码算法相比其他 3 种主流构造方式而言具有更多的研究成果。一个基于多变量的公钥密码系统将有限域上一组二次多项式作为它的公钥映射，其主要安全假设为求解有限域上非线性方程组这个 NP 难问题。

最早的多变量公钥密码体制由 Matsumoto 等人 于 1988 年提出，在随后的 20 多年时间里，诸如清华大学丘成桐数学科学中心的丁津泰、日本的 Kohtaro Tadaki 和我国台湾地区的 Bo-Yin Yang 等很多知名学者在多变量公钥密码领域展开激烈讨论并取得了不错的研究成果。2010 年以来，学者们针对多变量公钥密码体制的研究主要集中在 3 个方面：对包括加密、签名等方案中基本理论的深入研究与改进优化，对类似全同态加密（Fully Homomorphic Encryption，FHE）等热点领域的重点攻关，对全新算法设计结构的尝试与探索。据统计，自 2006 年起，在全八届国际后量子密码会议收集的论文中，有 39%的论文是针对多变量密码算法的设计与改进[36]，远远高于基于其他方式设计的后量子密码算法，由此可见多变量公钥密码体制在后量子时代的地位和意义。

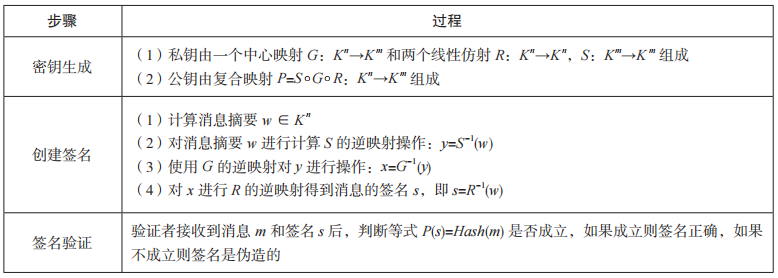
在 众 多 的 多 变 量 公 钥 密 码 体 制 中， 进 入NIST 第三轮的多变量签名算法就是由丁津泰教授于 2005 年设计的 Rainbow 数字签名算法。该算法由于采用相对小的有限域以及基础的逻辑运算而具有较高的运算速度，同时该算法相较于其他签名算法而言因其较短的签名长度而更为实用。该算法采用非平衡油醋（Unbalanced Oil and Vinegar，UOV）体制创建签名，核心是一个多层的 UOV 结构的中心映射。UOV 体制是油 醋（Oil and Vinegar，OV） 体 制 的 扩 展，OV体制在签名过程中随机选取一组醋变量代入油醋多项式中，然后结合签名消息 m 求解一个关于油变量的线性方程组，而 UOV 体制是一种多层的油醋体制，即每一层都是油醋多项式，而且上一层的所有变量是下一层的醋变量。Rainbow数字签名算法的具体流程如表 7 所示。

表 7 Rainbow 数字签名算法的实现过程

Rainbow 签名算法自 1999 年起一直经受各种密码分析，例如 MinRank 攻击，HighRank 攻击，Billet-Gilbert 攻击等 。直到 2022 年，Beullens再次对 Rainbow 签名算法进行了进一步的改进，并表明对于给定的 NIST 第二轮提交的 SL 1 参数集的公钥，通过密钥恢复攻击，在标准笔记本电脑上平均 53 小时即可返回相应的密钥。

尽管在 NIST 第四轮的标准化候选算法中没有多变量公钥密码体制，但是在某些注重算法效率的应用场景中，多变量公钥密码体制或许会进入一个新的高度。

4.5　其他后量子密码算法

除上述 4 种主流算法外，基于量子密码和基于同源的密码体制也在密码学家的研究范围内。2012 年，Kashefi 等 人提出了量子单向函数的候选方案，Mosca 等人研究了经典认证密钥交换框架下量子密钥的分配问题。2006年，Couveignes介绍了困难的同质空间（Hard Homogeneous Spaces，HHS）的概念并延伸介绍了相关理论，为基于椭圆曲线同源的密码系统奠定了基础。同年，Rostovtsev 等人 提出了一个新的适用于公钥密码系统的通用数学问题：对于有限域上的椭圆曲线，计算给定椭圆曲线之间的同源（代数同态），与此同时，ElGamal公钥加密和 Diffie-Hellman 密钥协议被提出用于同源密码系统。2014 年，Jao 等人 公布了一个在椭圆曲线同源基础上不可否认的数字签名方案。2017 年，Gélin 等人  和 Ti分别对超奇异同源密码系统的循环终止故障攻击和第一类 故 障 攻 击 进 行 了 讨 论。2022 年，Castryck、Maino 和 Chi-Domínguez 针对超奇异同源密钥交换协议（SIDH），分别提出了不同的密钥恢复攻击方案。尽管这些后量子密码算法并未像其他主流算法一样形成体系，但是在不久的将来，这些后量子密码算法或者其他新的后量子算法也会逐步登上舞台。

5

后量子密码的发展趋势

量子计算机的出现可以看成新一代的技术革命，作为计算机下一轮迭代的发展方向，量子计算机在密码破解、机器学习、量子模拟等多个领域具有得天独厚的优势，日后量子计算机也极有可能成为人们日常生活中的一部分。后量子密码算法作为应对量子计算攻击的新型密码方案，研究时间不过短短 30 年左右，仍有许多问题亟须探索。

5.1　经典后量子密码算法的优化与拓展

量子计算的发展对密码技术提出了更高的要求，同时也促成了密码分析技术的进步。尽管目前已经设计研究出众多类型的后量子密码算法，但是针对这些密码算法的理论攻击仍然存在，例如面向 NIST 第三轮入选算法中 Kyber 的密钥不匹配攻击等，因此在未来对已有的后量子密码算法的改进之路仍需继续前行。除此之外，针对算法的实用化改进同样具有重要意义。通过不断优化算法的参数设计，提高算法的运行效率，降低算法的时间复杂度和空间复杂度，使算法在实际应用中发挥作用。

5.2　量子算法与密码算法的结合

量子算法的设计目标是解决某一类特定的问题或者缩短某些算法的运行时间，例如 Shor算法的发明解决了大整数分解问题，Grover 算法的提出提高了搜索的速度，Simon 算法的出现提供了一种求解函数周期的方法。研究量子算法与密码算法相结合的新型算法，一方面，将量子算法应用于后量子密码的设计中可以提高算法的运行效率，增强其可用性；另一方面，将量子算法应用于密码分析方法中可以从某个角度发现算法潜在的攻击可能性，优化算法参数，提高算法的安全性。

5.3　密码算法量子安全性的评估

量子计算中的一些算法已经被证实对经典密码算法存在有效的理论攻击，这种攻击针对后量子密码算法而言是否有效目前还未知。同时，新的量子算法的出现是否会对现有后量子算法造成威胁也同样未知，因此评估密码算法的量子安全性是未来的一个研究方向。

5.4　量子环境下新的数学问题探索

除了目前基于格、哈希、多变量、编码的后量子密码算法，研究设计更多的基于同源曲线或者量子随机漫步的后量子密码算法也是很有必要的。除此之外，研究设计在量子计算机优势外的数学困难问题也是一种新的探索方向。

6

结　语

针对量子计算的发展，美国已经在实施庞大的量子计划，并公开宣布当项目进行到一定程度后便不再向全球公开，意味着我们将无从获知其他各国最新的研究进展，这将在一定程度上影响我国的战略决策。同时，根据量子计算对网络空间安全方面带来的威胁，全球目标统一在抗量子密码的研究上，但是国与国之间还存在一定差距，此后，我国应延续在量子计算、抗量子密码领域的科研计划，缩小与西方的差距，切实保障国家的网络与信息安全。