

C语言实现欧拉角转四元数
电子说
描述
1. 说在前面的话
2. 欧拉角
3. 欧拉角与四元数关系
4. Matlabe 欧拉角转四元数
5. C语言实现 欧拉角转四元数
6. 获取资源
1. 说在前面的话
1)在介绍以下内容之前,我们假设读者已经对复数与2D旋转、3D空间中的旋转、四元数的性质以及四元数与3D旋转等数学理论有一定的阅读理解基础。
2)欧拉角与四元数姿态表示方法是目前工程上最常用的两种方法。欧拉角表示法具有简便、几何意义明显等优点,同时姿态敏感器可以直接测出这些参数,能较方便地求解用这些姿态参数描述的姿态动力学方程。但采用欧拉角的姿态描述方法存在奇点问题,且需多次三角运算。而采用四元数表示方法则可以避免这些问题,因此目前工程上开始采用四元数来描述飞行器运动及动力学方程中的姿态,而在设计控制规律时,由于欧拉角的直观性和几何意义,仍然采用欧拉角描述。
2. 欧拉角
根据欧拉定理,刚体绕固定点的位移也可以是绕该点的若干次有限转动的合成。在欧拉转动中,将载体坐标系转动三次得到导航坐标系。在三次转动中,每次的旋转轴是被转动坐标系的某一坐标轴,每次的转动角即为欧拉角。因此,用欧拉角确定的姿态矩阵是三次坐标转换矩阵的乘积。
最终的姿态矩阵还与三次转动的顺序有关,下面公式采用3-2-1顺序,即按照Z-Y-X轴的顺序旋转(东北地坐标系(对应的载体坐标系前右下)):
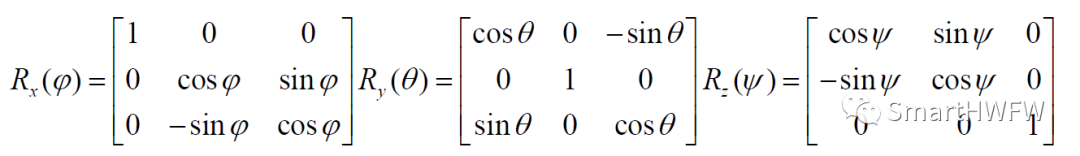
于是可得姿态矩阵
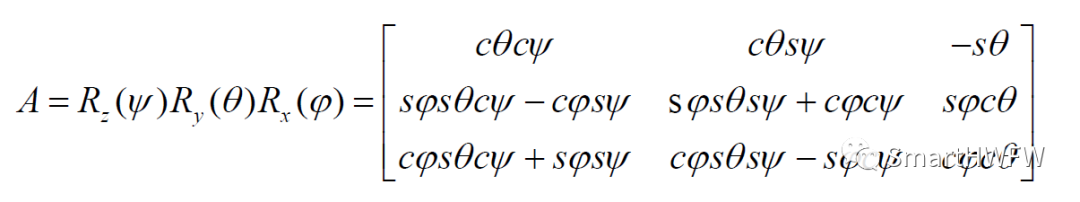
式中,字符"c","s"分别为"cos"和"sin"的缩写形式。
3. 欧拉角与四元数关系
根据四元数的定义,可以将欧拉角式转换为四元数,以欧拉3-2-1转动为例:第一次先绕Z轴转动,φ = θ =0,
四元数表示为:
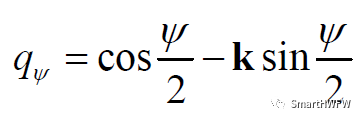
第二次先绕Y轴转动,φ = ψ = 0,
四元数表示为:
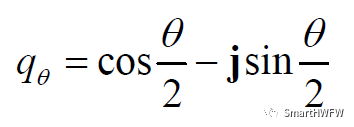
第三次先绕X轴转动,θ = ψ = 0,
四元数表示为:
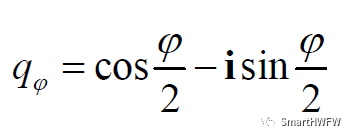
则,绕三轴转动的合成为
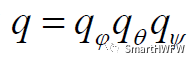
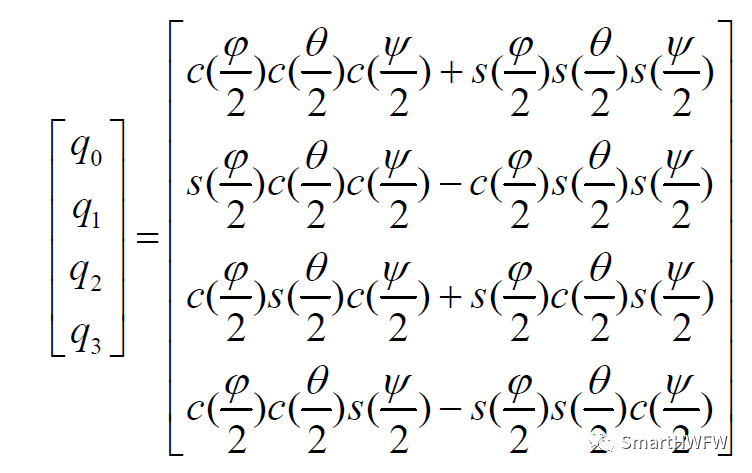
该转换方法在360±°内均有效,是一对一的关系。
4. MATLAB 欧拉角转四元数
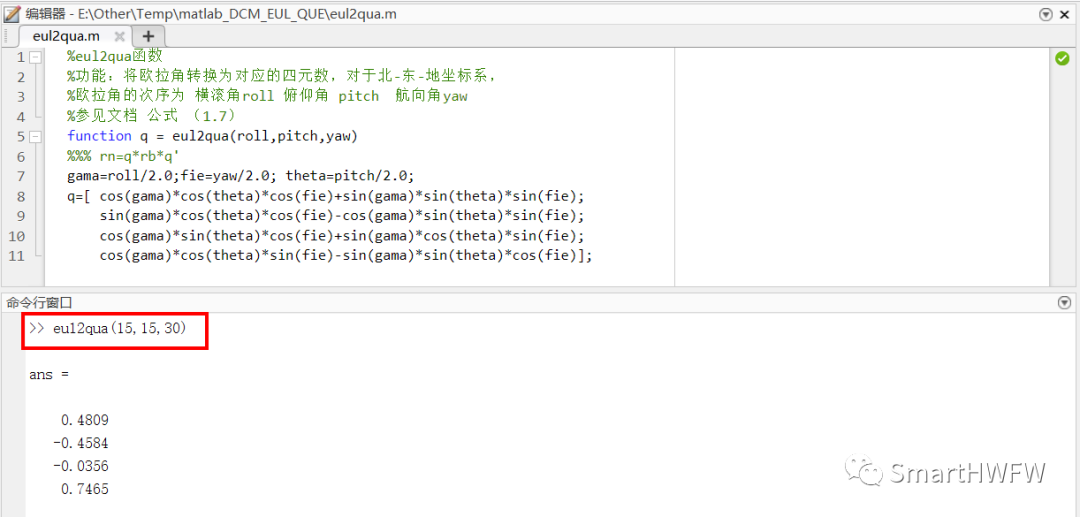
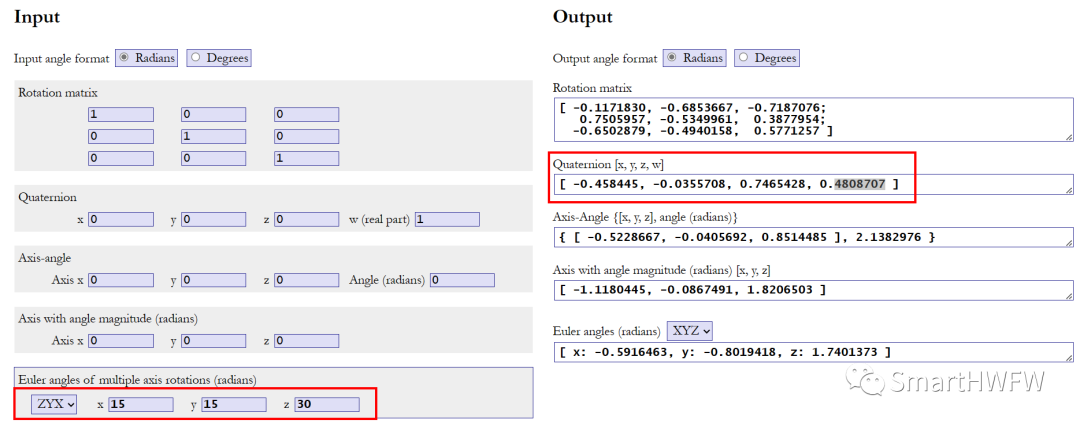
5. C语言实现欧拉角转四元数
欧拉角转四元数的步骤如下:
STEP1:确定每个欧拉角的轴和旋转角度。Yaw对应y轴,Pitch对应x轴,Roll对应z轴。记为yaw_angle,pitch_angle和roll_angle。
STEP2:分别根据每个欧拉角的旋转轴和旋转角度,构造旋转四元数的各个分量。以yaw_angle为例,qw = cos(yaw_angle/2)qx = 0qy = sin(yaw_angle/2)qz = 0
同样地,根据pitch_angle和roll_angle可以得到对应的旋转四元数分量。
STEP3:根据旋转四元数的分量,构造最终的旋转四元数。旋转四元数的分量为(qw, qx, qy, qz)。
请注意,欧拉角到四元数的转换是一个多对一的映射,即不同的欧拉角可能对应相同的旋转四元数。因此,在实际应用中,可能需要根据具体需求选择适合的欧拉角表示方式。
校验结果:
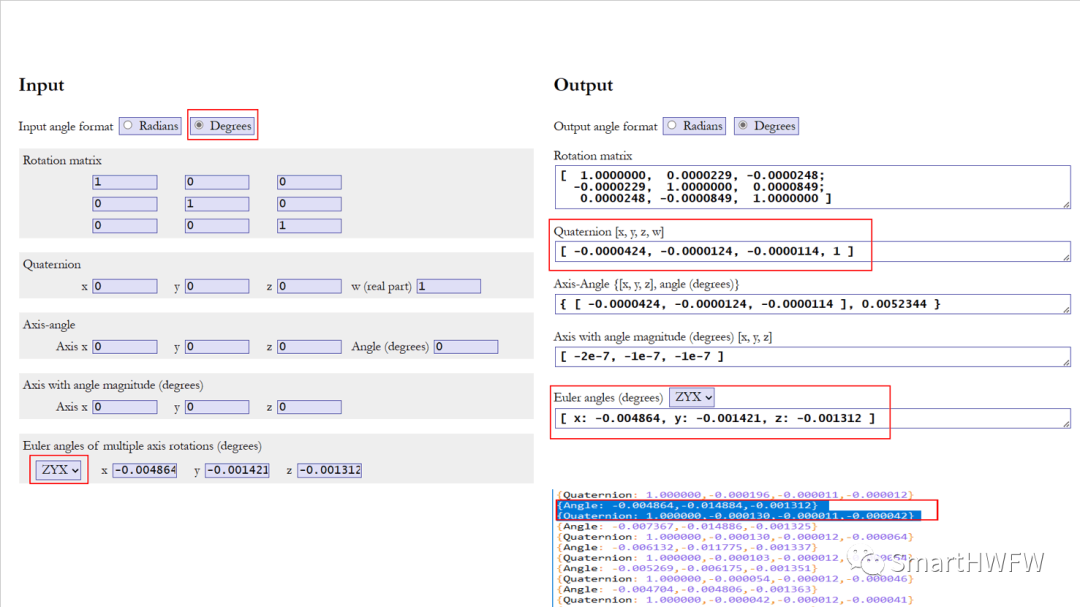
-
四元数与欧拉角之间的转换2016-08-17 2360
-
飞控姿态解算中,欧拉角与四元数之间的转换2016-11-17 6383
-
请问我用四元数转欧拉角造成的这些问题该怎么解决?2019-06-26 4162
-
基于Proteus和C语言实现2021-07-14 943
-
旋转矩阵、四元数、欧拉角比较2015-12-08 671
-
DSP算法的c语言实现2016-05-09 777
-
C++语言实现火车排序功能2017-01-05 702
-
如何使用C语言实现一个比较简单的猜数游戏的程序免费下载2019-04-24 941
-
MPU6050传感器的四元数欧拉角程序免费下载2019-08-30 1357
-
如何将四元数转化为欧拉角2019-12-05 2316
-
使用单片机实现串转并数字芯片测试的C语言实例免费下载2021-03-29 868
-
使用单片机实现PCF8591转换器应用的C语言实例2021-03-31 1141
-
累加校验和C语言实现2021-11-29 815
-
怎么用C语言实现多态2022-10-12 2646
-
使用C语言实现的CRC计算单元的例子2024-05-16 2061
全部0条评论

快来发表一下你的评论吧 !

