

基于Petri网的机车故障诊断方法研究
应用电子电路
描述
1 引言
目前,对于机车故障检查与诊断存在各种方法,其中专家系统,故障树分析方法(fta),以及两者的结合体是被广泛接受的方法,然而,他们也存在一些缺陷;fta仅能表示逻辑关系[1],不能表示动态行为;而专家系统突出弱点就是知识获取的“瓶颈”问题[2];基于故障树的专家系统诊断系统在一些方面虽得到优化,但是由于故障树模型之间的缺陷,又加上诊断的规则数目较多,当添加修改规则时,易出现规则之间的冲突和冗余,无法保证专家系统高效、正确地运行。
在故障检测与诊断领域中,petri网不仅能够用图形符号表示故障事件系统逻辑关系,知识的完成和诊断推理,而且能够表示系统的动态行为,故petri网模型能够用于机车故障检测和可靠性的分析。
在此利用petri网的可达性和状态方程方法,分析故障树信息,解决故障检测和故障传播问题。与基于故障树的诊断方法相比,本文提出的方法具有结构表达图形化、 推理搜索的快速化以及诊断过程的数学化等优点。
2 petri网理论基础及分析
2.1 petri网结构和分析方法
从图形上看,petri网由4种不同类型的元素组成,即库所(place,用“○”表示)、转移(transition,用“|”表示)、连接库所和转移的有向弧及位于库所中的托肯(token,用“·”表示)。库所表示系统状态的逻辑描述,转移表示系统中事件或行为产生过程,输入函数(i)和输出函数(o)分别描述库所和转移之间的联结函数关系。若一库所被赋与k个标记(k为非负整数),则说该库所有k个托肯,也称该库所被标记。于是定义标记petri网为一5元组:
∑=(p,t,i,o,m)。以图1所示petri网为例对上述定义进行具体描述[6]。
∑=(p,t,i,o,m);
p={p1,p2,p3,p4};
m=(1 0 0 0);
i(t1)={p1};o(t1)={p2};
i(t2)={p1};o(t2)={p3};
i(t3)={p2,p3};o(t3)={p4};
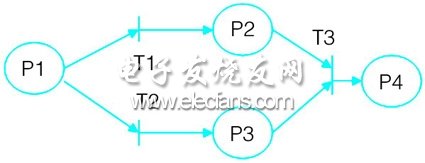
图1 petri网模型
petri网的执行过程受控于网中托肯的数量和分布情况,并通过转移的点火得以实现。一个转移可点火,首先该转移必须允许点火,即转移使能。一个转移使能的前提条件是该转移的每一个输入库所中被标记的托肯数至少等于该所到该转移的有向弧数。也就是说一个转移的所有输入库所中至少包括一个托肯(假设每条有向弧的权均为1)。体现petri网动态行为的启动规则是:若库所代表的条件满足,转移就点火,点火后转移的输入库所的托肯数等于原托肯数减去该库所到转移的输出弧数。转移的点火使petri网的标记由m转变为m’。
关联矩阵和状态方程是petri网分析和建模的主要工具,状态方程的表示为
m=m0+ct*uo
m,m0分别点火前后的初始标识集和结果标识集;ct为关联矩阵,u为点火序列,由0,1组成的n×1列矩阵。
1 引言
目前,对于机车故障检查与诊断存在各种方法,其中专家系统,故障树分析方法(fta),以及两者的结合体是被广泛接受的方法,然而,他们也存在一些缺陷;fta仅能表示逻辑关系[1],不能表示动态行为;而专家系统突出弱点就是知识获取的“瓶颈”问题[2];基于故障树的专家系统诊断系统在一些方面虽得到优化,但是由于故障树模型之间的缺陷,又加上诊断的规则数目较多,当添加修改规则时,易出现规则之间的冲突和冗余,无法保证专家系统高效、正确地运行。
在故障检测与诊断领域中,petri网不仅能够用图形符号表示故障事件系统逻辑关系,知识的完成和诊断推理,而且能够表示系统的动态行为,故petri网模型能够用于机车故障检测和可靠性的分析。
自1962年由carl adam petri提出petri网的概念以来,petri网己广1泛应用于计算机操作系统、通信协议、分布式数据库系统及任务规划和性能评价等领域。在此利用petri网的可达性和状态方程方法,分析故障树信息,解决故障检测和故障传播问题。与基于故障树的诊断方法相比,本文提出的方法具有结构表达图形化、 推理搜索的快速化以及诊断过程的数学化等优点。
2 petri网理论基础及分析
2.1 petri网结构和分析方法
从图形上看,petri网由4种不同类型的元素组成,即库所(place,用“○”表示)、转移(transition,用“|”表示)、连接库所和转移的有向弧及位于库所中的托肯(token,用“·”表示)。库所表示系统状态的逻辑描述,转移表示系统中事件或行为产生过程,输入函数(i)和输出函数(o)分别描述库所和转移之间的联结函数关系。若一库所被赋与k个标记(k为非负整数),则说该库所有k个托肯,也称该库所被标记。于是定义标记petri网为一5元组:
∑=(p,t,i,o,m)。以图1所示petri网为例对上述定义进行具体描述[6]。
∑=(p,t,i,o,m);
p={p1,p2,p3,p4};
m=(1 0 0 0);
i(t1)={p1};o(t1)={p2};
i(t2)={p1};o(t2)={p3};
i(t3)={p2,p3};o(t3)={p4};

图1 petri网模型
petri网的执行过程受控于网中托肯的数量和分布情况,并通过转移的点火得以实现。一个转移可点火,首先该转移必须允许点火,即转移使能。一个转移使能的前提条件是该转移的每一个输入库所中被标记的托肯数至少等于该所到该转移的有向弧数。也就是说一个转移的所有输入库所中至少包括一个托肯(假设每条有向弧的权均为1)。体现petri网动态行为的启动规则是:若库所代表的条件满足,转移就点火,点火后转移的输入库所的托肯数等于原托肯数减去该库所到转移的输出弧数。转移的点火使petri网的标记由m转变为m’。
关联矩阵和状态方程是petri网分析和建模的主要工具,状态方程的表示为
m=m0+ct*uo
m,m0分别点火前后的初始标识集和结果标识集;ct为关联矩阵,u为点火序列,由0,1组成的n×1列矩阵。
2.2 故障树到petri网的转换
故障树是事件间的一种布尔逻辑关系模型,也是一种特殊的树状逻辑因果关系图,它用规定的事件,逻辑门和其它符号描述系统中各种事件之间的因果关系[3][4]。
petri网能够用图形符号表示事件的原因和结果间的关系。按照使能规则每个逻辑门都能够用petri网模型来表示。将故障树的各种逻辑连接关系简化为只有库所和转移组成,以有向弧为连接边的网络,使系统的故障模型简洁、易懂,使故障的传播关系一目了然,更重要的是可以采用petri网的可达性和状态方程来进行故障诊断.根据所建立的诊断petri网模型,就可以通过矩阵操作来诊断故障元件。
2.3 故障petri网诊断方法
在基于故障petri网的故障诊断处理时,其目的主要是找出故障源。输入库所的初始标识可表示为故障发生的征兆,若有征兆出现,则该输入库所就包含一个托肯,否则库所为空。而最终标识的求解可以通过故障petri网可达性和状态方程来实现,推理过程结束时,如果目标库所中含有托肯,则表示故障事件发生了,否则表示没有故障发生。
而由故障传播的特性可知,故障petri网中流动的是故障信息,变迁点火后其输入库所中托肯数目并不发生变化,只是在变迁的输出库所中产生一个新的托肯。在这种情况下,在故障petri网中,在此为了简化建模计算,假设当某个变迁点火后其输入库所中托肯消失,但可从m0…mk-1可知当前状态前各级库所中的托肯。
petri网故障诊断模型的建立:
步骤1:根据诊断问题的逻辑关系,如故障树,建立诊断问题的petri网模型;
步骤2: 写出对应故障征兆和目标故障的初始库所和目标库所;
步骤3: 确定故障petri网的初始标识m0,并求出关联矩阵ct,时间标签计数器k=0;
步骤4:由当前的标示mk根据变迁使能规则,求出变迁点火序列uk,若有uk存在,则转入步骤5,否则步骤6;
步骤5:求系统下一状态,k=k+1;转步骤4;
步骤 6:取最后的标识为系统结果状态,从该标识判断目标库所包含的托肯数,若为1,则该故障事件发生,反之则不然。
3 基于petri网的机车故障诊断模型
现以ss7型电力机车电源柜故障为例[5],其故障树模型如图2所示。
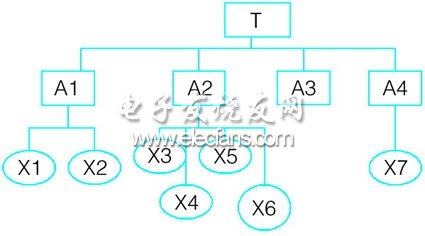
图2 故障树模型
t: 电源柜故障;a1:晶闸管故障;a2:阻容保护板故障;a3:稳压触发板损坏;a4:机破;x1:变压器绕组太小且匝数太多;x2:过电压吸收电阻开路;x3:电容炸裂;x4:b组脉冲变压器接线错误;x5:kbr与kbc接线错误;x6:吸收电阻烧毁;x7:qs34没有接通;
针对图2的故障树建立相应的petri 网模型如图3所示。
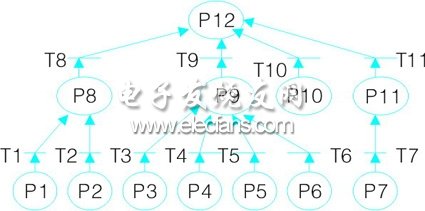
图3 petri网模型
根据图3知源库所为{p1,p2,p3,p4,p5,p6,p7},目标库所为{p12};假定征兆 “吸收电阻烧毁”出现即p6中含有托肯,于是
m0=(0,0,0,0,0,1,0,0,0,0,0,0)则关联矩阵

t6可点火,于是uo=(0 0 0 0 0 1 0 0 0 0 0)t,有状态方程知下一状态:m1=m0+ct*uo=(0 0 0 0 0 0 0 0 1 0 0 0)t,可知托肯从p6转移到p9,根据petri网模型知如果t9可以点火, 库所中的托肯又可以继续转入下一状态,于是得到 u1=「0 0 0 0 0 0 0 0 1 0 0 」t,m2=m1+ct*u1=「0 0 0 0 0 0 0 0 0 0 0 1」t,在此没有下一级转移使能,m2为系统的最终状态:p12=1即电源柜故障发生。
4 结束语
本文对petri网在机车故障诊断领域的应用研究做了新的探索。在分析机车故障的基本特性的基础上,建立故障树模型,结合petri网建模理论,提出了一种适合故障特性的故障petri网模型,该模型能够很好地描述故障的演变和传播特点,解决故障的各种传播模式问题;并提出了故障petri网的诊断方法,该方法可以方便快速地找出故障的传播路径,并应用实际的例子证明了该方法的可行性。
-
LabVIEW在齿轮箱故障诊断中的应用2023-12-25 4025
-
【转】电力电子电路故障诊断方法2018-03-06 4643
-
知识转移策略的跨域故障诊断方法是什么2021-07-12 960
-
异步电机定子故障诊断的仿真与研究2021-09-06 1695
-
基于粗糙集的Petri网故障诊断模型研究2009-12-12 715
-
抽水蓄能机组故障诊断的Petri网方法2009-12-23 1142
-
基于嵌入式Linux的机车故障诊断系统研究设计2010-01-25 761
-
基于Petri网的配电网故障诊断方法2011-05-27 829
-
电网故障诊断方法研究综述2011-06-30 472
-
校园网故障诊断的研究与实现2011-12-27 1002
-
基于模糊Petri网的GIS故障诊断与可靠性分析2017-01-05 785
-
H桥逆变器IGBT开路故障诊断方法研究2017-01-07 1221
-
配电网故障诊断的多因素分级Petri网模型2018-01-08 991
-
Petri网故障诊断方法2018-03-14 1497
-
改进模糊Petri网故障诊断模型2018-03-19 1021
全部0条评论

快来发表一下你的评论吧 !

