

反馈控制系统的特点 如何利用反馈系统产生自激振荡?
电子说
描述
一、引言
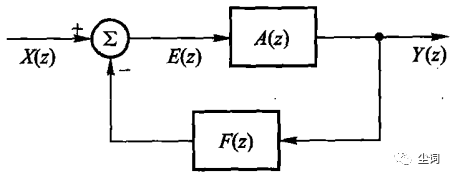

二、反馈系统的基本特性及其应用
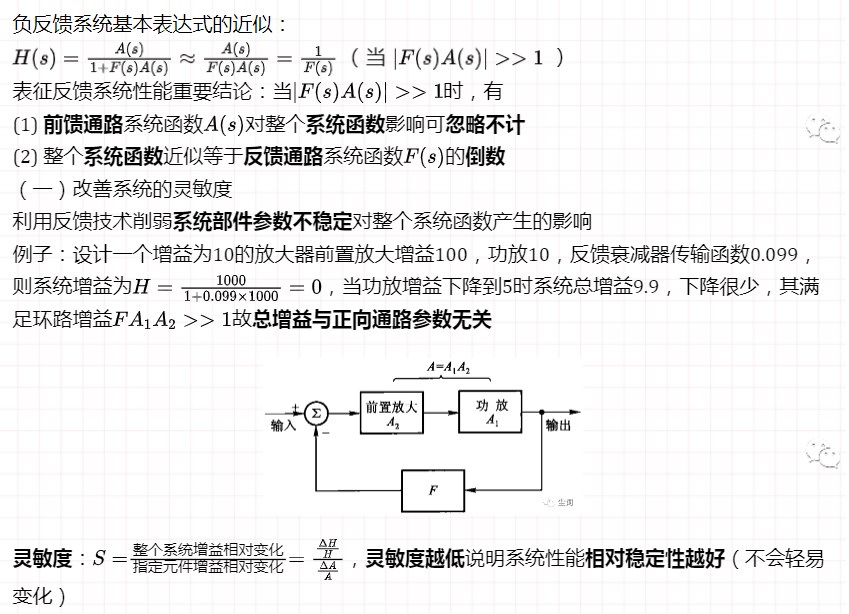
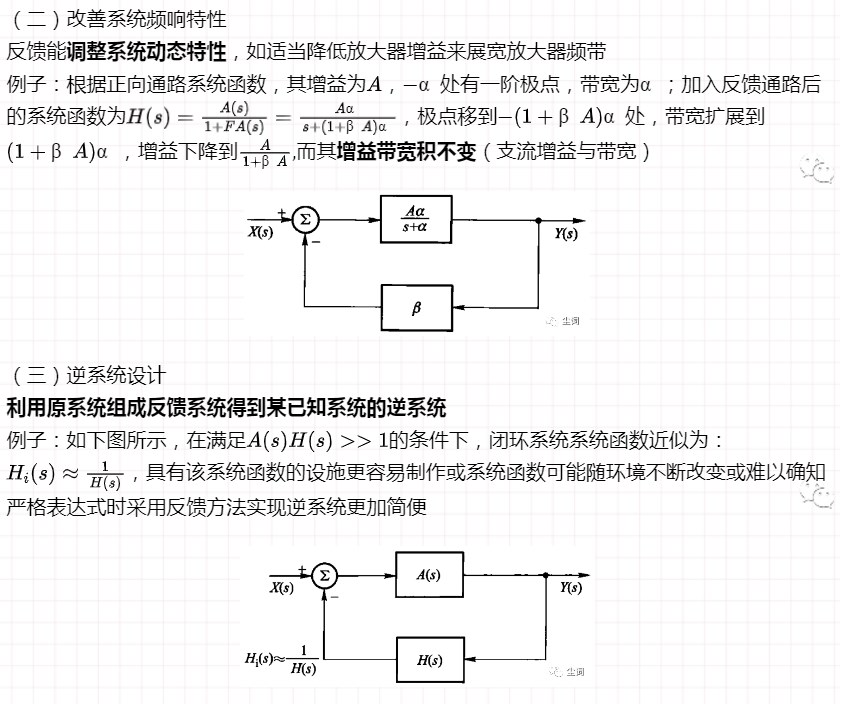
(四)使不稳定系统成为稳定系统
例如移动极点使系统变得稳定,应用如PID、火箭轨道控制和生物繁殖的节制等
三、利用反馈系统产生自激振荡
自激振荡电路反馈系统本质: 正反馈 ,工作于 临界稳定状态 , 极点位于单位圆上 ,一般采用工作于非线性状态下的电子器件。
四、根轨迹
根轨迹法:考察闭环系统函数式中某参量变动时特征方程的极点在s平面内移动的轨迹
(一)根轨迹的模量条件和辐角条件
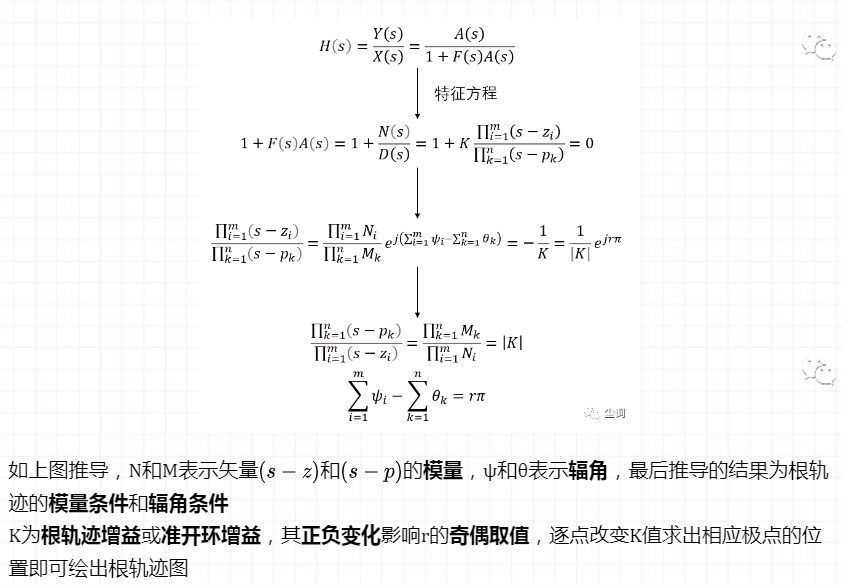

五、奈奎斯特(Nyquist)稳定性判据

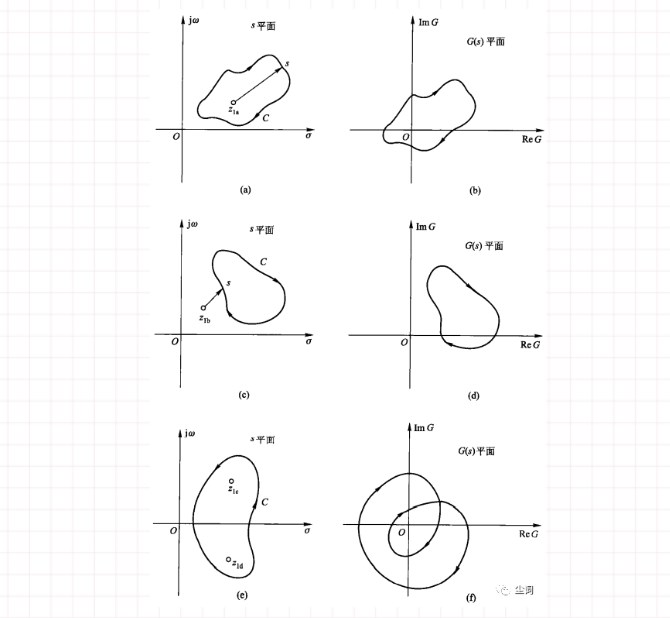
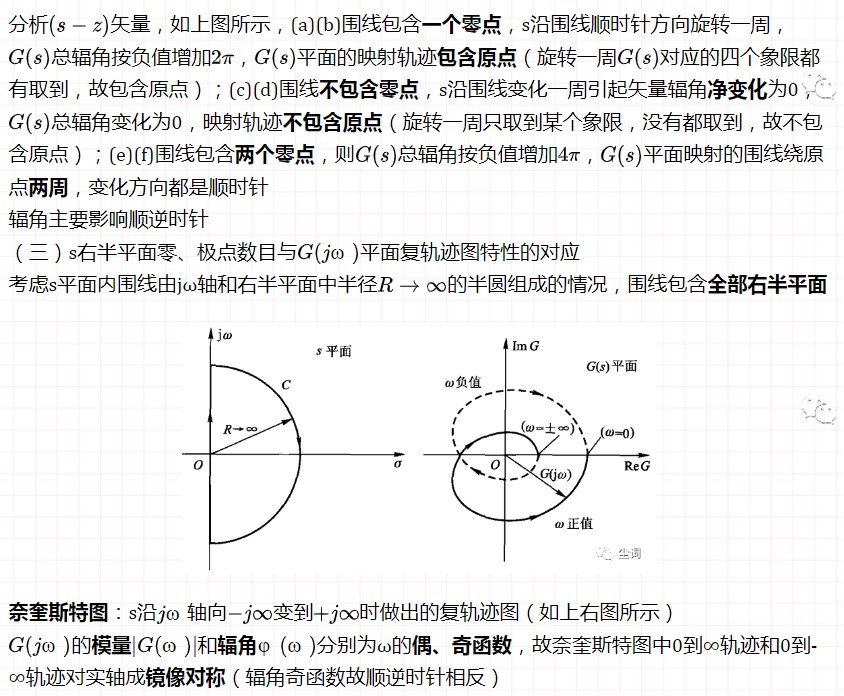

六、信号流图


七、总结
本章主要介绍反馈系统,反馈系统在各个领域都有着非常大的作用。反馈系统主要分为前向通路和反向通路两部分。灵敏度是系统的一大指标,灵敏度越低说明系统性能相对稳定性越好。通过反馈的方式可以很好地调整系统的 稳定性 。反馈同样也能够调整系统的 动态特性 ,用反馈的方式能使 不稳定系统成为稳定系统 。
以上主要用的是 负反馈特性 ,正反馈同样也大有用处。采用正反馈使产生自激振荡。
上述采用反馈运用于系统的数学原理, 本质都是利用系统函数极点在s左半平面系统稳定、在s右半平面系统不稳定的性质 。不稳定系统加上负反馈变成稳定,从系统函数来看本质就是使系统函数没有右半平面的极点;自激振荡采用正反馈则是使极点位于s平面虚轴上(离散就是单位圆上),这样使系统工作与临界稳定状态,就能产生振荡。
介绍的根轨迹判定和奈奎斯特稳定性判据能够判断系统稳定性,奈奎斯特更进一步无需求出极点精确位置,可以用实验测量数据进行分析,更加方便实用。 所有s平面的稳定性判据都是依据极点在s平面右半平面则系统不稳定来进行的 。
本章最后提出了信号流图的基本概念,能很好地简化分析。用梅森公式求解出流图输入输出间的转移函数。信号流图与梅森公式相当于 抓住了研究对象的主要矛盾,借助流图一目了然看清系统内部主体结构和关键参数 。
-
自激振荡原因及条件分析2024-10-06 12228
-
自激振荡是正反馈还是负反馈2024-09-13 2304
-
负反馈自激振荡的条件是什么2024-09-11 4060
-
什么是自激振荡器?它有哪些特点?2024-09-03 5199
-
正反馈和负反馈对控制系统的影响2024-07-30 5803
-
负反馈放大电路产生自激振荡的条件是什么2024-07-09 4392
-
前馈控制系统与反馈控制系统的区别2024-06-17 8018
-
反馈系统中负载效应的计算方法2023-12-01 2683
-
如何设计出面向电机控制优化的反馈系统2023-11-29 396
-
反馈系统分类及并联串联2019-06-24 9987
-
负反馈系统的优点2019-04-16 6323
-
《Feedback Systems》——针对反馈系统设计实用资料.pdf2018-04-18 1929
-
负反馈放大电路自激振荡产生原因及消除方法探讨2012-10-16 6428
-
反馈系统自激振荡2008-09-24 3747
全部0条评论

快来发表一下你的评论吧 !

