基于pid控制方法的操控遥控飞机实例

做控制时，大家经常会有这样的感受“代码很丰满，现实很骨感”，这是因为将计算机指令转移到实际硬件时，由于物体的惯性以及各种非理想化的因素影响，往往会出现实际与预期不符合的情况。

这篇文章将以“操控遥控飞机从地面飞到10米高度并悬停”为例子，用最通俗易懂的方式，让你理解PID。在这个问题中，我们假设加速度是可以直接调控的（实际生活中往往也是这样），因此，我们输入的量为加速度的大小和方向（正负），而我们最终想要得到的结果就是高度稳定在10米。

首先我们来讲控制方法：

控制方法主要分为“开环控制”和“闭环控制”，这两种控制方法的简单理解为：

开环控制：计算出飞机从地面到10米高度所需要的加速度以及作用时间，然后将其编写为一条固定的指令，“一次执行，全过程受益”。

闭环控制：在飞机飞行的过程中，系统时刻关注飞机的状态，并做出相应的调整。而PID控制就是最常用的闭环控制。

PID原理

一讲到原理，很多人都会搬出PID公式，数学较好或者学过自控的人还好，要是遇见一个半路转行做控制的，看见“微分”和“积分”，头都大了。其实，由于生活中信号采样具有一定的间隔，因此我们经常遇见的都是离散信号的控制，只需要读懂下图即可：

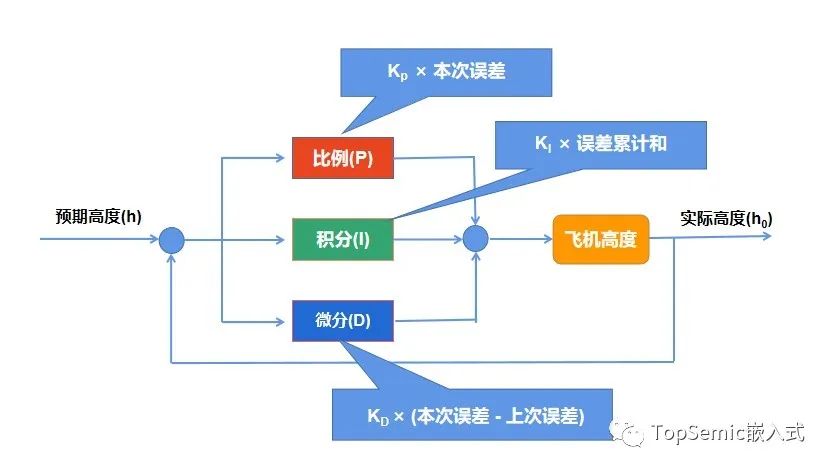
实践出真知(python实现PID)

3.1 导入包

 

`import time`

`import matplotlib.pyplot as plt`

 

3.2 PID实现

 

# 实现一个PID控制器
class PIDController:

    def __init__(self, kp, ki, kd):

        """

        初始化PID控制器

        参数:

        kp (float): 比例系数

        ki (float): 积分系数

        kd (float): 微分系数

        """

        self.kp = kp  # 比例系数

        self.ki = ki  # 积分系数

        self.kd = kd  # 微分系数

        self.prev_error = 0  # 上一次的误差

        self.integral = 0  # 误差积分值

    def calculate(self, setpoint, current_value):

        """

        计算PID控制器的输出

        参数:

        setpoint (float): 设定值（目标值）

        current_value (float): 当前值（被控制的系统当前状态）

        返回:

        output (float): 控制器的输出

        """

        error = setpoint - current_value  # 计算误差

        self.integral += error  # 更新误差积分

        derivative = error - self.prev_error  # 计算误差导数

        output = self.kp * error + self.ki * self.integral + self.kd * derivative

        # 计算控制输出，包括比例、积分和微分部分

        self.prev_error = error  # 保存当前误差作为下一步的上一次误差

        return output  # 返回控制器的输出

 

3.3 飞行器模拟

 

#飞行器模拟
class AircraftSimulator:

    def __init__(self):

        self.height = 0  # 飞行器初始高度为0

        self.velocity = 0  # 飞行器初始速度为0

    def update(self, throttle, time_step):

        """

        更新飞行器状态：高度和速度

        参数:

        throttle (float): 油门输入，控制引擎输出的力量

        time_step (float): 时间步长，模拟器更新的时间间隔

        """

        acceleration = throttle - 0.1 * self.velocity  

        # 根据简化的动力模型计算飞行器的加速度

        # 加速度等于油门输入减去速度的一部分，这是简化的模型

        self.velocity += acceleration * time_step  

        # 根据加速度更新速度

        # 新速度等于当前速度加上加速度乘以时间步长

        self.height += self.velocity * time_step  

        # 根据速度更新飞行器的高度

        # 新高度等于当前高度加上速度乘以时间步长

 

3.4 主函数与绘图

 

# 主函数

def main():

    # PID参数

    kp = 5.0

    ki = 0.1

    kd = 10

    # 初始化PID控制器和飞行器模拟

    pid_controller = PIDController(kp, ki, kd)

    aircraft_simulator = AircraftSimulator()

    target_height = 10.0

    time_step = 0.1

    total_time = 20  # 总模拟时间增加到20秒

    current_time = 0.0

    # 存储时间和高度数据的列表

    time_data = []

    height_data = []

    # 模拟循环

    while current_time < total_time:

        # 使用PID控制器计算控制信号

        control_signal = pid_controller.calculate(target_height, aircraft_simulator.height)

        # 添加扰动

        disturbance = -1.5

        control_signal += disturbance

        # 使用控制信号和时间步长更新飞行器模拟

        aircraft_simulator.update(control_signal, time_step)

        # 存储时间和高度数据

        time_data.append(current_time)

        height_data.append(aircraft_simulator.height)

        current_time += time_step

        time.sleep(time_step)  # 添加时间延迟以模拟实时行为

    print("Simulation completed.")

    # 绘图

    plt.plot(time_data, height_data, label='Height')

    plt.axhline(y=target_height, color='r', linestyle='--', label='Target Height')

    plt.xlabel('Time (s)')

    plt.ylabel('Height (m)')

    plt.title('Aircraft Height Control with Random Disturbance')

    plt.legend()

    plt.grid(True)

    plt.show()

if __name__ == "__main__":

    main()

 

实验与参数理解

PID的控制经常会涉及到KP、KI、KD三个参数的调节，如果盲目调节则会花较长时间，接下来我们将用直观实验来理解以下几个参数的具体含义。

4.1 比例环节

计算公式为KP × 误差，具体的含义即为误差越大，值越大。这一点是非常直观的，误差越大则说明偏离预期值越远，我们要加大“油门”，快速调整！以下是当KI、KD为0，只有KP=5的测试结果：

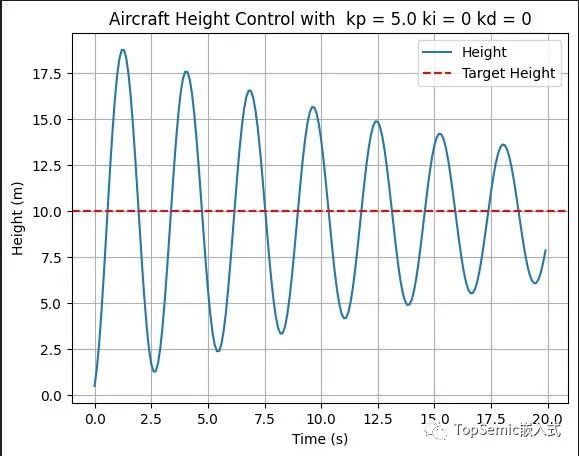
从图中我们可以看到虽然慢慢的想10收敛，但由于误差越大，其“油门”越大，就像是一个“莽夫”，尽管每次都在调整，但总是用力过猛！

4.2 微分环节

计算公式为KD × (本次误差 - 上次误差)，对于这个公式，我们可以理解为用来中和“用力过猛”。以下是当KP=5、KD=10、KI=0的测试结果：

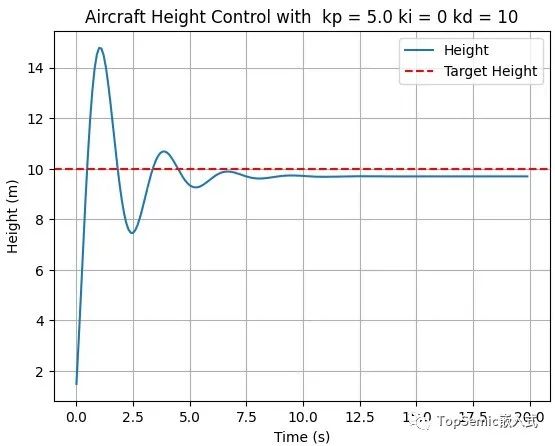
显然，这个结果要比上次好很多，但始终低于10，这是因为我们在模拟中加入了一个干扰条件：

 

# 添加扰动

        disturbance = -1.5

        control_signal += disturbance

 

因此，要想消除这个干扰，就需要积分环节的加入。

4.3 积分环节

积分环节的公式为KI × 误差累计和，用官方的语言来说，用来调整“稳态误差”，其实，所谓的稳态误差就可以理解为“一直存在的误差”，也就是在本次实验中加入的持续干扰！以下是当KP=5、KD=10、KI=0.1的测试结果：

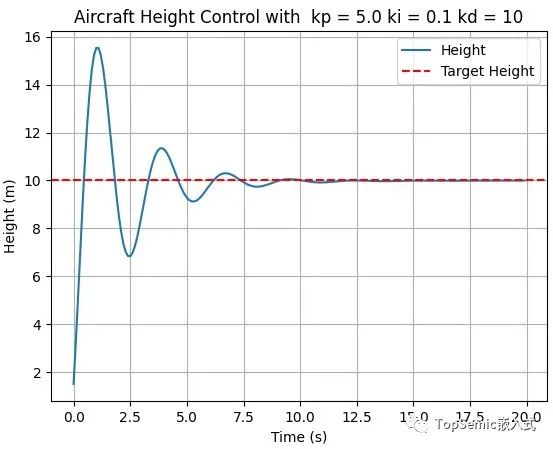
从这次的测试中，我们看出，得到了几乎完美的结果！

总结

对于PID参数调节，认准3个点：

P:大力出奇迹

I：消除持续存在的误差

D：“中和”用力过猛，减少波动

        责任编辑：彭菁