最少需要几个加法器IP才可以实现累加器的功能呢？

已知一个加法器IP，其功能是计算两个数的和，但这个和延迟两个周期才会输出。现在有一串连续的数据输入，每个周期都不间断，试问最少需要例化几个上述的加法器IP，才可以实现累加的功能。

设计分析

实现累加器的加法器例化的个数。按照原文大佬的设计方法，因为数据连续且加法器的延迟周期是2，使用使用一个实现累加，会有一半的数据丢失。那这样设计他就将奇数偶数的数据进行了分开做一级累加，然后第二级将奇数偶数的累加结果再累加。这样做共需消耗3个加法器。

这样设计当然没问题，但是这样设计是否是最少呢？我先抛出我的思考，我认为在允许少量逻辑设计的情况下，最少需要例化两个上述的加法器IP可以实现累加。

如果比较极限的情况下，一个都可以，先把一串数据使用寄存器缓存，然后一个一个取出来慢慢算即可，但这样是不太可取的，首先，数据是连续的并没有给出数据的极限长度，也就是说不论用任何涉及存储结构进行缓存，都没法确保该次数据能完全被存储。如果题目改成一串连续数据输入，长度最大为10，那我认为用寄存器缓存这样的设计是合理的。

设计架构

回到设计思路：用两个加法器的结构如图示。

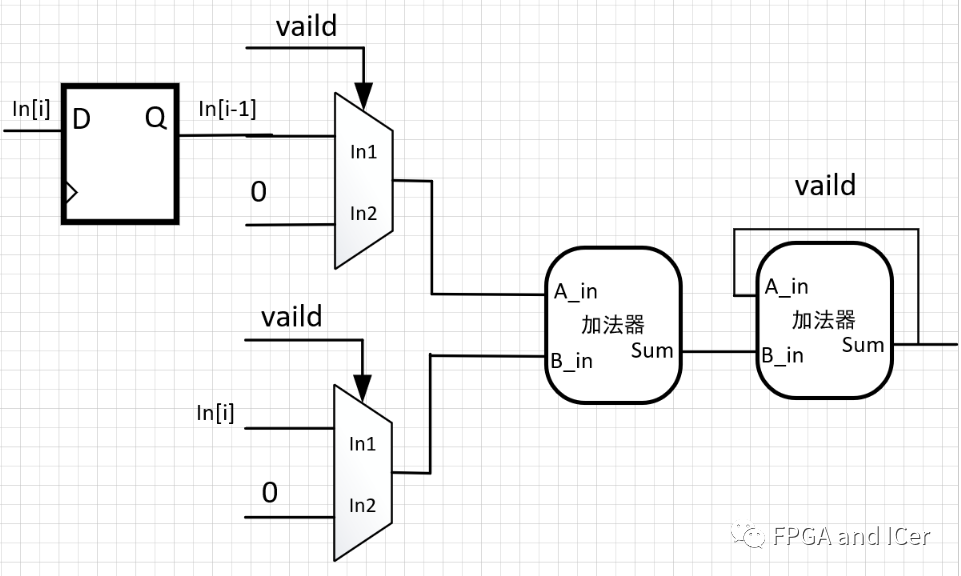
设计实现

加法器设计

假设两个时钟周期延时加法器代码如下，通过例化加法器进行构建累加器。

 

//加法器IP
module adder
#(parameter DATA_WIDTH = 8)(
    input clk,
    input rst_n,
    input [DATA_WIDTH-1:0] a_in,
    input [DATA_WIDTH-1:0] b_in,
    output reg [DATA_WIDTH-1:0] out
  );
  reg [DATA_WIDTH-1:0] sum;
  always @(posedge clk or negedge rst_n)begin
    if(rst_n == 'd0)begin
      sum <= 'd0;
      out <= 'd0;
    end
    else begin
      sum <= a_in + b_in;
      out <= sum;
    end
  end
endmodule

 

累加器设计

 

//累加器实现
module adder_for_acc
  #(parameter DATA_WIDTH = 8)
   (
     input                        clk,
     input                      rst_n,
     input       [DATA_WIDTH-1:0] din,
     input                  din_valid,
     output reg            dout_valid,
     output reg [DATA_WIDTH-1:0] dout
   );

  reg [DATA_WIDTH-1:0]din_r0;

  //打一拍
  always @(posedge clk or negedge rst_n)begin
    if(rst_n == 'd0)begin
      din_r0 <= 'd0;
    end
    else if(din_valid==1'B1)begin
      din_r0<= din;
    end
    else begin
      din_r0<='d0;
    end
  end

  //adder0_valid信号
  reg adder0_valid;
  always @(posedge clk or negedge rst_n)begin
    if(rst_n == 'd0)begin
      adder0_valid <= 'd0;
    end
    else if(din_valid==1'B1)begin
      adder0_valid<=!adder0_valid;
    end
    else begin
      adder0_valid<='d0;
    end
  end

  wire[DATA_WIDTH-1:0] a_in = (adder0_valid && din_valid)?din:0;
  wire[DATA_WIDTH-1:0] b_in = (adder0_valid)?din_r0:0;
  wire[DATA_WIDTH-1:0] ab_sum;

  adder adder0_dut (
    .clk  (clk   ),
    .rst_n(rst_n ),
    .a_in (a_in  ),
    .b_in (b_in  ),
    .out  (ab_sum)
  );
  //第一级加法器输出有效信号
  reg [1:0]adder0_valid_dly;
  wire ab_sum_valid = adder0_valid_dly[1];
  always @(posedge clk ) begin
      adder0_valid_dly<={adder0_valid_dly[0],adder0_valid};
  end

  wire [DATA_WIDTH-1:0] sum_in;
  wire [DATA_WIDTH-1:0] ab_sum_in = (ab_sum_valid)?ab_sum:0;
  wire [DATA_WIDTH-1:0] accsum_in = (ab_sum_valid)?sum_in:dout;

  adder adder1_dut (
    .clk  (clk      ),
    .rst_n(rst_n    ),
    .a_in (ab_sum_in),
    .b_in (accsum_in),
    .out  (sum_in   )
  );
  
  //第二级加法器输出有效信号
  reg [3:0]din_valid_r0;
  reg [1:0]adder1_valid_dly;
  wire adder1_outvld = adder1_valid_dly[1];
  always @(posedge clk ) begin
    adder1_valid_dly<={adder1_valid_dly[0],ab_sum_valid};
  end
  //输出
  always @(posedge clk ) begin
    din_valid_r0<={din_valid_r0[2:0],(din_valid || adder0_valid)};
  end
  always @(posedge clk or negedge rst_n) begin
    if(rst_n == 'd0)begin
      dout <= 'd0;
      dout_valid <= 'd0;
    end
    else if(adder1_outvld == 1 && (din_valid_r0[3]==1 && din_valid_r0[2]==0))begin
      dout <= sum_in ;
      dout_valid <= 'd1;
    end
    else begin
      dout <= dout ;
      dout_valid <= 'd0;
    end
  end

endmodule

 

代码架构设计

打拍：先对数据用寄存器缓存一拍，输入数据暂时用in[i]表示，缓存。

第一级加法器输入选择valid：因为前级积累一拍的数据，设计valid用于指示加法器的输入数据。

第一级加法器信号输入：根据valid信号进行选择数据输入。

调用第一级加法器，同时对输入valid信号进行打两拍处理，指示有效的输出数据。

第二级加法器信号输入：根据valid信号进行选择数据输入。

调用第二级加法器，同时对输入valid信号进行打两拍处理，指示有效的输出数据。

输出结果和valid信号。

经过分析，目前设计延时是4拍，也即两级，这里dout和valid使用的是时序逻辑输出，所以在输入valid拉低后的第五个时钟周期输出正确的结果。

仿真测试

设计仿真测试代码对代码进行测试，这里使用了递增数测试代码可用性，在实际测试时，可通过改变DATA_LEN的大小测试单次递增累加后的结果，后续结果依次递增为第一次的N倍。

 

`timescale 1ns/1ps
module adder_for_acc_tb;

  // Parameters
  localparam  DATA_WIDTH = 8;
  localparam  DATA_LEN = 5;
  // Ports
  reg clk = 1;
  reg rst_n = 0;
  reg [DATA_WIDTH-1:0] din;
  reg din_valid = 0;
  wire  dout_valid;
  wire [DATA_WIDTH-1:0] dout;

  adder_for_acc 
  #(
    .DATA_WIDTH (
        DATA_WIDTH )
  )
  adder_for_acc_dut (
    .clk (clk ),
    .rst_n (rst_n ),
    .din (din ),
    .din_valid (din_valid ),
    .dout_valid (dout_valid ),
    .dout  ( dout)
  );
  always @(posedge clk or negedge rst_n)begin
    if(rst_n == 'd0)begin
            din <= 'd0;
      din_valid <= 'd0;
    end
    else if(dout_valid == 1)begin
      din <= 'd0;
      din_valid <= 'd1;
    end
    else if(din == DATA_LEN)begin
      din <= din;
      din_valid <= 'd0;
    end
    else if(din != DATA_LEN)begin
      din <= din + 1;
      din_valid <= 'd1;
    end
    else begin
      din <= din;
      din_valid <= 'd0;
    end
  end

  always #5  clk = ! clk ;
  initial begin
    begin
      #100;
      rst_n = 1;
      #1000;
      $finish;
    end
  end

 
endmodule

 

仿真截图

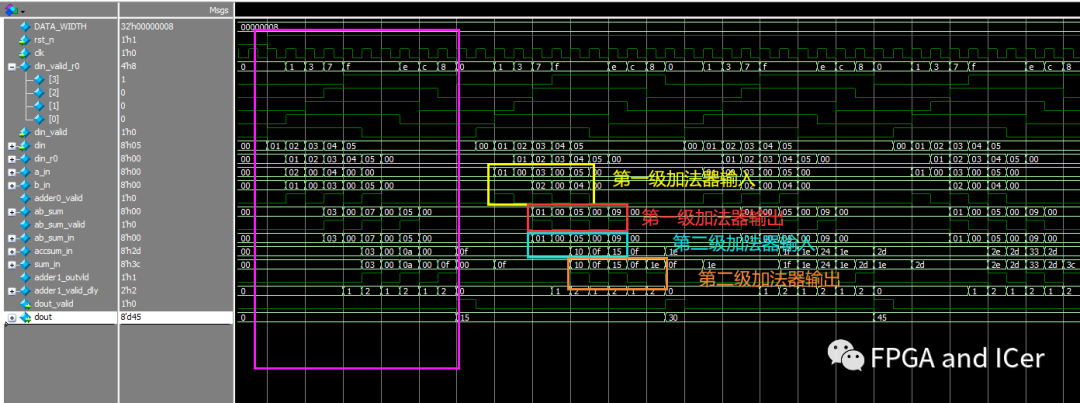
仿真分析

在图示仿真可知，累加器功能正常，在din_valid信号拉低后第五拍可得到输出结果，功能正常。

审核编辑：刘清