自发辐射的机制是什么？为什么会自发辐射？

作者：刘伟涛 吴蜀明  

－作者简介－

Peter W. Milonni

罗切斯特大学物理和天文学系教授

－译者简介－

刘伟涛，理论物理研究所2017级博士生

导师：邹冰松研究员

研究方向：强场原子核物理理论

吴蜀明，理论物理研究所2019级博士生

导师：邹冰松研究员

研究方向：强子物理

译者注

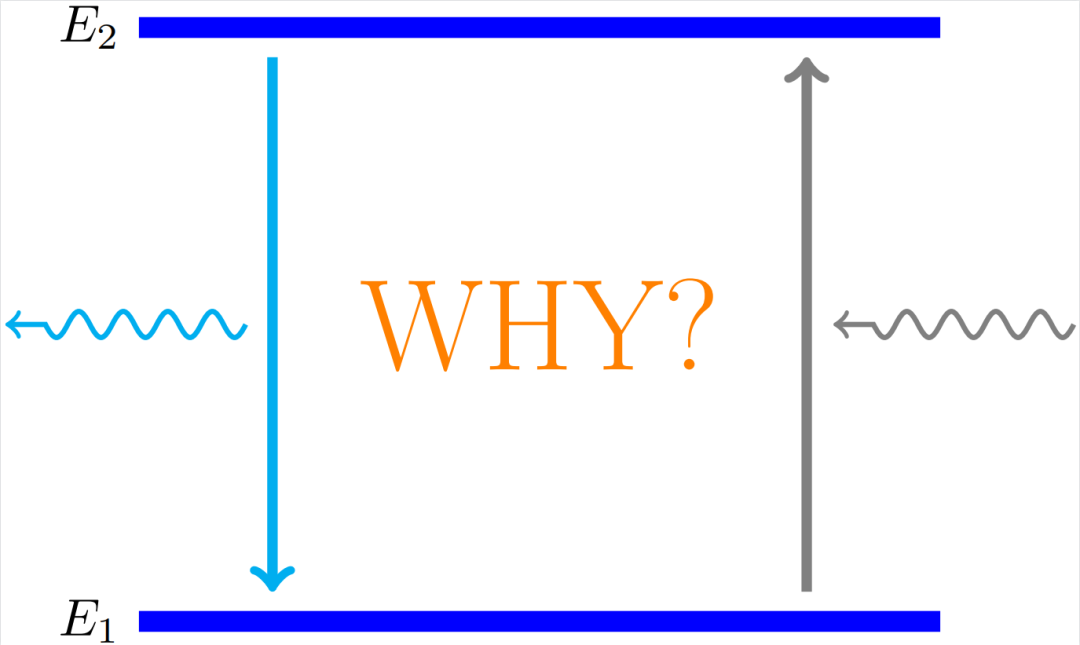
在常温下，我们经常可以看到自发辐射，却难以观察到自发吸收，这是为什么呢？Milonni的这篇文章，从半经典的角度解释了自发辐射的机制，或许可以给我们一些启示。

这篇文章讨论了一个长期存在的问题——为什么一个被激发的原子可以产生辐射？当我们把辐射反应和辐射场的零点涨落联系起来，我们得到了一个令人满意的图像。我们强调，涨落-耗散定理联系了这两个效应。 

啊，只一闪耀，热炽的原子就在寒冷的寂灭里融消。

——P. B. Shelley, Adonais

01.

问 题

Feynman 教授曾经讲过这样一个故事[1]：

你可能会猜测这个问题从何而来，事实上它出自我的父亲。在我去过麻省理工、去过普林斯顿之后，我回到了家里，我的父亲说：“你现在接受了科学教育。而我一直想了解一些我理解不了的问题。所以，儿子，我希望你能给我解释。”我说：“好的。”

他说：“我理解他们所说的光是从原子里面发射出来的，这时原子从一个激发态跃迁到了一个低能态。"

我说：“是这样的。"

“而光是一种粒子，我想他们把它称作光子。”

“是的。”

“所以如果光子是激发态的原子到低能态时发射出来的，那光子就必然在激发态的原子里。”

我说：“不。”

他说：“那么，你怎么看这个问题，一个光子跑了出来，但这个光子却不在原先的激发态里？”

我思考了几分钟，然后说：“我很抱歉，我不知道。我没办法给你解释。”

他很失望，在那么多年中，他都尝试教给我一些东西，但结果却是很失败。

直到今天，为什么一个原子会辐射，或者一个原子怎样辐射，这个问题都会引起大多数物理学家相似的回答。但是过去的十多年中我们取得了一些进展。在这篇文章中，我将尽我所能地用最简单的方式阐释最近的发展。为了更好地了解这个问题的来龙去脉，我将在第2节强调不同辐射现象的关联性，而在第3节来讲一些相关的历史。我用第4节和第5节来讲两个可能的自发辐射的诠释，而在第6节，我在某种程度上把它们结合成一种诠释。在第7节我会以一些细节的讨论来结束这篇文章。

02.

关联性

我们身边绝大多数光，都来源于自发辐射。可以说，没有自发辐射，我们人类就不能生存。

我们考虑一个辐射热源。这样一个热源中，一个原子同时存在自发和受激两种辐射方式。这两种辐射的速率分别为  和  ，这里的  和  分别是自发辐射和受激辐射的Einstein系数，而  是Planck能谱密度。对于一个给定的Bohr频率，因为  [2]，这两个速率的比值是

如果我们把太阳看成一个  的热源，对于  ，这个比值大约为400，而对于  ，这个比值大约为30。这样，当我们把太阳当作一个理想的黑体辐射源时，它绝大多数的可见光都来源于自发辐射。

自发辐射其实是非常普遍的，以至于我们用了很多名词来指代这样一件相同的事情。如果一个原子（也可以是分子）不是被热激发的，而是由其他方式激发的，自发辐射又被称为发光。萤火虫就是发光的。而对于发光，又有不同的名称，这又具体地取决于这些激发态是怎样产生的（比如电发光、化学发光等）。如果激发是因为吸收了辐射，那么自发辐射又被称作荧光。有时，一些分子会处在亚稳态，这样在辐射场关闭后，这些分子仍然可以产生自发辐射。这种现象，人们称作磷光。在黑暗中，一些雕像会神奇地发光，这就是磷光。

当然，激光的产生是因为受激辐射。然而，当激光器打开时，产生激发效应的光子实际上也是来源于自发辐射。

03.

历 史

1887年，Hertz的实验证实了振荡的电荷是会辐射的。在Lorentz的光和物质的理论[3]中，原子的辐射被归咎于原子中电子的振荡。但这并不能让我们理解为什么它们的辐射总有一些特定的频率。而原子的吸收和发射频率被生硬地塞进一个包含了“弹簧系数”的电子结合理论。但这一切在1913年被Bohr提出氢原子理论所改变了。

Bohr认为自发发射是非经典的，而“自发”意味着非因果性。即我们不能准确地预知一个被激发的原子什么时候会完成一个量子跃迁，然后发射一个光子。

Einstein在1917年进一步揭示了自发辐射的非经典性质。Einstein工作中的特别之处在于他推测在自发辐射中，原子必然会有一个反冲。这个反冲在经典理论中不能得到解释，因为在经典理论中，一个原子辐射出的场不会有一个线性的动量[4]。根据Einstein的观点，“放出的辐射不会出现球面波”[5]，如果原子辐射出球面波，那么它就不会有反冲。利用热力学的论点，Einstein推导了自发辐射和受激辐射的系数比值  。

第一个从第一性原理的角度推导系数  的人是Dirac[6]，他使用了一套新的量子辐射理论。而在经典的电磁学中，没有人能够建立一套令人满意的自发辐射理论[7]。要解释从萤火虫发光到激光器启动的这一系列的问题，需要量子电动力学。

但是，量子电动力学又对自发辐射现象提供了一个怎样的物理图像呢？在大量相关的文献中，可以找到两种答案。

较早的答案将自发辐射和经典理论中被熟知的辐射反应联系起来。Dirac曾在文章中写道“既然现有的理论给出了自发辐射的解释，那么它也能够给出辐射体系的辐射反应”[6]。这样的解释，根据同一年Landau发表的一片文章[8]和更早一些的van Vleck发表的使用到对应原理的文章[9]，也是无可指摘的。

一段时间之后出现了另外一种答案。对于Lamb位移的研究使得人们有了一个新观点：Lamb位移的能级移动——和自发辐射所产生的“自然展宽”一样——都可归因于电磁场在零点的量子涨落。在1948年的一篇著名的文章中，Welton[10]认为自发辐射“可以被认为是由涨落的场而导致的强制的辐射”。

人们逐渐意识到这两种观点在本质上是相同的。在讨论它们的等价性之前，我们有必要先更加仔细地分别讨论这两个观点，并认识什么是零点场。

04.

辐射反应

考虑一个振荡的电偶极矩  。我们都知道这个偶极矩辐射能量的速率是

箭头表示我们将若干个周期内的功率求平均值。

假设有一个电荷  ，它相对于一个无穷质量的相反电荷的位置为  。这时我们就有了一个振荡的偶极矩  ，辐射速率由(4.1)给出。因为一个质量为  的振荡电荷的总能量为

我们得到了

此式即为能量  因为辐射而减少的速率。

假设我们希望对原子中的一个电子利用(4.3)。如果电子可以从一个能级  跃迁到另一个能级  ，我们将  认作跃迁频率  ，而

便是高能级的辐射衰变概率。然而，这些推导都是经典的。为了能够给出一个量子力学的预计，我们必须用跃迁谐振子强度给它一个“权重”，即[11]

这里的  是跃迁的偶极矩阵元。

但不幸的是，这只是Einstein自发辐射系数  的一半，我们将在之后继续讨论这个问题。

假设我们计算点电荷振荡时在自身所形成的电场。在一些相当繁琐的计算之后[12]，我们可以得到

这即所谓的辐射反应场。在这个场的作用下，我们所考虑的偶极子能量的变化率

同样，这里的箭头表示若干个周期内取平均值的结果。

(4.3)和(4.7)的结果是一致的。这表明我们可以将振荡电荷能量的散失归因于它的“自场”，即(4.6)。这样，通过经典-量子对应(4.5)，我们发现自发辐射是由原子中电子的辐射反应场引起的，只是我们的衰变速率结果有一个因子为  的偏差。

05.

真空场

由量子力学可知道，一个频率为  的谐振子，它的零点能为  。相似地，由量子力学可知，电磁场的任意模式，都有  的零点能。但是在  的频率范围内，单位体积内存在  个模式[13]。这样在体积为V的空间内，在  的频率区间便存在一个电磁零点能

而  是真空电磁场的“零点谱”。

这个场会对原子产生影响吗？根据Einstein的理论，在能谱密度为  的场中，受激辐射的速率是  ，其中

是受激辐射系数。这样由零点场所导致的偶极矩阵为  ，频率为  的辐射速率为

非常有趣的是，  。

受激辐射和吸收的系数  是相同的（如果我们忽略简并的因素）。那么为什么没有从零点场里的自发吸收呢？

06.

部分的统一

、  都等于Einstein自发辐射系数  的一半绝对不是偶然。作为理解这个问题的第一步，我们将看到辐射反应和零点场共有着一个相当密切的关系。

为了建立这样一种关系，一个方便的做法是先考虑一个“自由的”电子，这个电子受到真空场和自身辐射场的作用。在形式上，海森堡运动方程和经典运动方程是一致的：

这里的  是真空，或者称作零点电场。（实际上它仅仅是这个场在  方向上的分量，因为为了简便，我们只考虑沿  方向的电子运动。）我们把(6.1)写成

而此处

是电子的观测质量，  是“裸”质量，  称作"电磁质量"。

遗憾的是，电磁质量被证明是无穷大的。在我们的非相对性理论中它是线性发散的；在相对性理论中它是对数发散的。我们忽略这个困难并且假设裸质量和电磁质量加起来等于一个常数  。这个过程被称作质量重整化。而当今的物理学便是建立在重整化这一“原则”之上的。

在很长一段时间内，物理学家曾经尝试避免这样的无穷大量。例如Wheeler-Feynman吸收子理论[14]，它会导致一个  的项，但没有电磁质量项。最近，一些观点认为，虽然我们还没有一个相对论性的理论，但在完整量子力学的辐射理论应有  [15]。无论如何，我们需要谨记Dirac对于重整化的异议[16]：“这仅仅是一些不合理的数学。合理的数学只应该忽略小量——而不是忽略一个你不想要的无穷大量！”

我们将会假设(6.2)是正确的。但如果它是正确的，它必须和量子力学的基本观点是兼容的。具体来说，算符方程(6.2)得到的解  ，和相对应的线性动量  的解，必须满足对易关系  。我们可以得到[17]

所以运动方程(6.2)保证了反对易关系。在(6.4)中，  是零点场  的能谱，而我们定义了  。

现在不难看出，(6.4)中分母上的  起源于(6.2)中的辐射反应场对应的项  。进一步看，零点场的能谱密度  正比于  （可参考(5.1)），这样我们在(6.4)中可以消去  的因子，然后剩下

如果  正比于  的其他次幂，我们便不能保证  对易关系！

我们这里讨论的是一个涨落-耗散定理[18]的例子。如果存在一个辐射反应场，则必然存在一个零点场，反之亦然成立。更进一步地，零点场的能谱正比于  的三次方，这是因为辐射场正比于  的三阶导数[17]。这便是辐射场和零点场之间的密切联系，也是等式  成立的原因。

早先对于  和  的“推导”在某种程度上具有启示意义。然而，一个量子力学的计算在很大程度上支持了这样的结果。这样的方式计算明确地揭示了辐射场和零点场对自发辐射的贡献。对于一个处在激发态的原子，这两个贡献加起来便得到总共的辐射速率

即Einstein常数。然而，对于一个基态的原子，这两个贡献却互相抵消，得到衰变速率  。而后者至少从量子力学的角度解释了为什么不存在从零点场的自发吸收[19]。

辐射场和零点场相互作用的关键便是它们之间的涨落-耗散关系。就像电路中Nyquist-Johnson电压涨落和电阻相关，零点场的涨落也和辐射阻力（或者说辐射反应）相关。在这两个例子中，耗散力和与之相对应的涨落力的频谱都有着明确的关系。

和  以因子  区别于Einstein系数A。这个在我们的讨论中是非常重要的因子，在辐射理论中有着很长的历史，特别是在量子理论的胚胎时期。比如，在1913年Einstein和Stern发现如果我们假设偶极振荡的零点能为  ，便可以推导Planck谱密度[4]。从现在的观点看，经典理论不能计入场的零点能，即对频率为  的模式，应有  的能量。这部分能量加上偶极振荡的零点能  ，便给出了总共的零点能  ，这便是Einstein和Stern总结的谐振子的能量[4]。在量子理论中，两种贡献以一种自然的方式出现，而(6.6)给出了一个很好的例子。

07.

细 节

为了预防一些专家的反对意见，我在这里谈谈我的这种观点和早前两种观点的联系。这个新观点同时被来自三个不同的研究所的物理学家“发现”[20,21]。这些研究受到了Ackerhalt等人的工作[22]的启发，而Ackerhalt等人的工作奠定了用辐射反应解释自发辐射的量子力学基础。更加精巧而富有洞察力的观点来自于Fain[23]和Dalibard等人[24]。Sciama[24,25]还使用  和  之间的涨落-耗散关系讨论了黑洞的热力学。

对于自发辐射速率的海森堡绘景的推导涉及到了原子算符和场算符的交换乘积。如果我们使用对称的顺序，我们得到的是  ，即(6.6)。而一个“正常”顺序，会导致  ，而使用其他的顺序还可以得到  等结果。当然，我们所得到的自发辐射系数A的表达式是不变的，这是因为我们重排的算符实际上是对易的，但我们对自发辐射速率的诠释却会发生改变。这又是辐射场与零点真空场的紧密的涨落-耗散关系的结果。Dalibard等人[24]主张在某些情况下，对称次序是更为合理的。

很多物理效应都可归因于零点电磁场。包括van der Waals力和Casimir力[27]。我们会自然地联想，会不会存在其他一些效应可以归因于辐射反应，就像自发辐射一样。答案是存在这些效应[28]。而关于这些效应的理论在本质上和自发辐射并无不同。但据我所知，在之前没有人将van der Waals力或者Casimir力归于辐射反应。如Jaynes[29]所说，我们花费了很长时间才认识到辐射场中涨落-耗散定理的作用。

08.

致 谢

我要感谢David Stoler在不同场和鼓励我来写一篇关于自发辐射的教学文章，也感谢他和我关于光子所展开的有趣的讨论。许多同事帮助我明确了在这个问题上的思路，特别是最近Richard J. Cook. 我还要感谢Alan H. Paxton将文献[1]带给我。

编辑：黄飞