

普林斯顿博士:手写30个主流机器学习算法,全都开源了!
描述
Hello,我是kk~
NumPy 作为 Python 生态中最受欢迎的科学计算包,很多读者已经非常熟悉它了。它为 Python 提供高效率的多维数组计算,并提供了一系列高等数学函数,我们可以快速搭建模型的整个计算流程。毫不负责任地说,NumPy 就是现代深度学习框架的「爸爸」。
尽管目前使用 写模型已经不是主流,但这种方式依然不失为是理解底层架构和深度学习原理的好方法。最近,来自普林斯顿的一位博士后将 NumPy 实现的所有机器学习模型全部开源,并提供了相应的论文和一些实现的测试效果。
-
项目地址:https://github.com/ddbourgin/numpy-ml
根据机器之心的粗略估计,该项目大约有 30 个主要机器学习模型,此外还有 15 个用于预处理和计算的小工具,全部.py 文件数量有 62 个之多。平均每个模型的代码行数在 500 行以上,在神经网络模型的 layer.py 文件中,代码行数接近 4000。
这,应该是目前用 NumPy 手写机器学习模型的「最高境界」吧。
谁用 NumPy 手推了一大波 ML 模型
通过项目的代码目录,我们能发现,作者基本上把主流模型都实现了一遍,这个工作量简直惊为天人。我们发现作者 David Bourgin 也是一位大神,他于 2018 年获得加州大学伯克利分校计算认知科学博士学位,随后在普林斯顿大学从事博士后研究。
尽管毕业不久,David 在顶级期刊与计算机会议上都发表了一些优秀论文。在最近结束的 ICML 2019 中,其关于认知模型先验的研究就被接收为少有的 Oral 论文。
David Bourgin 小哥哥就是用 NumPy 手写 ML 模型、手推反向传播的大神。这么多的工作量,当然还是需要很多参考资源的,David 会理解这些资源或实现,并以一种更易读的方式写出来。
正如 reddit 读者所质疑的:在 autograd repo 中已经有很多这样的例子,为什么你还要做这个项目?
作者表示,他的确从 autograd repo 学到了很多,但二者的不同之处在于,他显式地进行了所有梯度计算,以突出概念/数学的清晰性。当然,这么做的缺点也很明显,在每次需要微分一个新函数时,你都要写出它的公式……
估计 David Bourgin 小哥哥在写完这个项目后,机器学习基础已经极其牢固了。最后,David 表示下一步会添加文档和示例,以方便大家使用。
项目总体介绍
这个项目最大的特点是作者把机器学习模型都用 NumPy 手写了一遍,包括更显式的梯度计算和反向传播过程。可以说它就是一个机器学习框架了,只不过代码可读性会强很多。
David Bourgin 表示他一直在慢慢写或收集不同模型与模块的纯 NumPy 实现,它们跑起来可能没那么快,但是模型的具体过程一定足够直观。每当我们想了解模型 API 背后的实现,却又不想看复杂的框架代码,那么它可以作为快速的参考。
文章后面会具体介绍整个项目都有什么模型,这里先简要介绍它的整体结构。如下所示为项目文件,不同的文件夹即不同种类的代码集。
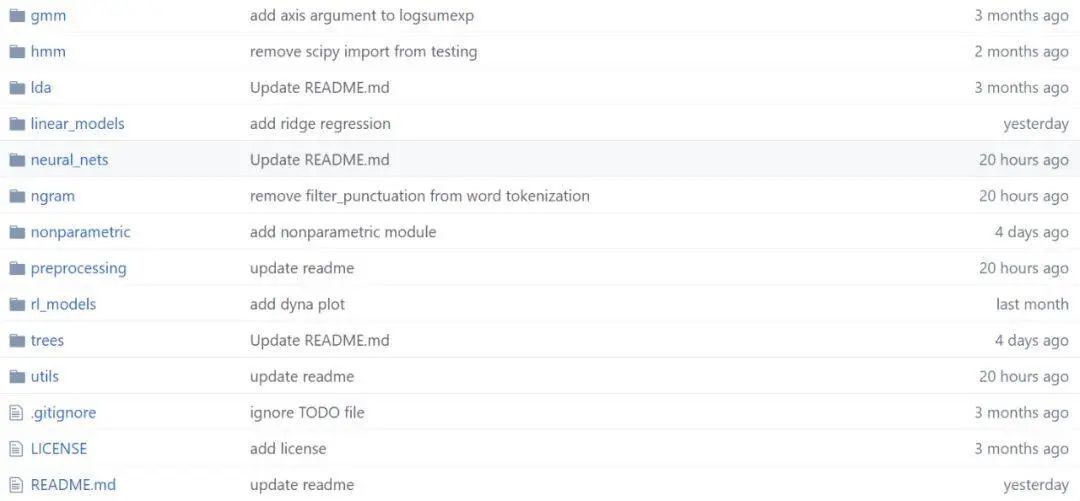
在每一个代码集下,作者都会提供不同实现的参考资料,例如模型的效果示例图、参考论文和参考链接等。如下所示,David 在实现神经网络层级的过程中,还提供了参考论文。

当然如此庞大的代码总会存在一些 Bug,作者也非常希望我们能一起完善这些实现。如果我们以前用纯 NumPy 实现过某些好玩的模型,那也可以直接提交 PR 请求。因为实现基本上都只依赖于 NumPy,那么环境配置就简单很多了,大家差不多都能跑得动。
手写 NumPy 全家福
作者在 GitHub 中提供了模型/模块的实现列表,列表结构基本就是代码文件的结构了。整体上,模型主要分为两部分,即传统机器学习模型与主流的深度学习模型。
其中浅层模型既有隐马尔可夫模型和提升方法这样的复杂模型,也包含了线性回归或最近邻等经典方法。而深度模型则主要从各种模块、层级、、最优化器等角度搭建代码架构,从而能快速构建各种神经网络。
除了模型外,整个项目还有一些辅助模块,包括一堆预处理相关的组件和有用的小工具。
该 repo 的模型或代码结构如下所示:
1. 高斯混合模型
-
EM 训练
2. 隐马尔可夫模型
-
维特比解码
-
似然计算
-
通过 Baum-Welch/forward-backward 算法进行 MLE 参数估计
3. 隐狄利克雷分配模型(主题模型)
-
用变分 EM 进行 MLE 参数估计的标准模型
-
用 MCMC 进行 MAP 参数估计的平滑模型
4. 神经网络
4.1 层/层级运算
-
Add
-
Flatten
-
Multiply
-
Softmax
-
全连接/Dense
-
稀疏进化连接
-
LSTM
-
Elman 风格的 RNN
-
最大+平均池化
-
点积注意力
-
受限玻尔兹曼机 (w. CD-n training)
-
2D 转置卷积 (w. padding 和 stride)
-
2D 卷积 (w. padding、dilation 和 stride)
-
1D 卷积 (w. padding、dilation、stride 和 causality)
4.2 模块
-
双向 LSTM
-
ResNet 风格的残差块(恒等变换和卷积)
-
WaveNet 风格的残差块(带有扩张因果卷积)
-
Transformer 风格的多头缩放点积注意力
4.3 正则化项
-
Dropout
-
归一化
-
批归一化(时间上和空间上)
-
层归一化(时间上和空间上)
4.4 优化器
-
SGD w/ 动量
-
AdaGrad
-
RMSProp
4.5 学习率调度器
-
常数
-
指数
-
Noam/Transformer
-
Dlib 调度器
4.6 权重初始化器
-
Glorot/Xavier uniform 和 normal
-
He/Kaiming uniform 和 normal
-
标准和截断正态分布初始化
4.7 损失
-
交叉熵
-
平方差
-
Bernoulli VAE 损失
-
带有梯度惩罚的 Wasserstein 损失
4.8 激活函数
-
ReLU
-
Tanh
-
Affine
-
Sigmoid
-
Leaky ReLU
4.9 模型
-
Bernoulli 变分自编码器
-
带有梯度惩罚的 Wasserstein GAN
4.10 神经网络工具
-
col2im (MATLAB 端口)
-
im2col (MATLAB 端口)
-
conv1D
-
conv2D
-
deconv2D
-
minibatch
5. 基于树的模型
-
决策树 (CART)
-
[Bagging] 随机森林
-
[Boosting] 梯度提升决策树
6. 线性模型
-
岭回归
-
Logistic 回归
-
最小二乘法
-
贝叶斯线性回归 w/共轭先验
7.n 元序列模型
-
最大似然得分
-
Additive/Lidstone 平滑
-
简单 Good-Turing 平滑
8. 强化学习模型
-
使用交叉熵方法的智能体
-
首次访问 on-policy 蒙特卡罗智能体
-
加权增量重要采样蒙特卡罗智能体
-
Expected SARSA 智能体
-
TD-0 Q-learning 智能体
-
Dyna-Q / Dyna-Q+ 优先扫描
9. 非参数模型
-
Nadaraya-Watson 核回归
-
k 最近邻分类与回归
10. 预处理
-
离散傅立叶变换 (1D 信号)
-
双线性插值 (2D 信号)
-
最近邻插值 (1D 和 2D 信号)
-
自相关 (1D 信号)
-
信号窗口
-
文本分词
-
特征哈希
-
特征标准化
-
One-hot 编码/解码
-
Huffman 编码/解码
-
词频逆文档频率编码
11. 工具
-
相似度核
-
距离度量
-
优先级队列
-
Ball tree 数据结构
项目示例
由于代码量庞大,机器之心在这里整理了一些示例。
例如,实现点积注意力机制:
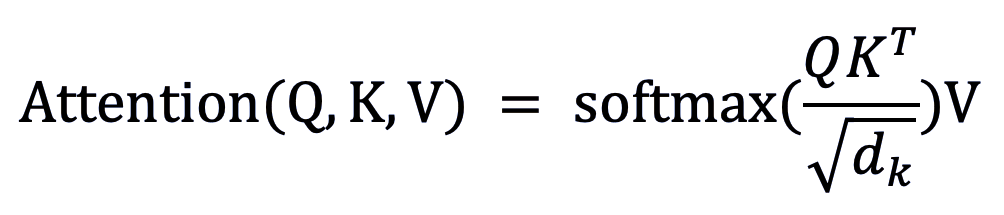
class DotProductAttention(LayerBase):
def __init__(self, scale=True, dropout_p=0, init="glorot_uniform", optimizer=None):
super().__init__(optimizer)
self.init = init
self.scale = scale
self.dropout_p = dropout_p
self.optimizer = self.optimizer
self._init_params()
def _fwd(self, Q, K, V):
scale = 1 / np.sqrt(Q.shape[-1]) if self.scale else 1
scores = Q @ K.swapaxes(-2, -1) * scale # attention scores
weights = self.softmax.forward(scores) # attention weights
Y = weights @ V
return Y, weights
def _bwd(self, dy, q, k, v, weights):
d_k = k.shape[-1]
scale = 1 / np.sqrt(d_k) if self.scale else 1
dV = weights.swapaxes(-2, -1) @ dy
dWeights = dy @ v.swapaxes(-2, -1)
dScores = self.softmax.backward(dWeights)
dQ = dScores @ k * scale
dK = dScores.swapaxes(-2, -1) @ q * scale
return dQ, dK, dV
在以上代码中,Q、K、V 三个向量输入到「_fwd」函数中,用于计算每个向量的注意力分数,并通过 softmax 的方式得到权重。而「_bwd」函数则计算 V、注意力权重、注意力分数、Q 和 K 的梯度,用于更新网络权重。
在一些实现中,作者也进行了测试,并给出了测试结果。如图为隐狄利克雷(Latent Dirichlet allocation,LDA)实现进行文本聚类的结果。左图为词语在特定主题中的分布热力图。右图则为文档在特定主题中的分布热力图。
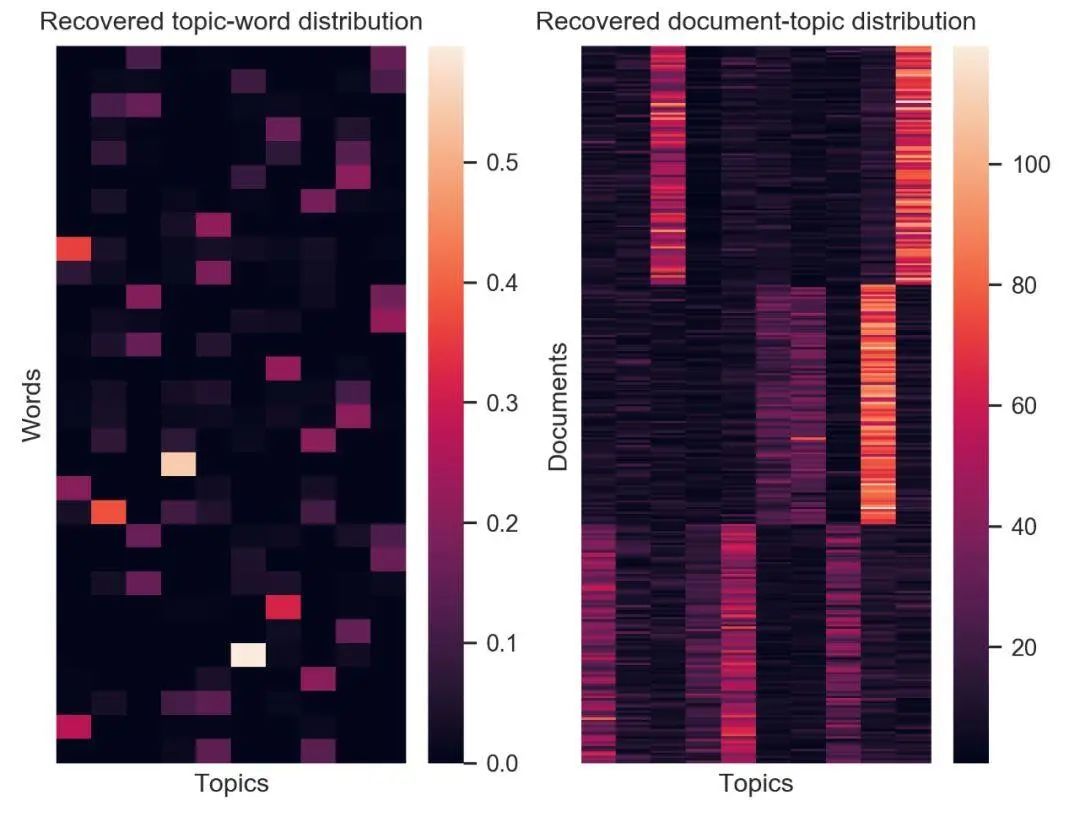
图注:隐狄利克雷分布实现的效果
-
普林斯顿研究员宣称量子计算再获突破2012-10-22 3944
-
普林斯顿研发出世界首枚光子神经形态芯片 以证明其超算能力2016-11-21 857
-
11个机器学习开源项目2017-02-14 2825
-
机器学习可以用来预测多维化学空间中合成反应的性能2018-04-29 5159
-
机器学习初学者最受欢迎的30个开源项目2018-05-08 6955
-
普林斯顿大学与英特尔合作,绘制大脑“地图”2018-08-17 3464
-
2018年值得收藏的30个机器学习案例2018-10-06 11687
-
如何理解深度学习?深度学习的理论探索分析2018-10-03 3703
-
希荻微与普林斯顿大学合作研究下一代芯粒技术供电架构2023-07-21 541
-
机器学习算法入门 机器学习算法介绍 机器学习算法对比2023-08-17 971
-
机器学习有哪些算法?机器学习分类算法有哪些?机器学习预判有哪些算法?2023-08-17 2016
-
普林斯顿仪器为燃烧领域的研究提供一臂之力2024-02-01 520
-
普林斯顿大学联手DARPA研发人工智能芯片2024-03-10 776
全部0条评论

快来发表一下你的评论吧 !

