

信号频谱分析与功率谱密度解析
描述
当我们涉及无线通信、信号处理和电子设备时,信号频谱分析与功率谱密度是两个至关重要的概念。它们帮助我们理解信号的特性、噪声和频率分布,从而优化通信系统、设计滤波器以及进行故障诊断。本文将初步探讨信号频谱分析与功率谱密度,一起理解其在工程和科技领域的应用。
信号频谱分析
信号频谱分析是将信号从时域转换到频域的过程,以便我们可以看清信号在各个频率上的分布情况。频谱图显示信号中各频率分量的强度,帮助我们分析信号的频率成分、调制方式以及可能的噪声。常见的频谱分析方法包括傅里叶变换、快速傅里叶变换(FFT)、小波变换等。
傅里叶变换:解析信号的频域奥秘
傅里叶变换是信号处理领域中的基础概念,它是将信号从时域转换到频域的重要方法。通过傅里叶变换,我们可以揭示信号的频率成分,理解信号的周期性和振幅,从而在许多领域中实现广泛的应用。本文将介绍傅里叶变换的基本原理、应用以及在科学和工程中的重要性。
傅里叶变换的原理
傅里叶变换是一种数学工具,用于将一个时域信号分解为多个不同频率的正弦和余弦波的叠加。它的核心思想是,任何周期性信号都可以由不同频率的正弦和余弦波组合而成。通过傅里叶变换,我们可以获得信号在频域中的频率分布和振幅信息。
傅里叶变换的应用
- 信号分析与滤波 :傅里叶变换可以将信号从时域转换到频域,帮助我们分析信号的频率成分。在滤波中,我们可以选择特定频率范围内的分量,实现去除噪声或突变的效果。
- 图像处理 :傅里叶变换在图像处理中也有广泛应用。将图像进行傅里叶变换后,可以将图像分解为不同频率的分量,实现图像的平滑、锐化等处理。
- 通信系统 :傅里叶变换在通信系统中用于调制和解调信号。它可以将数字信号转换为频域信号,实现信号的传输和恢复。
- 声音处理 :傅里叶变换在音频处理中也有重要应用。将声音信号进行傅里叶变换,可以分析声音的频率成分,实现音频压缩、降噪等处理。
- 科学研究 :傅里叶变换在科学研究中有广泛应用,如天文学、地球物理学等领域。它可以帮助科学家分析复杂的信号数据,揭示隐藏的物理特性。
小结
傅里叶变换是一种强大的信号处理工具,可以将信号从时域转换到频域,揭示信号的频率成分和特性。它在信号、图像、声音、通信等领域都有广泛应用,帮助我们更好地分析、处理和理解数据。了解傅里叶变换的原理和应用,可以为科学研究、工程设计和技术创新提供有力支持。
快速傅里叶变换(FFT):解析频域的神奇算法
快速傅里叶变换(FFT)是一种高效的计算傅里叶变换的算法,它在信号处理、图像处理、通信系统等领域中具有重要的应用。FFT算法的出现极大地提高了傅里叶变换的计算速度,使得我们能够更快地从时域转换到频域,深入分析信号的频率成分和特性。
FFT的基本原理
傅里叶变换是一种将信号从时域转换到频域的方法,但传统的傅里叶变换算法的时间复杂度为O(n^2),对于大规模的信号数据计算效率较低。FFT算法通过分治和迭代的思想,将复杂度降低到O(n log n),极大地提高了计算速度。
FFT的基本思想是将信号分解为不同频率的正弦和余弦波,然后将这些波的频率分量合并计算,从而得到信号的频谱。FFT算法通过将信号分解为多个子问题,逐层计算频谱,最终得到完整的频谱信息。
FFT的应用领域
- 信号分析与滤波 :在信号处理中,FFT可以帮助我们分析信号的频率成分。通过将信号转换到频域,我们可以选择特定频率范围内的分量,实现滤波和降噪的效果。
- 通信系统 :在通信系统中,FFT用于调制和解调信号。它可以将数字信号转换为频域信号,实现信号的传输和恢复。
- 图像处理 :FFT在图像处理中也有广泛应用。通过对图像进行FFT变换,可以分析图像的频率特性,实现图像增强、去噪等处理。
- 音频处理 :在音频处理领域,FFT可以帮助我们分析音频信号的频率成分,实现音频压缩、均衡等处理。
- 科学研究 :FFT在科学研究中具有重要作用,如天文学、地球物理学等领域。它可以帮助科学家分析复杂的信号数据,揭示隐藏的物理特性。
FFT的实现与工具
FFT算法有多种实现方式,包括蝶形算法、快速拉宾算法等。在实际应用中,有许多开源工具和库可以帮助我们进行FFT计算,如NumPy、MATLAB等。
快速傅里叶变换是一项强大的信号处理技术,通过高效的计算方法,可以从时域转换到频域,揭示信号的频率分布和特性。它在多个领域中都有重要应用,帮助我们更好地理解和处理各种信号数据。
小波变换:从信号到频谱的多尺度分析
在信号处理领域,小波变换是一种强大的工具,用于将信号从时域转换到频域,并在不同尺度上进行分析。与传统的傅里叶变换或快速傅里叶变换不同,小波变换允许我们同时观察信号的时间和频率特性,提供了更详细和全面的信息。本文将深入介绍小波变换的原理、应用以及其在现代科学和工程中的重要性。
小波变换的原理
小波变换使用一组称为小波基函数的函数族,这些函数在时域和频域上都具有局部性质。通过对信号进行小波变换,我们可以在时间和频率上同时获取信息,而不像傅里叶变换那样仅仅提供频率信息。小波基函数在时域上的伸缩和平移可以让我们捕捉到信号中不同尺度的特征。
小波变换的应用
- 信号分析与处理 :小波变换在信号处理中广泛应用,可以识别信号中的瞬态、脉冲、周期性等特征。通过对不同尺度下的小波系数进行分析,我们可以更好地了解信号的结构。
- 图像处理 :小波变换可以应用于图像处理,用于边缘检测、去噪、图像压缩等。由于小波变换的多尺度特性,它可以捕捉图像中不同大小的特征。
- 声音处理 :小波变换在音频处理中有重要应用,可以分析声音的谐波、噪声、共振等特征,有助于音频压缩、降噪以及音频特征提取。
- 振动分析 :在机械工程和结构健康监测中,小波变换可以帮助分析机械振动信号的频率分量,用于故障诊断和状态监测。
- 金融分析 :小波变换可用于分析金融时间序列数据,揭示不同时间尺度上的市场波动情况,以及趋势和周期性变化。
小波变换与傅里叶变换的比较
尽管小波变换在许多应用中非常强大,但傅里叶变换仍然在某些情况下更加适用。以下是两者之间的比较:
- 分辨率 :小波变换具有多尺度分析的能力,可以捕捉信号的局部特征。傅里叶变换则提供信号的全局频率信息。
- 计算效率 :小波变换的计算相对复杂,尤其是连续小波变换。傅里叶变换的快速算法(FFT)可以在计算上更高效。
- 稳定性 :小波变换对信号中的突变和瞬态有更好的稳定性,而傅里叶变换可能会产生频谱泄漏。
小结
小波变换是信号处理领域中的重要工具,通过多尺度分析提供了更全面的信号信息。它在信号、图像、声音、振动等领域都有广泛应用,帮助我们更好地理解和处理复杂的数据。了解小波变换的基本原理和应用,可以为工程、科研和技术创新提供强大的支持。
功率谱密度:揭示信号能量分布的重要工具
功率谱密度是信号处理中的一个关键概念,它描述了信号在不同频率上的能量分布情况。通过分析信号的功率谱密度,我们可以深入了解信号的频率成分和能量分布,从而在许多领域中做出更准确的判断和决策。
功率谱密度的定义
功率谱密度是一个表示信号在不同频率上的功率分布的函数。在频谱分析中,我们通常使用傅里叶变换来将信号从时域转换到频域,然后计算信号的功率谱密度。功率谱密度可以告诉我们在不同频率范围内信号的功率大小。
为什么需要功率谱密度?
功率谱密度在许多应用中都扮演着重要的角色:
- 信号特征分析 :通过分析信号的功率谱密度,我们可以了解信号的频率成分,从而判断信号的类型、周期性等特征。
- 通信系统 :在通信系统中,功率谱密度可以帮助我们合理规划信道带宽和频率分配,以提高通信质量和效率。
- 噪声分析 :功率谱密度可以帮助我们分析信号中的噪声分布情况,进而选择合适的滤波方法来降低噪声影响。
- 振动分析 :在振动领域,功率谱密度可以用来分析结构的振动特性,帮助工程师检测结构的异常和问题。
计算功率谱密度
计算功率谱密度需要以下步骤:
- 获取信号数据 :首先,需要获取要分析的信号数据,可以是时间域的采样数据。
- 进行傅里叶变换 :将信号数据进行傅里叶变换,将信号从时域转换到频域。
- 计算信号功率 :计算每个频率分量上的信号功率,通常是对傅里叶变换结果的幅值平方。
- 绘制功率谱密度图 :将不同频率分量的功率绘制成图表,可以是柱状图或曲线图,展示信号在不同频率上的能量分布情况。
应用案例
在无线通信中,功率谱密度可以帮助确定信号在频域上的占用情况,从而避免不同信号之间的干扰。在音频处理中,功率谱密度可以帮助我们分析音频信号的频谱特性,用于音频编码和解码。
功率谱密度是一个有力的工具,能够帮助我们深入了解信号在频率域上的特性和能量分布情况。在信号处理、通信、工程等领域,它都具有广泛的应用价值,帮助我们做出更准确的分析和决策。
python示例
频谱
示例代码:
import numpy as np
import matplotlib.pyplot as plt
# 生成一个信号,例如一个包含两个频率成分的正弦波
fs = 1000 # 采样率
t = np.linspace(0, 1, fs, endpoint=False)
freq1 = 50 # 第一个频率成分
freq2 = 150 # 第二个频率成分
signal = np.sin(2 * np.pi * freq1 * t) + np.sin(2 * np.pi * freq2 * t)
# 使用快速傅里叶变换计算信号的频谱
fft_result = np.fft.fft(signal)
freqs = np.fft.fftfreq(len(fft_result), 1/fs)
magnitude = np.abs(fft_result)
# 绘制原始信号和频谱
plt.figure(figsize=(10, 6))
plt.subplot(2, 1, 1)
plt.plot(t, signal)
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.title('Original Signal')
plt.subplot(2, 1, 2)
plt.plot(freqs, magnitude)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnitude')
plt.title('Spectrum')
plt.tight_layout()
plt.show()
输出:
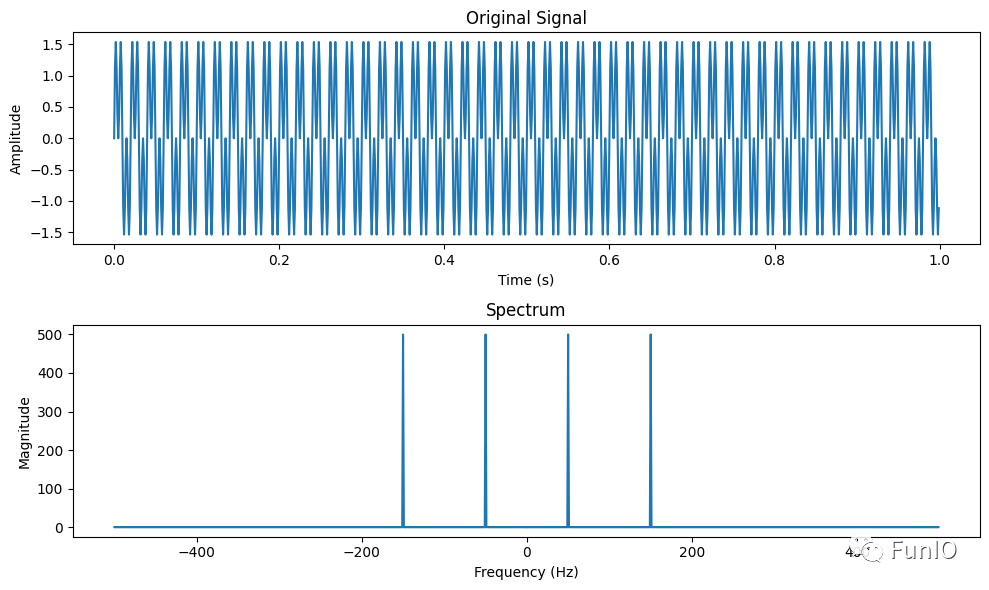
python频谱分析示例
功率谱
示例代码:
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
# 生成一个示例信号(正弦波加噪声)
fs = 1000 # 采样率
t = np.arange(0, 10, 1/fs) # 时间向量
freq = 50 # 正弦波频率
signal_data = np.sin(2*np.pi*freq*t) + 0.5*np.random.randn(len(t))
# 计算功率谱密度
frequencies, power_density = signal.welch(signal_data, fs, nperseg=1024)
# 绘制功率谱密度图
plt.figure(figsize=(10, 6))
plt.semilogy(frequencies, power_density)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Power Density')
plt.title('Power Spectral Density')
plt.grid()
plt.show()
输出:
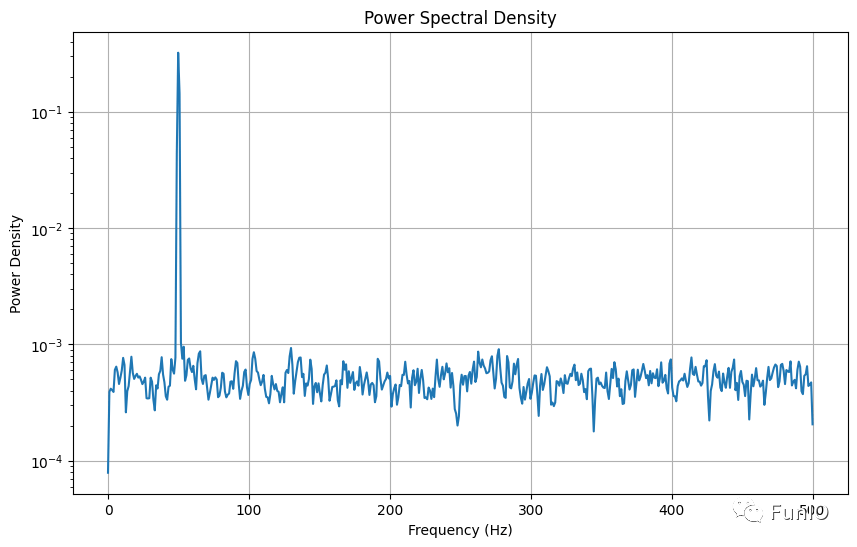
python功率谱分析示例
信号频谱分析与功率谱密度在多个领域有重要应用:
- 通信系统设计 :在通信系统中,了解信号频谱分布有助于选择合适的调制方式和频率分配,以最大化信号传输效率。
- 无线电频谱管理 :在无线电频谱管理中,监测各频段的信号功率谱密度可以避免频段之间的干扰。
- 信号处理与滤波器设计 :根据信号的功率谱密度特点,设计合适的滤波器以去除噪声或选择特定频率分量。
- 噪声分析 :功率谱密度分析有助于识别信号中的噪声成分,并估计其影响。
- 天文学与地震学 :在这些领域,频谱分析帮助科学家研究天体和地震信号的特性。
- 信号故障诊断 :通过分析信号的频谱分布,可以识别信号中的异常或故障。
总结
信号频谱分析与功率谱密度是理解信号特性、优化通信系统和进行故障诊断的关键工具。通过将信号从时域转换到频域,我们可以获得信号在不同频率上的分布情况,从而更好地理解信号的性质。在现代无线通信、信号处理和工程领域,频谱分析与功率谱密度的应用无处不在,为我们带来了许多技术和科学的突破。
-
7.5 GHz!!!鼎阳科技重磅发布SSA3000X-R系列实时频谱分析仪2019-12-19 2298
-
声音数据的频谱分析2016-05-14 5038
-
什么是实时频谱分析仪2022-09-01 50425
-
信号频谱分析和测试2009-06-22 6544
-
什么是数据通信的功率谱密度2010-03-17 6992
-
labview FFT分析信号频谱幅度谱和相位谱实例2017-02-28 6684
-
周期信号的频谱分析实验2017-12-06 1754
-
如何计算噪声的功率谱密度?2023-09-19 11375
-
单频信号的频谱分析2023-10-16 1648
-
请问ADS里如何仿真得到时域信号的功率谱密度?2023-10-20 3154
-
普源RSA5000系列频谱分析仪介绍2023-12-01 1181
-
频谱分析仪和网络分析仪的区别2024-05-08 2129
-
频谱分析仪在卫星接收中的应用2024-05-14 1607
-
频谱分析仪是干什么用的 频谱分析仪和示波器的区别2024-05-31 2287
-
Keysight 频谱分析仪(信号分析仪)2024-09-12 1860
全部0条评论

快来发表一下你的评论吧 !

